1. Introduction
The diffusion of heat and of mass can be treated in a similar fashion by solving the diffusion equation with appropriate boundary conditions. For one dimensional heat flow the diffusion equation becomes
![]()
where
a is the thermal diffusivity and T(x,t) is the temperature at time t at a distance x from a suitable origin. The object of this experiment is to determine the thermal diffusivity a of each of the three strips (X,Y and Z), given that the appropriate solution for the diffusion equation for the temperature T(x,t) at a distance x from a heat source after a time is given by:![]()
where A and B are constants and erf (x) is defined as
2. Experimental Procedure
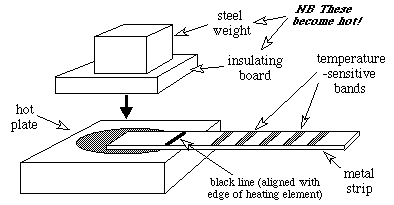
Experimental arrangement for study of diffusional heat flow
a) Ensure heater controller is set to position 2 and has been on for at least 30 minutes.
b) While strip is cold, measure the distances of each of the temperature indicating bands from the black line on the strip indicating the end of the heating element.
c) Set timer to zero.
d) Using the insulating gloves or the tongs to raise a corner of the insulating sheet, place metal strip X between the hot-plate and the weighted insulating sheet so that the black line on the strip is aligned with the edge of the heating element.
e) Immediately start the timer.
f) Observe the liquid crystal temperature-indicating bands and record the times as the temperatures are reached and the colours change:
either from yellow to orange (for a temperature of 50 šC)
or from red to black (for the remaining temperatures).
g) Estimate the temperature of the heating element using a thermocouple, keeping the metal strip in position.
h) Using the insulating gloves or the tongs if required, remove the metal strip from the hot-plate and place on the metal sheet provided (not on the bench).
i) Carry out the analysis outlined in §3.
j) Repeat the operation for both strips Y and Z.
3. Analysis of Data
i) Plot a graph of distance versus ˆ time for each of the five temperatures on the liquid crystal temperature-indicating bands. Both axes on the graph should begin at zero.
ii) By using suitable boundary conditions, derive expressions in terms of temperature for the constants A and B in the equation provided. Note that erf (0) = 0 and erf (
•) = l.iii) Using the values of the constants obtained, determine the thermal diffusivity of the material from each of the gradients of the lines plotted. Values of the error function are given in the Data Book. Would you expect, and do you see, a systematic variation in
a?4. Discussion
The metallographic mounts (X, Y and Z) are of polished sections of the strips prior to rolling. Examine the sections and discuss whether the relative values of thermal diffusivity can be explained in terms of the observed microstructures.
Explain briefly whether or not values of
i) diffusion coefficient and
ii) electrical conductivity
for the three materials would be expected to follow a similar pattern to the values of thermal diffusivity.
For strip X describe and account for the colours observed in the section which had been heated.
H. Bhadeshia, Michaelmas Term 2000