Quantitative modelling tools for the design of Ni-base superalloys
F. Tancret
University of Cambridge
Department of Materials Science and Metallurgy
Pembroke Street - Cambridge CB2 3QZ
United Kingdom
Biography: The author is a Materials Engineer (ISMRA - ENSI Caen), Doctor of the University of Caen, France, and is presently a Research Associate at the University of Cambridge.
His main activities have been in the fields of process development of fiber-reinforced organic matrix composites, thermomechanical characterisation and modelling of ceramics, and modelling and design of nickel-base superalloys.
SYNOPSIS
The Department of materials Science and Metallurgy of the University of Cambridge, UK, makes a wide use of modern modelling techniques as tools for the design of new nickel-base superalloys for specific applications -aeroengines, power-plants... These techniques range from physically-based strengthening models, to neural networks and Gaussian processes -able to model the mechanical behaviour of a whole category of alloys as a function of composition and processing parameters-, phase diagram simulation, and finite element modelling and optimisation of elaboration processes.
INTRODUCTION
Nickel-base superalloys are widely used in aeroengine components, and become used in an increasing number of high-temperature applications, such as power-plants, chemical engineering, automotive industry, etc. Typical alloy development procedures are usually very long, and new superalloys have often been investigated by the "try-and-test" method, by making and testing tens or hundreds of different variants. Processing these alloys also need long and laborious development stages. Consequently, designing a novel alloy is generally a matter of several years of expensive experiments.
In the past years, the Department of Materials Science and Metallurgy of the University of Cambridge has developped and used quantitative modelling techniques to predict the properties and to optimise the processing of nickel-base superalloys, and used them as tools for the design of "made-to-measure" novel alloys for specific applications. This bunch of tools include physically-based models, non-linear regression analyses such as neural networks and Gaussian processes, phase diagram simulations, and finite element modelling. Models concern mechanical properties, g/g’ lattice misfit, phase formation, composition and stability, grain size, crystal growth...
The aim of this paper is to review briefly those modelling techniques and their use as tools for the quantitative design of new nickel-base superalloys.
PHYSICAL MODELS
Nickel-base superalloys are essentially mixtures of g’ intermetallic precipitates in a g matrix, the latter being strengthened by solute atoms such as Cr, Co, Mo, W... Solid solution theory has been used and developped to solve the problem of multi-component strengthening as a function of temperature, using the Feltham equation, a trough model in which dislocations reside in energy wells. The model has been successfully applied to the case of binary Ni-Cr solid solutions, ternary alloys, and several commercial solid solution strengthened nickel-base superalloys [1].
NEURAL NETWORKS AND GAUSSIAN PROCESSES
Many alloy properties are so complex in their dependance on material characteristics that there are no theories available to make generalised quantitative predictions. Neural networks and Gaussian processes are able to perform multi-dimensional non-linear empirical regressions, and represent methods for the quantitative recognition of patterns in data, without any a priori on the nature of the relationship between input and output variables. They can model relationships of almost any complexity. These softwares are implemented within a statistical Bayesian framework, which helps in the determination of the relevance of individual inputs, and in providing meaningful predictive error bars.
1 - Mechanical properties
a) Tensile properties
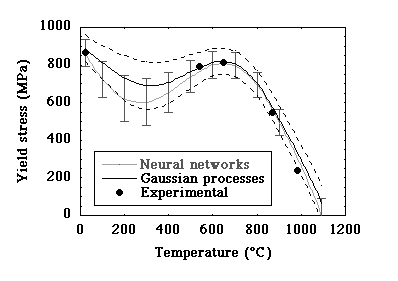
The tensile properties of nickel-base superalloys have been modelled using both neural networks [2] and Gaussian processes [3] as a function of chemical composition (Ni, Cr, Co, Mo, W, Ta, Nb, Al, Ti, Fe, Mn, Si, C, B, Zr) and of test temperature in the range 21-1093 °C. The analysis is based on published data. The models were successfully submitted to a variety of metallurgical tests. For example, they were able to predict correctly the influence of g’-forming (Al, Ti, Nb) and of solution strengthening elements (Mo, W) on the yield stress of Ni-base alloys. Also, the peak effect in the variation of yield stress with temperature, resulting from the competition between the softening g matrix and the hardening g’ precipitates, is well predicted by both models (figure 1).

Figure 1
: Neural network and Gaussian processes predictions of the yield stress of a Nimonic 115 superalloy as a function of temperature.b) Fatigue crack growth
A neural network has been used to model fatigue crack growth rates in nickel-base superalloys as a function of 51 input variables, including chemical composition, temperature, grain size, heat treatment, the stress intensity range DK, frequency, load waveform, atmosphere, R-ratio, yield stress... The analysis was conducted on published data.
The model, unlike any experimental approach, could be used to study the effect of each variable in isolation. For example, it was verified that an increase in grain size should lead to a decrease in fatigue crack growth rate. This cannot be done experimentally since grain size is controlled by heat treatment, which influences other microstructural parameters. Many other metallurgical trends have been revealed [4].
The method has been used in the context of a Rolls-Royce disc alloy development programme.
c) Creep rupture
Creep rupture resistance is a crucial property in high temperature applications. The creep rupture stress of nickel-base superalloys has been modelled by neural networks [5] and Gaussian processes [6] as a function of many variables, including composition, mechanical and heat treatments, test temperature, and lifetime. Once more, several metallurgical trends have been quantitatively predicted by the models. For example, the Gaussian processes model is able to predict accurately the relation between the creep rupture stress of an Inconel 939 superalloy and its lifetime at 870 °C (figure 2).
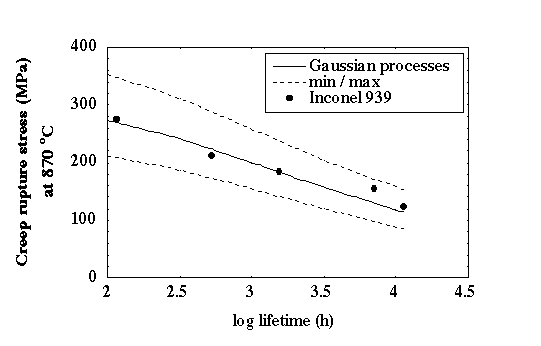
Figure 2
: Gaussian processes modelling of the relation between the creep rupture stress of an Inconel 939 superalloy and its lifetime at 870 °C.2 - g/g’ lattice misfit
Designing Ni-base superalloys with a small or slightly negative g/g’ lattice misfit is of critical importance for creep resistance, because the interface energy and structure affect the dislocation climbing creep mechanism, and the rafting phenomenon in single crystals (stress-oriented coarsening of g’). Therefore, neural networks [7] and Gaussian processes models have been developped to predict the g/g’ lattice misfit as a function of composition and temperature, and have been used as tools in the design of new alloys for aeroengines and power-plant applications.
PHASE DIAGRAM SIMULATION
Neural networks or Gaussian processes models alone are not always confident when making predictions, since they are sometimes asked to interpolate or extrapolate in regions of the database where data are widely scattered. In these regions, mechanical properties predictions might be wrong due to a change in phase equilibria, which is ignored by regression models.
Consequently, thermodynamical simulation softwares are often used in alloy design procedures to predict phase diagrams. In the case of nickel-base superalloys, they are very useful to predict the absence (rather than the presence!) of undesirable phases such as TCP (s, m...) or a phases (Cr, W...) [8]. Also, they are of capital importance in the design of elaboration processes [6], in order to predict the melting point, the solidification range, and the forging window (the g’-free region between the g’ solvus and the solidus). Finally, designing the heat treatment requires a knowledge of the domains of existence of g’, carbides, and borides. An example of phase formation in a recently designed Ni-Cr-W-Al-Ti-Fe-C-Si-B superalloy is presented in figure 3.
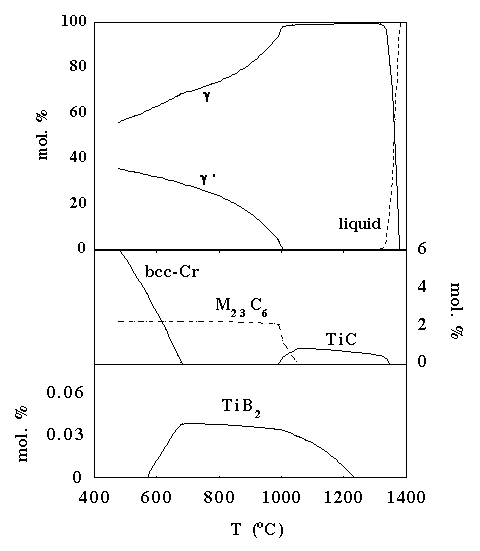
Figure 3
: Thermodynamical simulation of equilibrium phase formation in a newly developped superalloy as a function of temperature.FINITE ELEMENT MODELLING
Finite element modelling of processing conditions is very important in that it reduces considerably the process development time and cost, through a limitation in the number of industrial-scale experiments.
Those techniques are being used at the University of Cambridge to model superalloy single crystal growth techniques and to optimise elaboration parameters such as temperature, temperature gradient, growth rate, shape of the grain selector, etc.
Programmes are presently in progress to model temperature, strain and strain rate effects on recrystallisation and on the cracking phenomenon during the forging process. The former project also makes use of a neural network able to model the grain size evolution as a function of deformation parameters.
EXAMPLE AND CONCLUSIONS
The modelling techniques used in the Department of Materials Science and Metallurgy of the University of Cambridge are useful tools to design new "made-to-measure" nickel-base superalloys for specific applications. They range from physical metallurgy models to thermodynamical simulation, neural networks, Gaussian processes, and finite element modelling of elaboration processes. They are often used as complements of each other in the whole design procedure, and have led to a considerable shortening of the development stage of promising superalloys.
As an example, a new creep-resistant alloy for power-plant applications has been designed on the basis of its predicted mechanical properties (Gaussian processes modelling of the yield stress, UTS, tensile ductility, creep rupture stress and ductility), a low g/g’ lattice misfit (Gaussian processes), and the absence of undesirable phases at service temperature (thermodynamical simulation). Phase diagram simulation has also been used as a guide to design the heat treatment. This weldable and forgeable Ni-Cr-W-Al-Ti-Fe-C-Si-B alloy should have a creep rupture life of 100000 hours at 750 °C under a stress of 100 MPa, with a significant price reduction compared to existing Ni-base superalloys with similar properties [6].
DISSEMINATION
A lot of the work, data and models are available on the Internet from the Materials Algorithms Project site:
https://www.phase-trans.msm.cam.ac.uk/map
ACKNOWLEDGEMENTS
The author is extremely grateful to Dr. H.K.D.H. Bhadeshia for permanent encouragement and useful discussions, to Pr. C.J. Humphreys and Dr. R.C. Reed for the provision of facilities within the Rolls-Royce University Technology Centre, and to Dr. D.J.C. MacKay for the development of powerful modelling softwares. He would like to thank the Engineering and Physical Sciences Research Council for funding his work; and Corus, Special Metals, ABB Alstom Power, Rolls-Royce and Mitsui Babcock Energy Limited for partnership.
REFERENCES
[1] H.A. Roth, C.L. Davis and R.C. Thomson, Metallurgical and Materials Transactions, 28A (1997) 1329-1335.
[2] J. Warde and D.M. Knowles, ISIJ International, 39(10) (1999) 1006-1019.
[3] F. Tancret, H.K.D.H. Bhadeshia and D.J.C. MacKay, ISIJ International, 39(10) (1999) 1020-1026.
[4] H. Fuji, D.J.C. MacKay and H.K.D.H. Bhadeshia, ISIJ International, 36(11) (1996) 1373-1382.
[5] H. Fuji, D.J.C. MacKay, H.K.D.H. Bhadeshia, H. Harada and K. Nogi, Journal of the Japan Institute of Metals, 63(7) (1999) 905-911.
[6] F. Tancret, H.K.D.H. Bhadeshia and D.J.C. MacKay, Key Engineering Materials, 171-174 (2000) 529-536.
[7] S. Yoshitake, V. Narayan, H. Harada, H.K.D.H. Bhadeshia and D.J.C. MacKay, ISIJ International, 38(5) (1998) 495-502.
[8] R.C. Reed, M.P. Jackson and Y.S. Na, Metallurgical and Materials Transactions A, 30(3) (1999) 521-533.