Master of Philosophy Course Modelling of Materials

Abstract

The steels used in the power generation industry are almost always given a severe tempering heat-treatment before they enter service. This would, in most contexts, give them a highly stable microstructure which is close to equilibrium. In fact, they undergo many changes over long periods of time. This article is a review of some of the methods which exploit the changes in order to estimate the life that remains in alloys which are only partly exhausted.

INTRODUCTION

Many of the safety-critical components in power plant are made of steels developed to resist deformation when used in the range 480-565 ^oC and 15-90 MPa. They are expected to serve reliably for a period of about 30 years, giving a maximum tolerable creep strain rate of about 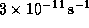(approximately two percent elongation over the 30 years). The design stress must be set to be small enough to prevent creep rupture over the intended life of the plant.

The steels are able to survive for such long periods because the operating temperature is only about half of the absolute melting temperature, making the migration of atoms very slow indeed. Creep therefore depends on the ability of dislocations to overcome obstacles with the help of thermal energy. The obstacles are mainly carbide particles which are dispersed throughout the microstructure.

Suppose that the microstructure and the operating conditions do not change during service. The accuracy with which component life might then be predicted would depend only on the quality of the experimental data. The so-called safety factors common in design could then be greatly reduced with obvious benefits. Of course, this never happens in practice; the steels are always heterogeneous and the service conditions vary over a range of scales and locations. The design life is therefore set conservatively to account for the fact that measured creep data follow a Gaussian distribution with a significant width. In spite of this, experience has shown that decommissioned plant could have been kept in service without sacrificing safety. To take advantage of this observation requires methods for the reliable estimation of the remaining life. The techniques used for this purpose are summarised in Table 1. Of the properties listed, no single measurement is comprehensive enough to describe the steel with all requisite completeness. However, the present survey is confined to just two topics, damage parameters and hardness changes. It is recognised that the implementation of a life-extension procedure must be based on much wider considerations backed by more frequent inspections.

Table 1: Methods used in the estimation of remaining life.

Property	References
Damage summation	Evans, 1984 [1]
Hardness	Goto, 1984 [2]
Tensile test	Cane and Williams, 1987 [3]
Interparticle spacing	Askins and Menzies, 1985 [4]
Cavitation parameter	Gooch, 1989 [5]
Number density of cavities	Dyson and McLean, 1972 [6]
Fraction of cavities	Walker and Evans, 1970 [7]
Impact toughness	Wignarajah et al. 1990 [8]

DAMAGE SUMMATION

A satisfactory way of representing creep damage (C) is to use a parameter () which is normalised by its value at failure (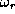). The magnitude of 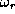will depend on the precise values of stress 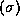, temperature (T) and any other variable which influences the creep process. Since these variables are not necessarily constant, the extent of damage is often written [1,9]


is typically the time or the creep strain. Failure occurs when the sum achieves a value of unity.

Evans [1] argues that it is more appropriate to use the strain rather than the time, since the latter is not considered as a state variable. In the context of thermodynamics, the state of a system can in principal be specified completely by a number of state variables (such as temperature, pressure) such that its properties do not depend at all on the path by which those variables were achieved. This clearly cannot be the case even for the creep strain. This is because the extent of damage is expected to depend on the path by which a given value of strain is achieved, for example, whether the strain is localised at grain boundaries or uniformly distributed. This necessarily means that the above equation is an approximation; as Evans states, it should be a reasonable approximation if the mechanism of creep does not change between the components of the summation. Thus, Cane and Townsend [10] conclude that the use of the life fraction rule in taking account of temperature variations is more justified than for variations in stress. This is because for the latter case, the dislocation networks become finer (relative to the carbide spacings) at large stresses. The network nodes then do not coincide with carbide particles, thus changing the mechanism of deformation. This is not the case with variations in temperature because the dislocation network then scales with the particle spacing. The failure of the life fraction rule is sometimes accommodated by empirically setting the limiting value of C to some positive value which is not unity.

HARDNESS, INTERPARTICLE SPACING

The hardness can be used as an indicator for the state of the steel in its life cycle. Changes in hardness occur due to recovery, coarsening of carbide particles, and recrystallisation. All creep-resistant power plant steels are severely tempered before they enter service. They are therefore beyond the state where secondary hardening is expected and the hardness can, during service, be expected to decrease monotonically. In these circumstances, an Avrami equation adequately represents the changes in hardness,

where t is the time, 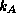and n rate constants and 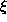is given by

where 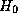is the initial hardness, 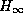is its hardness at the end of useful life and 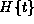the hardness at time t.

The hardness at the point where the microstructure is exhaustively annealed is likely to be around 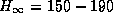HV for most power plant steels. Its main components include the intrinsic strength of iron and solid solution strengthening. The starting hardness is likely to be in the range 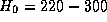HV. Therefore, all that can be expected is a change in hardness of about 30-70 HV over a period of some 30 years. Thus, Roberts and Strang [11] have shown that the hardness can decrease by about 20% in the stressed regions of long-term creep test specimens; this is consistent with an approximately 25% reduction found by Maguire and Gooch [12]. Figure 1 shows the nature of the changes in hardness to be expected typically, as reported by Maguire and Gooch [12] for a 1CrMoV steel which was tempered at 700 ^oC for 18 h prior to the ageing at temperatures in the range 600-640 ^oC.

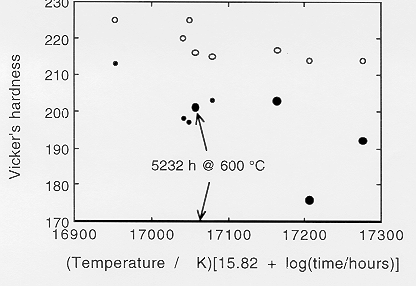Figure 1: Changes in the hardness of a 1CrMoV steel during ageing in the temperature range 600-640. The open circles are data from the grips of a creep test specimen, and the filled circles represent measurements from the gauge length. Data from Maguire and Gooch.



Precipitates impede the motion of dislocations and any strength in excess of 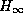is often related to the spacing (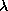) between the particles (Cane, 1986, 1987):

where it is assumed that in order to be consistent with coarsening theory.

It is well known that differences in hardness develop in the grip and gauge length of a creep test specimen (Figure 1). The strain in the gauge length leads to accelerated softening. In fact, the hardness reduction that occurs in the gauge length is roughly proportional to that in the grip [12]. Tack [13] have therefore taken H to be a function of strain:

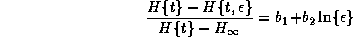
where 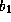and 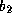are empirical constants. This illustrates the fact that hardness is a crude indicator of remaining life. Furthermore, it's ability to account for creep damage in the form of voids is not represented in any theory. Hardness tests can therefore only serve a useful purpose in the regime of steady-state creep, before the onset of gross damage. This is evident from where it is seen that specimens with the same hardness are at different life-fractions. There is a further complication, that the hardness of welded regions is likely to be inhomogeneous even when the welds are made with matching compositions. The potential location of failure is then difficult to identify since creep ductility, creep strength and creep strain may vary with position. The weld metal always has a larger oxide content than the parent steel, and hence has a lower creep ductility. It cannot therefore be assumed that failure will always occur in the softest part of the joint. A harder weld may be needed to ensure the same rupture life as the parent steel (Figure 2).

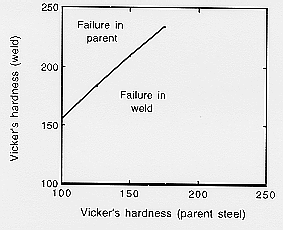Figure 2: Data for 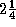Cr1Mo steel and matching weld metal. The curve represents the locus of all points along which the weld metal and parent metal have equal rupture lives. Note that for a given life, the weld must be harder than the parent steel (after Tack, [13]).



The hardness can be related inversely to the spacing between precipitate particles; this is illustrated in Figure 3 for a 1Cr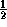Mo steel [4]. The spacings are typically measured using transmission electron microscopy at a magnification of about 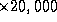with approximately 100 fields of view covering 30 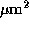taken at random. The actual measurement involves counting the number of particles per unit area (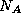) and it is assumed that 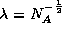. The amount of material examined in any transmission microscope experiment is incredibly small, so care has to exercised in choosing representative samples of steel. In some cases, the microstructure may be inherently inhomogeneous. One example is the 12Cr and 9Cr type steels where there is a possibility of regions of delta-ferrite where the precipitation is quite different from the majority tempered martensite microstructure.

Obviously, hardness tests are much simpler to conduct when compared with the effort required to properly measure particle spacings. A further complication is that there is frequently a mixture of many kinds of particles present, some of which continue precipitation during service whereas others dissolve. Thus, Battaini [14] found that in a 12CrMoV steel, precipitation continues to such an extent during service that there is a monotonic decrease in 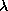. In fact, the distribution of particles was bimodal with peaks at 30 nm and 300 nm diameters. It is strange that they were only able to correlate the hardness against the changes in the coarser particles. For another steel (12CrMoVW), Battaini found an even more complex variation in the interparticle spacing with a maximum value in 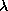for the coarse particles.

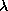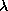It should be emphasised that the standard error in measurements is quite large, frequently larger than the variations observed. Given the difficulties of interpretation, and the experimental error, it is unlikely that measurements can be used as a satisfactory general measure of remaining life. The data can nevertheless be of use in the design of physically based creep models.


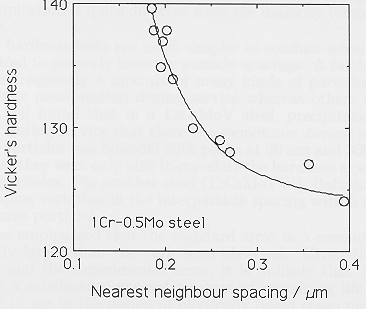
Figure 3: The hardness as a function of the near neighbour spacing of carbides following creep tests at 630 ^oC for a variety of time periods. After Askins and Menzies, 1985 [4].




CONCLUSIONS

The present work is by no means a comprehensive review of the available literature. There is a vast array of methods available for the assessment of remaining life in power plant steels. Of these, the use of damage parameters and hardness measurements have been the subject of this review. Although there are difficulties of interpretation and considerable uncertainties in the data, both of these parameters can, with care, be used as approximate indicators of remanent life.

REFERENCES

[1] H. E. Evans: Mechanisms of Creep Fracture, Elsevier Applied Science Publishers, Essex, England (1984)

[2] T. Goto: Creep and fracture of engineering materials and structures, Swansea, Pineridge Press, (1984) 1135.

[3] B. J. Cane and J. A. Williams: International Materials Reviews 32 (1987) 241-262.

[4] M. C. Askins and K. Menzies: Unpublished work, referred to in Gooch and Townsend, (1987) 1985

[5] D. J. Gooch, M. S. Shammas, M. C. Coleman, S. J. Brett and R. A. Stevens: Proc. Conf. Fossil Power Plant Rehabillitation, Cincinnati, Ohio, ASM International, Ohio (1989) Paper 8901-004.

[6] B. F. Dyson and D. McLean: Metal Science 6 (1972) 220.

[7] G. K. Walker and H. E. Evans: Metal Science 4 (1970) 155.

[8] S. Wignarajah, I. Masumoto and T. Hara: ISIJ international 30 (1990) 58-63.

[9] E. L. Robinson: Trans. Am. Soc. Mech. Engrs. 74 (1952) 777.

[10] B. J. Cane and R. D. Townsend: CEGB report TPRD/L/2674/N84, Leatherhead, Surrey (1984)

[11] B. W. Roberts and A. Strang: Refurbishment and Life Extension of Steam Plant, Institution of Mechanical Engineers, London (1987) 205-213.

[12] J. Maguire and D. J. Gooch: Proc. Int. Conf. Life Assessment and Extension, The Hague, (1988).

[13] A. J. Tack, J. M. Brear and F. J. Seco: Creep: Characterisation, Damage and Life Assessment, eds D. A. Woodford, C. H. A. Townley and M. Ohnami, ASM International, Ohio, U.S.A. (1992) 609-616.

[14] P. Battaini, D. D'Angelo, G. Marino and J. Hald: Creep and Fracture of Engineering Materials and Structures, Institute of Metals, London (1990) 1039-1054.

Department of Materials Science and Metallurgy, University of Cambridge, Pembroke Street, Cambridge CB2 3QZ, U.K.

. . . . . . . . . . . .