An interstitial solute diffuses through a 0.25 mm thin foil of nickel at a steady rate, when one of the surfaces is maintained at a constant concentration given by the equilibrium solubility, and the other at zero concentration. Use the following data to derive the activation energy for diffusion:
| Temperature / K | Solubility /
|
Flux /
|
| 1250 | 13300 | 3.0 |
| 1140 | 20000 | 2.0 |
Calculate the activation energy for diffusion.
Explain why this is equivalent to the activation energy for the migration of the interstitial atom. Explain why when substitutional solutes diffusing by a vacancy mechanism do so at a much slower rate than interstitials?
What evidence is there that the diffusion of copper in nickel occurs by a vacancy mechanism.
The diffusion coefficients at the two temperatures are found using Fick's first law,
where 
is the foil thickness (0.25 mm), 
it the equilibrium solubility and the flux is stated in the table. Thus, the diffusivities at 1250 and 1140 K are found to be
and
respectively.
The activation energy is therefore 87.6
.
In general the activation energy is given by the sum of an energy of migration and that required to create a vacancy in the adjacent site. For interstitials there are plenty of vacancies so the activation energy for diffusion is identical to that for migration.
For substitutional solutes the diffusion activation energy must include both the migration energy and the energy of formation of a vacancy. Diffusion rates are therefore much slower.
The answer to the final part is the Kirkendall experiment. The student should describe the place exchange and ring mechanisms, neither of which lead to a net flux of atoms past the markers. Only vacancy diffusion leads to a motion of the couple relative to the markers when the two species have different intrinsic diffusion coefficients.
Explain the difference between mechanical twinning and annealing twins. How would you distinguish the two types of twinning using optical microscopy?
In cubic-close packed (c.c.p.) metals, the twin plane is 
and the twin direction is
. Calculate the twinning shear.
What is the maximum number of different twin traces that you might expect to find in any given grain of a severely deformed sample of a c.c.p. metal?
Explain why a shape memory metal (a) tends to lose its reversibility after many cycles; (b) why there is a limit to the amount of reversible strain in any given cycle. State two applications of shape memory metals.
Mechanical twinning is a deformation which involves the coordinated movement of atoms that leads to a reorientation of a part of the crystal. Annealing twins grow by a reconstructive mechanism from a deformed microstructure in much the same way as conventional grain growth. They do not lead to any deformation. Mechanical twins are lenticular in shape with sharp tips in order minimise strain energy. The shape of annealing twins is governed by the minimisation of interfacial energy. They are facetted on coherent interfaces with no sharp tips. Optical microscopy can also be used to study displacements at the free surface. Surface relief will only be observed with mechanical twinning. (5/20 + 1 bonus for surface relief).
Twinning involves a shift of each of the close packed planes by a distance
where 
is the lattice parameter. The spacing of the planes is 
. The twinning shear is the ratio of these two numbers, i.e. 
.
Four different traces (multiplicity of ) planes.
(a) The shape memory effect is not perfectly reversible in that a few defects are created on each cycle. This means that the defect density increases with the number of cycles, so much so that the interfaces are eventually prevented from reversible motion.
(b) When a shape memory element is deformed, the strain is accomplished by the growth of certain martensite orientations relative to others. Recoverable strain is exhausted when the element is converted entirely into one set of orientations. Any further deformation is ordinary plastic yielding and will damage the effect.
(c) Rings for joining, stents to keep arteries open, unbreakable spectacle frames 
Describe methods that you might use for the casting of the following items, justifying the equipment necessary and stating the reasons for the choice of the particular process:
(i) Some 3000 tonnes of molten steel which is subsequently to be rolled into plate. (ii) A propeller for a large ship. (iii) A ribbon of amorphous metal. (iv) A sample for the scientific study of homogeneous nucleation.
An aluminium-5 wt.% Cu alloy is unidirectionally solidified. Assuming no diffusion in the solid and complete mixing in the liquid phase, calculate the composition of the liquid at the point where solidification is 50% complete.
Why is it that the eutectic phase is sometimes observed in solidified ingots of Al-Cu even though the chemical composition and phase diagram indicate that the alloy should solidify before the eutectic temperature is reached?
(i) Continuous casting. The metal is poured into a tundish from which is flows into an oscillating water-cooled copper mould, leaving it with a solidified surface and a partly solidified core. The strand then bends around with the help of supporting rollers and is sliced into manageable chunks for hot-rolling operations. This is a much more efficient process than casting into molds in which pipe formation leads to considerable wastage.
(ii) This would be sand cast. It is a specialised item so that the sand mould can be custom made. The surface quality is not too important since the propeller can be machined subsequently.
(iii) Melt spinning since a high cooling rate is required. Involves directing a small jet of molten metal at a rapidly spinning water-cooled copper wheel.
(iv) Two methods: drop tube in which the sample is allowed to solidify whilst its is dropping and hence has no contact with an external surface. The second method involves solidification whilst the sample is levitating in a conical RF coil.
From the phase diagram (data book), the partitioning coefficient is given by
. We are given that 
and 
so using the Schiel equation we find that the composition of the solid at the interface is 
. It follows that the composition of the liquid is 
wt.% copper.
Nonequilibrium solidification causes an excessive solute concentration in the liquid, beyond that expected from the phase diagram, leading to eutectic phase.
What is the importance of the silicon concentration in the design of cast irons? How does the silicon concentration affect the hardness of cast iron?
There are two major variants of cast iron: white and grey. Carbon is mostly precipitated as graphite in grey iron whereas it occurs as cementite in white iron. Silicon retards the formation of cementite in which it has a negligible solubility. Its presence in a concentration of about 2 wt.% therefore encourages the formation of grey cast iron. Therefore, silicon reduces the hardness greatly by eliminating much of the cementite.
Explain how the shape memory effect associated with martensitic transformations works. Why is the memory diminished by repeated cycling? What sets the limit to the maximum recoverable strain?
Is it possible to have a shape memory polymeric material?
The shape deformation accompanying martensitic transformation can be reversed by transforming back to the parent phase. This, on its own, is NOT sufficient to explain how the shape memory effect works. Suppose a crystal of austenite is cooled to form many variants of martensite, in such a way that they accommodate; hence, the overall shape is unaffected by transformation (the first stage in Figure 1). When a stress is applied, the favoured variant of martensite grows, leading to a shape change which complies with the stress (the second stage. On heating the shape change is reversed, thus regaining the original shape. This is the basis of the shape memory effect.
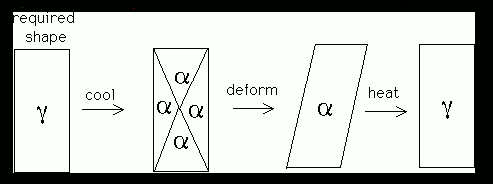
Figure 1: Shape memory effect
The memory effect relies on the reversibility of the shape deformation. It can be lost by the accumulation of defects during transformation, i.e. by repeated cycling.
Excessive deformation, beyond that required to produce a single martensite variant, will lead to irreversible plastic strain so that the original shape will become impossible to recover.
A once-only shape memory effect is possible with polymers. If the polymer chains are straightened during the fabrication of a component (shrink wrap) then heat will cause them to curl up again via the entropy spring effect.
Explain, in the context of binary solutions, what is meant by the term `chemical potential'. Hence justify the fact that the common tangent construction, on a free energy versus concentration plot, gives the equilibrium compositions of the phases.
Show how the diffusion coefficient can be written in terms of the chemical potential gradient rather than the concentration gradient. In what circumstances might the diffusion flux oppose the concentration gradient?
Consider an alloy consisting of two components 
and 
. For the phase 
, the free energy will in general be a function of the mole fractions 
and 
of and respectively:
represents the mean free energy of a mole of atoms in . The term 
is called the chemical potential of , and is illustrated in Figure 2a. Thus the free energy of a phase is simply the weighted mean of the free energies of its component atoms. Of course, the latter varies with concentration according to the slope of the tangent to the free energy curve, as shown in Figure 2.
Consider now the coexistence of two phases and 
in our binary alloy. They will only be in equilibrium with each other if the atoms in have the same free energy as the atoms in , and if the same is true for the atoms:
describes the mole fraction of element 
in phase which is in equilibrium with phase
The condition the chemical potential of each species of atom must be the same in all phases at equilibrium is quite general and obviously justifies the common tangent construction illustrated in Figure 2b.
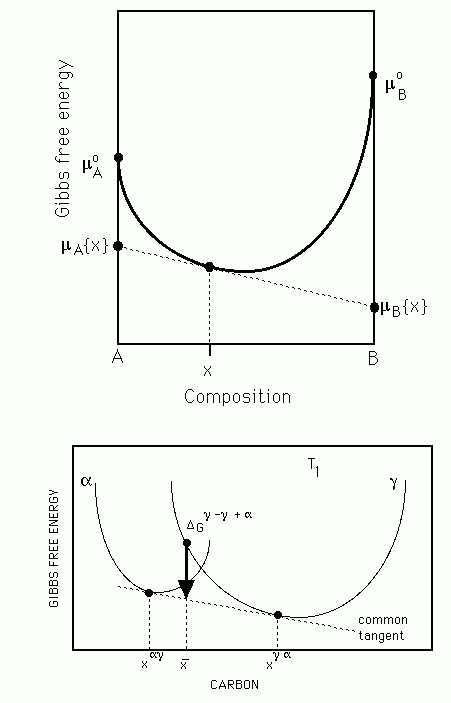
Figure 2 (a) Diagram illustrating the meaning of a chemical potential . (b) The common tangent construction giving the equilibrium compositions of the two phases at a fixed temperature.
Diffusion is driven by gradients of chemical potential ( i.e. free energy) rather than chemical concentration. By analogy with Fick's first law:
is known as the mobility of . In this equation, the diffusion coefficient is related to the mobility by comparison with Fick's first law.
The relationship is remarkable: if
then the diffusion coefficient is positive and the chemical potential gradient is along the same direction as the concentration gradient. However, if
then the diffusion will occur against a concentration gradient.
Distinguish between recovery, recrystallisation and grain growth.
Determine the limiting grain size during grain growth in a metal containing 1 volume percent of spherical inclusions whose average diameter is 600 nm. Explain any assumptions associated with your calculation.
What are the advantages and disadvantages of a fine-grained microstructure?
In recovery, there is a change in the stored energy without any obvious change in the optical microstructure. Excess vacancies and interstitials anneal out giving a drop in the electrical resistivity but little change in hardness. Dislocations become mobile at a higher temperature, eliminate and rearrange to give polygonisation. Still higher temperatures can lead to recrystallisation, during which new, relatively defect-free grains grow and consume the old deformed microstructure.
The recrystallised grain structure still contains a small amount of energy stored in the form of grain boundaries. The grains will tend to coarsen in order to reduce the amount of surface per unit volume. This is grain growth.
Equate the Zener drag pressure
to the grain growth pressure
to find the limiting grain size 
:
is the volume fraction of inclusion and 
is the particle radius. It follows that
.
The method assumes that the particles are all uniform in size, that all grain boundaries have identical energies per unit area, that the particles are randomly distributed.
Fine grains are desired for structural applications at low homologous temperatures, since they lead to an increase in strength via the Hall-Petch effect; grain size strengthening is the only way of improving toughness at the same time as strength. Of course, the surface per unit volume increases as the grain size decreases so a fine grain structure is not appropriate for elevated temperature applications where creep is an issue. Grain boundaries are easy diffusion paths.
Explain why the diffusion in a solid solution of interstitial solutes is so much more rapid than that of substitutional solutes. Vacancies are defects, so why does the vacancy concentration remain finite at equilibrium?
The activation enthalpy of diffusion can be separated into two components, one the enthalpy of migration (there are distortions of the lattice as the atom jumps into an adjacent potential well) and the enthalpy of formation of a vacancy in an adjacent site. After all, for the atom to jump it is necessary to have a vacant site. This latter component is unnecessary for interstitial atoms which consequently have a small activation enthalpy, and hence diffuse far more rapidly than do substitutional solutes.
The introduction of a vacancy increases the enthalpy, but the 
term due to configurations entropy reduces the free energy. These two opposing effects lead to an equilibrium concentration of vacancies at all but 0 K.
The surfaces of two samples of austenite is polished to a mirror finish. One of the samples is then heat treated to form a small amount of pearlite, and the other is cooled to form some martensite. Explain what you would expect to observe at the surface without etching the samples.
The formation of martensite would lead to large surface upheavals. In fact, each plate would cause an invariant-plane strain shape deformation which consists of a large shear (
) parallel to the habit plane, and a small dilatation (
) normal to the habit plane. Thus, the plates of martensite would be obvious without any etching.
Pearlite, by contrast, is not a displacive transformation and would leave the surface largely unaffected. The fact that the pearlite is present would not be seen without etching.
Explain how decarburisation causes a variation in the microstructure in a slowly cooled eutectoid steel as a function of the distance from the exposed surface.
A Fe-0.7C wt.% steel is decarburised at 1200 K such that a constant carbon concentration of 0.1 wt.% is maintained at the exposed surface. If the diffusion coefficient for carbon in austenite is
, how long will it take for the depth at which the concentration is 0.4 wt.% to become 2.5 mm?
How does your calculated time compare with an estimate made assuming that the diffusion distance is 
? Comment on why the two results are different.
How can decarburisation be prevented in practice?
By referring to the phase diagram, it can be deduced that the surface will be rich in ferrite, the unaffected regions away from the surface will be fully pearlitic. The intermediate regions will have a mixture of ferrite and pearlite according to the lever rule applied at the eutectoid temperature.
Using the error function solution given in the data book,
On the other hand, with
Decarburisation can be prevented by heat treatment in an intert atmosphere, by wrapping the component in stainless steel foil, or by painting with an isolating paint.
Silicon for the semiconductor industry has to be extremely pure. Describe the principles by which the purity can be increased duirng solidification processing.
The process is zone refining, where a molten zone is repeatedly traversed across a rod of silicon. The solubility of solute is generally larger in the liquid so it moves along with the zone, to be left at one end of the rod. That end can be cut off, the remainder being what is required.
Two phases are in equilibrium, one being richer in solute than the other. Explain why there is no diffusion even though the phases have different chemical compositions.
Diffusion is in general driven by a gradient of chemical potential, rather than a gradient of concentration. Phases are said to be in equilibrium when the chemical potential of each species is identical in both phases, i.e. the chemical potential is identical across the phase boundary. It follows that there is no driving force for diffusion.
What is the three-dimensional shape of martensite, a pearlite colony and of flake graphite in grey cast-iron? How can the shape of the flake graphite be modified into spheroidal graphite by alloying?
Martensite forms as thin plates (this minimises the elastic strain energy).
A pearlite colony is an interpenetrating bicrystal of ferrite and cementite. This can be visualised by thinking of a cabbage (single crystal cementite) in a bucket of water (single crystal ferrite).
Each flake of graphite is a part of a rosette of leaves. The addition of traces of rare earth elements such as Mg and Ce poisons fast growth directions, thus giving spheroidal graphite.
Suggest how a combination of deformation and heat treatment can be used to produce a fine grain structure in nickel. Why is a fine grain structure appropriate for low-temperature applications but not when the material is used at elevated temperatures?
Answer: Deformation increases the stored energy. This can be reduced by recrystallisation, in which `new" grains containing fewer defects are created. To obtain a fine grained microstructure, the sample is severely deformed so that the driving force for the nucleation of recrystallisation is large. The heat treatment should then be at a sufficiently high temperature to induce recrystallisation as opposed to recovery, but not so high that there is significant grain growth following the completion of recrystallisation.
A fine grain size increases the tensile strength by providing a greater number density or impediments to dislocation motion. It also increases toughness by reducing the number of dislocations that can be involved in a pile-up at a grain boundary. The stress concentration at the boundary is therefore reduced. It is therefore desirable to have a fine grain size when strength and toughness are important.
For elevated temperature applications, grain boundaries provide easy diffusion paths and therefore are to be avoided, since creep is often an issue for such applications.
