Part IB Metals and Alloys
Course A: Worked Examples (20-22)

H. K. D. H. Bhadeshia

Download postscript file
Download PDF file

Question 20

Describe an experiment which can prove that diffusion occurs by a vacancy mechanism rather than a mechanism in which adjacent atoms simply swap positions.

Stating assumptions, derive an equation to show how the measured diffusion coefficient depends on the grain size of a polycrystalline material.

What role do grain boundaries play in the performance of turbine blades used in the construction of aeroengines, and how may you minimise their deterimental effects?

Answer 20

The Kirkendall experiment. Describe the place exchange and ring mechanisms, neither of which lead to a net flux of atoms past the markers. Only vacancy diffusion leads to a motion of the couple relative to the markers when the two species have different intrinsic diffusion coefficients.

For a unit area, the overall flux is the sum of that through the lattice and that through the boundary:

$\begin{displaymath} J \simeq J_P + J_{gb}{{2\delta}\over{d}} \end{displaymath}$

$\begin{displaymath}\hbox{so that}\qquad D_{measured} = D_P + D_{gb}{{2\delta}\over{d}} \end{displaymath}$

where $\delta$ is the thickness of the grain boundary.

Grain boundaries provide paths for easy diffusion and hence increase the rate of creep. The blades were at first polycrystalline, later to be replaced by directionally solidified blades so that the creep rate along the axis is reduced, and finally by single crystal turbine blades.

Question 21

What is the importance of the silicon concentration in the design of cast irons? How does the silicon concentration affect the hardness of cast iron?

Stating reasons, describe metallic alloys and casting process which would be suitable for making the following cast components:

An engine block for a modern car.
A toy car.
A turbine blade containing internal cooling-channels.

Answer 21

There are two major variants of cast iron: white and grey. Carbon is mostly precipitated as graphite in grey iron whereas it occurs as cementite in white iron. Silicon retards the formation of cementite in which it has a negligible solubility. Its presence in a concentration of about 2 wt.% therefore encourages the formation of grey cast iron. Therefore, silicon reduces the hardness greatly by eliminating much of the cementite. Naturally, white cast irons are much harder because the carbon is present as cementite.

An engine block would be made out of an aluminium-12 wt% silicon eutectic composition because this gives the minimum melting temperature. The silicon which has a density of just 2.34 $\,{\rm g\,cm^{-3}}$ , precipitates virtually as pure silicon. The resulting expansion compensates for freezing contractions to give castings with minimal porosity. The silicon is coarse and brittle. The addition of a minute quantity of sodium (0.02 wt%) greatly refines the Si particles giving a higher toughness.

The toy would be made by die-casting which involves the injection of a low-melting temperature alloy into a steel mould. Zn-4Al wt%, which is a eutectic composition, is a classic die-casting alloy melting at 419^oC. The process is usually for non-structural components since the casting inevitably contains internal pores and because Zn does not have particularly good mechanical properties. However, productivity can be high and the surface finish is good.

A heat-resistant nickel base alloy cast using the lost wax process in which a wax model is surrounded by ceramic, the wax is then burnt off and the metal cast into the ceramic mould which is finally broken away to reveal the precise and beautiful casting.

Question 22

The isothermal data below represent measurements of the thickness of a precipitate as a function of time as it grows by solid-state transformation. What is the process which controls the growth of the precipitate? Determine the solute diffusion coefficient given that $\Delta C_{ss}/\Delta C_{\alpha\beta} = 0.2$ .

Thickness / m $\times 10^{-6}$ 1 2 3 4 5 6 7 8
Time / s 1 4 9 16 25 36 49 64

Explain why does growth rate decreases as the particle becomes thicker.

Answer 22

The thickness varies with the square root of time (Fig. a), meaning that the process is diffusion-controlled.

From data book, the velocity is given by

$\begin{displaymath}v \simeq {{\Delta C_{ss}}\over {\Delta C_{\alpha\beta}}} \sqrt{{{D}\over{t}}}\end{displaymath}$

so that the thickness is given by

$\begin{displaymath}x\simeq 2{{\Delta C_{ss}}\over {\Delta C_{\alpha\beta}}} \sqrt{Dt}\end{displaymath}$

From this it follows that $D = 6.25\times 10^{-12}\,{\rm m^2\,s^{-1}}$ .

The growth rate decreases with time (Figure). The physical reason why the growth rate decreases with time is apparent from mass balance. As the precipitate grows, the total amount of solute absorbed must equal that depleted from the matrix. Thus, the diffusion distance $\Delta x$ is proportional to the precipitate size (Figure). As a consequence, the concentration gradient decreases as the precipitate thickens, causing a reduction in the growth rate.

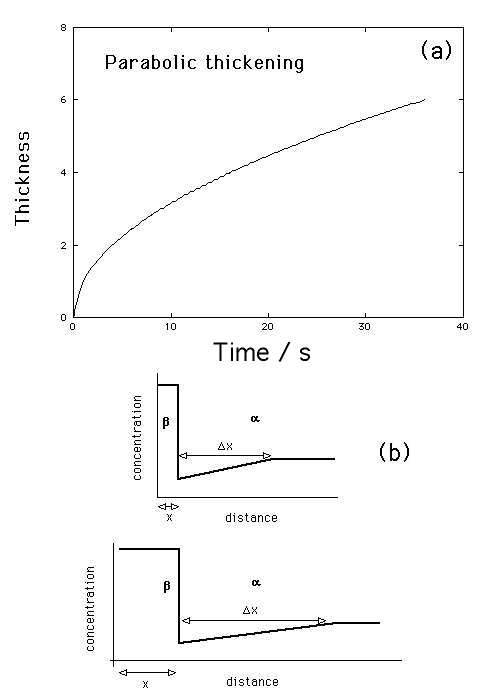
(a) Parabolic thickening during one dimensional growth. (b) Increase in diffusion distance as the precipitate thickens.

H.K.D.H. Bhadeshia
2001-06-30

Part IB Metals and Alloys Course A: Worked Examples (20-22)