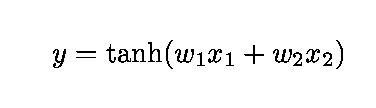

The hyperbolic tangent is a common transfer function in neural networks. One reason is that it is a very flexible, non-linear function. It is also continuous and differentiable. The intention here is to illustrate its flexibility.
This example illustrates the flexibility of a hyperbolic tangent in which the output y is expressed as a function of two inputs x1 and x2 . The shape of the surface changes as the weights w1 and w2 are varied. The equation below is the actual function being plotted.
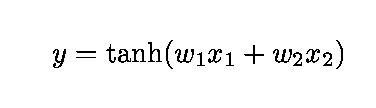
This example illustrates how combining a variety of hyperbolic tangents gives even greater flexibility. There output y is expressed as a function of two inputs x1 and x2. The shape of the surface changes dramatically as the weights w1 and w2 are varied in the range 0-10. The equation below is the actual function being plotted.
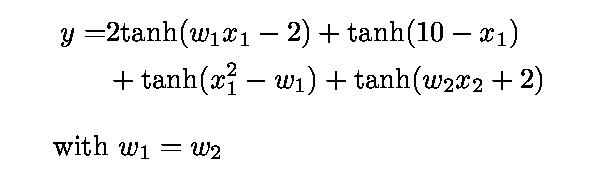
A neural network with four hyperbolic tangents would be said to have four hidden units.
Click to start another simulation
| PT Group Home | Materials Algorithms |