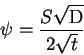 |
(1) |
Precipitation phenomena in creep-resistant austenitic stainless steels are numerous and complex, with a large number of possible phases forming during long term exposure to high temperature [1]. The occurrence of these different precipitates are interdependent and sensitive to small composition changes [1,2]. Any attempt to model the decomposition of austenite into several phases should therefore take into account the competition for solute and nucleation sites and space. Recent works by Robson and Bhadeshia [3], or Fujita and Bhadeshia [4] have demonstrated the possibility to model interaction between various precipitation reactions in steels. This work is concerned with the development and improvement of a similar model for austenitic stainless steels.
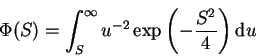 |
(3) |
 |
For small supersaturations (
![]() ) this can be
approximated by
) this can be
approximated by
![]() while for large
supersaturations (
while for large
supersaturations (
![]() ),
),
![]() ; further details can be found in
[6].
; further details can be found in
[6].
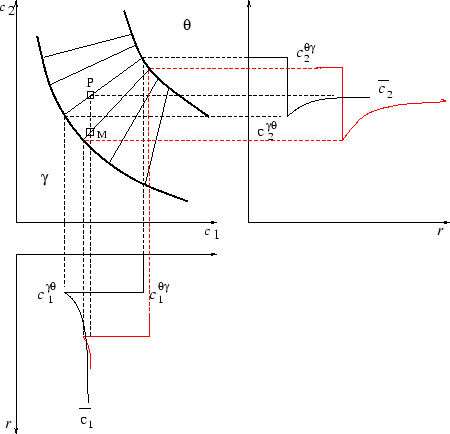
When two solutes have significantly different diffusivities, the
particular tie-line which allows the set of equations
4 to be satisfied, i.e. the flux-balance
tie-line, will in general be different from that passing through
![]() , as illustrated in figure 2 for a
ternary system.
, as illustrated in figure 2 for a
ternary system.
 |
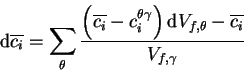 |
(7) |
In the classical Avrami theory, or in its adaptation to simultaneous reactions [3], the increase in volume fraction is corrected to account for the presence of transformed regions. This correction was neglected throughout, a reasonable approximation given the small volume fractions involved.
|
Data were less readily available for Nb, Ti and Mo for these steels, and these coefficients, when required in calculations were set to be equal to that of chromium. Similarly, in all cases, the activation energy for transfer across the nucleus interface Gt* was taken to be about the activation energy for chromium diffusion, 250 kJ.mol-1.
For the case of , the following approximations were made when
evaluating the local equilibrium at the transformation front.
Because the diffusion coefficient of carbon is larger than that of the
substitutional elements, it was assumed that carbon achieves a uniform
activity instantaneously.
Once the tie-line consistent with carbon isoactivity was identified,
the interface velocity was calculated on the basis of the
corresponding chromium flux:
| (8) |
 |
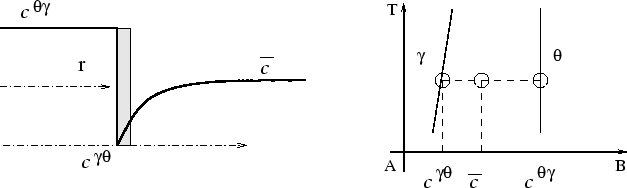
As illustrated in figure 3, the calculated growth rate of compares well with data obtained by Záhumenský [12] for a type 316 steel at 650 . Alternative models have used the Cr gradient as defined by the mass-balance tie-line [3,16], labelled Cr-control in figure 3, or the zero carbon-gradient tie-line [4], labelled Cr-C control in figure 3. These methods have been shown to under or over estimate the actual growth rate respectively.
Further validation for this method is obtained when comparing measured and predicted Cr/Fe ratios in : it has frequently been reported [17,15,18] that the ratio Cr/Fe is significantly lower at the early stages of precipitation than it is at equilibrium, and gradually increases with ageing time. Such behaviour is correctly predicted by the model (figure 3). Table 2 compares the predicted initial composition of in AISI 304 to the measured values given by Boeuf [17].
|
 |
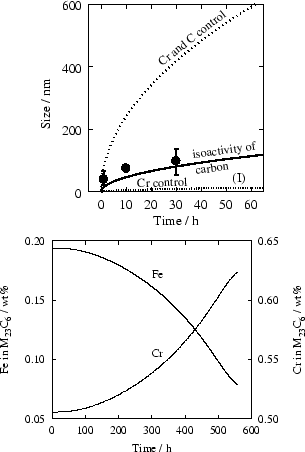
It should be noted that the behaviour and final amount of phases are dictated by the underlying thermodynamic models. In this case, TiC is predicted to be the stable phase. Discrepancies have been reported [1] on the behaviour of Ti stabilised steels.
In general, there is little quantitative information regarding precipitation in austenitic stainless steels. Furthermore, results obtained by different methods differ significantly. For example, the work utilised in the previous section, from Thorvaldsson and Dunlop [19], indicates that the maximum volume fraction of MC type carbides (mainly TiC) is reached after about 1000 h, on the basis of TEM investigations. On the other hand, Thorvaldsson [15], in a different publication on a similar steel, for identical conditions, report the maximum volume fraction of MC type carbides (mixed (Ti,Nb)C) to be reached after 3 to 8 hours, on the basis of resistance measurements. There is no comments from the authors as to the largely different kinetics of precipitation.
This makes it difficult to estimate the adjustable parameters N and
![]() for these phases. However, the time scale for
the formation of such carbides and nitrides remains small in
comparison with the typical lifetime in creep, and therefore the error
introduced in the precipitation sequence is of little consequence.
for these phases. However, the time scale for
the formation of such carbides and nitrides remains small in
comparison with the typical lifetime in creep, and therefore the error
introduced in the precipitation sequence is of little consequence.
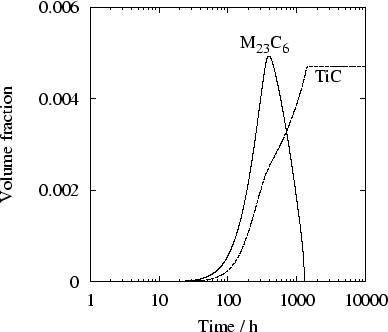
With
![]() m-3 and
m-3 and
![]() J/m2, satisfying agreement was
obtained between the predictions and both the
time-temperature-precipitation diagram and the quantitative
measurements provided by these authors (figures 5 and
6).
J/m2, satisfying agreement was
obtained between the predictions and both the
time-temperature-precipitation diagram and the quantitative
measurements provided by these authors (figures 5 and
6).
 |
The disagreement at high temperatures is essentially due to
thermodynamic data on which the calculations rely: the NPL PLUS
database (based on SGTE SSOL) predicts an equilibrium amount
of ![]() -phase (1.7%) which is not consistent with the
observations made by Minami [20].
-phase (1.7%) which is not consistent with the
observations made by Minami [20].
Furthermore, this fitting can only be semi-quantitative, as there
remains the problem of the detection limit, which may not scale with
the volume fraction: at high temperature, few precipitates of large
size are expected, while at low temperature, one expects smaller but
more numerous precipitates. This means that, unless an exact
determination of the volume fraction is carried out, ![]() -phase
might be detected at lower volume fraction at high temperatures.
-phase
might be detected at lower volume fraction at high temperatures.
Figure 6 shows the evolution of the volume
fraction of ![]() -phase as a function of ageing time at 700
, in different steels of the AISI 300
series.
-phase as a function of ageing time at 700
, in different steels of the AISI 300
series.
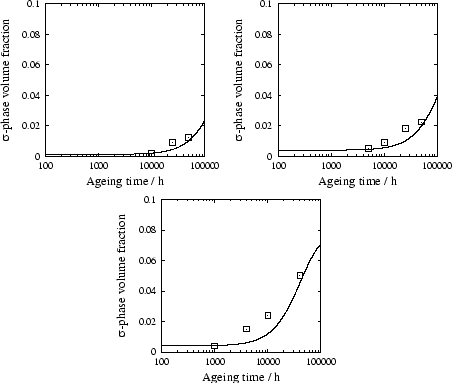 |
Initially, the nucleation parameters obtained for AISI 304 were used
to predict the formation of ![]() -phase in 316 (304 with Mo) and 347
(Nb-stabilised). The results were opposite to the observed
trends, with the formation of
-phase in 316 (304 with Mo) and 347
(Nb-stabilised). The results were opposite to the observed
trends, with the formation of ![]() predicted to be slowest in
347, where it is observed to be the fastest. This problem is directly
related to the predicted driving forces in the different steels, shown
in table 3.
predicted to be slowest in
347, where it is observed to be the fastest. This problem is directly
related to the predicted driving forces in the different steels, shown
in table 3.
However, examination of the different micrographies published in [20] revealed considerable difference in grain sizes between 304 and 347. The mean linear intercept was estimated to be 3.7 times smaller in the latter steel. The nucleation site density was therefore corrected so as to account for the smaller grain size: the model essentially considers grain boundary nucleation, implying that the number density should be 3.72 greater in 347 than in 304. Once this correction made, better agreement is obtained as 347 is correctly predicted to occur faster in 347 than in 304, despite the lower driving force. Calculations with the corrected nucleation parameters are shown in figure 6.
The predicted increase is generally slightly steeper than that measured. It was verified however, that saturation of the nucleation sites was reached in the very early stages of the precipitation, which corresponds to the least steep curve for a given growth rate. The explanation for the discrepancy was therefore expected to be found in the simple growth model adopted.
It must be emphasised at this point that very few of the parameters in this model are user-selected; for example, diffusion coefficients, interface compositions and driving forces are indirectly provided by thermodynamic databases, there is therefore little lattitude to modify the calculated growth rate for a given phase using the `natural' parameters such as diffusion coefficient, supersaturation etc.
By artificially multiplying the interface velocity for ![]() -phase
by a factor varying between 0.2 and 1.5, the effect on the
steepness of the growth curves could be investigated. It was found
that, once the nucleation site density modified to obtain curves
located at the same times, the gradient of the volume fraction vs time curves was not significantly changed.
Furthermore, the final particle sizes obtained for
-phase
by a factor varying between 0.2 and 1.5, the effect on the
steepness of the growth curves could be investigated. It was found
that, once the nucleation site density modified to obtain curves
located at the same times, the gradient of the volume fraction vs time curves was not significantly changed.
Furthermore, the final particle sizes obtained for ![]() -phase were
in best agreement with typical sizes observed in [20] when
the growth rate was left unchanged, with predicted sizes of 3.8
-phase were
in best agreement with typical sizes observed in [20] when
the growth rate was left unchanged, with predicted sizes of 3.8 ![]() m
after 50000 h at 700 , compared to an observed size of 4.2
m
after 50000 h at 700 , compared to an observed size of 4.2
![]() m in the AISI 347 studied in [20]. It is therefore
concluded that the difference is not the result of the simple growth
model adopted, but is most likely the result of the mean-field
approximation, as only an enhanced soft-impingement could further
decrease the steepness of the volume fraction vs time
curves. Further work is required in order to improve on this approximation.
m in the AISI 347 studied in [20]. It is therefore
concluded that the difference is not the result of the simple growth
model adopted, but is most likely the result of the mean-field
approximation, as only an enhanced soft-impingement could further
decrease the steepness of the volume fraction vs time
curves. Further work is required in order to improve on this approximation.
Barcik [21] proposed that ![]() phase formation is
most strongly affected by grain size, that is, by nucleation site
density. Minami [20] have opposed this viewpoint,
and proposed that the driving force is a predominant factor in the
rate of
phase formation is
most strongly affected by grain size, that is, by nucleation site
density. Minami [20] have opposed this viewpoint,
and proposed that the driving force is a predominant factor in the
rate of ![]() -phase formation. However, the present study, on the
basis of their own data, indicates that, although the driving force
might have an effect, it is expected to be of small influence compared
to the grain size, or any other parameter which could result in an
increase in nucleation site density. In fact, use of the driving force
alone leads to predictions of trends opposite to the observed
ones.
-phase formation. However, the present study, on the
basis of their own data, indicates that, although the driving force
might have an effect, it is expected to be of small influence compared
to the grain size, or any other parameter which could result in an
increase in nucleation site density. In fact, use of the driving force
alone leads to predictions of trends opposite to the observed
ones.
Calculations indicate, in general, that ![]() -phase is considerably
more difficult to nucleate than most carbide phases, and therefore
confined to relatively high-energy defects. This suggests that the
method recently used to control sensitisation [22], by which
the average grain boundary energy is reduced by a carefully designed
thermo-mechanical treatment, may also lead to suppression, or
significant delay, of
-phase is considerably
more difficult to nucleate than most carbide phases, and therefore
confined to relatively high-energy defects. This suggests that the
method recently used to control sensitisation [22], by which
the average grain boundary energy is reduced by a carefully designed
thermo-mechanical treatment, may also lead to suppression, or
significant delay, of ![]() -phase formation.
-phase formation.
The validity of these conclusions is obviously dependent on that
of the predicted driving forces, that is, ultimately, on the
thermodynamic database used in this study (NPL plus, based on SGTE
SSOL), and on the hypothesis that the interfacial energy
![]() does not vary significantly between the three
grades. This seems a reasonable assumption given their similar
compositions.
does not vary significantly between the three
grades. This seems a reasonable assumption given their similar
compositions.
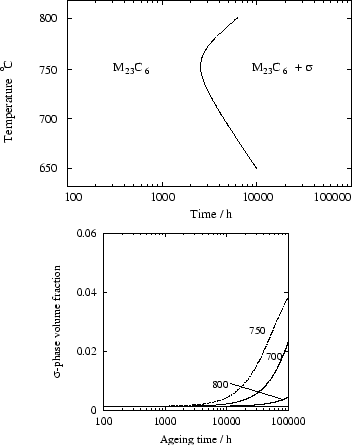
Figure 7 shows the complete precipitation
sequence for an AISI 316 steel, at 700 , which is in good
agreement with the work of Minami [20]. However, at
750 , ![]() phase is found experimentally, but is not
predicted to form by the model. This is because, according to MT-DATA,
the driving force for its formation is zero throughout the
precipitation sequence.
phase is found experimentally, but is not
predicted to form by the model. This is because, according to MT-DATA,
the driving force for its formation is zero throughout the
precipitation sequence.
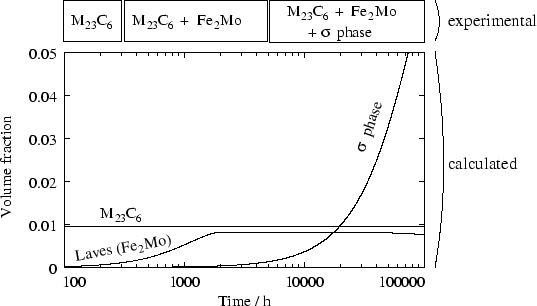 |
It is important to note that a simple equilibrium calculation will not
predict the presence of Laves phase (Fe2Mo), which only exists as
a transient phase, and dissolves as ![]() -phase precipitation
progresses. Although there is no driving force for the formation of
Laves phase once
-phase precipitation
progresses. Although there is no driving force for the formation of
Laves phase once ![]() -phase is formed, this is not the case if the
supersaturated matrix composition is considered. In a similar way,
there is a driving force for precipitation of from the
initial supersaturated matrix, in the example illustrated in figure
4, however TiC is ultimately the only
stable carbide.
-phase is formed, this is not the case if the
supersaturated matrix composition is considered. In a similar way,
there is a driving force for precipitation of from the
initial supersaturated matrix, in the example illustrated in figure
4, however TiC is ultimately the only
stable carbide.
A physically-based model to predict precipitation sequences has been presented that accounts for interactions between the different kind of phases forming in austenitic stainless steels. The underlying growth model was shown to give satisfying quantitative agreement when required thermodynamic data were available. The overall kinetics are in satisfying agreement with the published observations, particularly in regard of the relative simplicity of the model. However, this success is necessarily limited to phases for which thermodynamic data are available.
This is unfortunately not the case for a number of phases observed in austenitic stainless steels: in Nb rich steels (AISI 347) in which Fe2Nb and Fe3Nb3C are expected to form when Nb is in excess [1]. Although the formation of the former is correctly predicted, its dissolution for the latter cannot be accounted for, since there are no thermodynamic data for Fe3Nb3C. Phases such as X or Z-phase are not represented in the SGTE database, therefore making difficult any meaningful prediction on nitrogen bearing steels.
It was shown that the composition change of can be correctly
predicted which suggests it could be used as an indicator of the
progress of the precipitation. The present model also supports the
suggestion that ![]() -phase formation depends above all on the
number of high-energy nucleation sites, the driving force being of
lesser importance.
-phase formation depends above all on the
number of high-energy nucleation sites, the driving force being of
lesser importance.
The code for the corresponding software is freely available on https://www.msm.cam. ac.uk/map/, together with the data used for the predictions shown in the present publication.
This document was generated using the LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 -title 'Multiple precipitation reactions in austenitic stainless steels' -white -noparbox_images -math_parsing -notop_navigation -nonavigation -dir ./ MAIN.tex
The translation was initiated by on 2003-08-04