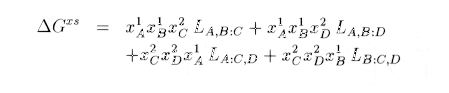PURE SUBSTANCE: simply defined by its free energy of formation and coefficients for the expression of the heat capacity Cp. Its free energy is therefore only dependent on T and P.
REDLICH-KISTER: This model express the excess free energy of mixing as the sum of terms which consist of a function of the mole fractions of each component and a interaction parameter. If only one parameter is non zero the expression becomes the one for a regular solution, if two are present, we have a sub-regular solution. The Redlich-Kister expansion can be written:
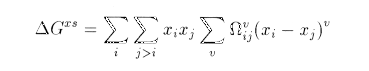
SUBLATTICE: If we consider in a general way the mixing of n components Ai of mole fraction xi , the entropy of mixing is given by the sum of xi ln (xi) . This assumes that all the components can take whatever position they want in the mix.
However, in practice, it is often the case that two kinds of elements
are on different sublattices, as carbon is only in the intersticial sites
in austenite for example.
To handle this, different sublattices are defined (two in the case
of austenite) on which elements can mix.
With the system we defined, Fe and Cr will mix on a first sublattice
while C and Vacancies (Va) will mix on a second one. The interactions between
the different components are now modeled using parameters of the kind:
L(A,B:C)
where a column represents the separation between two sublattices, and the coma between two components. This is then the parameter for interaction between A and B on the first sublattice when C is on the second one. The expression for a sublattice model can be: