Part II : Worked Examples (5-13)

H. K. D. H. Bhadeshia

Download Postscript file
Download PDF file

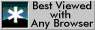
Worked Examples 1-4
Worked Examples 14-20
Worked Examples 21-29
Worked Examples 30-33

Question 5

Using the concept of forces and fluxes in the theory of irreversible thermodynamics, deduce the relationship between the velocity $V$ of a grain boundary and the free energy change $\Delta G$ accompanying it motion. State any assumptions involved in this derivation.

Prove that the general relation between $V$ and $\Delta G$ should in fact be as follows:

\begin{displaymath}V \propto \exp\{-Q/kT\}[1-\exp\{-\Delta G/kT\}] \end{displaymath}

where $Q$ is the activation energy for the transfer of atoms across the grain boundary, $k$ is the Boltzmann constant and $T$ is the absolute temperature.

Is it possible to reconcile this equation with the relationship deduced from irreversible thermodynamics?

Answer 5

In an irreversible process, the product of the force $Z$ and the flux $J$ gives the rate of energy dissipation:

\begin{displaymath}T\sigma = JZ\end{displaymath}

where $T$ is the temperature, $\sigma$ is the rate of entropy production. $T\sigma$ is therefore the rate of energy dissipation. In many cases, it is found experimentally that $J\propto Z$.

In the case of grain boundary motion, the rate of energy dissipation is simply $V\Delta G$ so that we immediately get

\begin{displaymath}V \propto \Delta G\end{displaymath}

An alternative is to consider the transfer of atoms across a grain boundary (a barrier of height $Q$). The probability of forward jumps (jumps which lead to a reduction in free energy) is given by

\begin{displaymath}\exp\{-Q/kT\}\end{displaymath}

whereas that of reverse jumps is given by

\begin{displaymath}\exp\{-(Q+\Delta G)/kT\}= \exp\{-Q/kT\}\exp\{-\Delta G/kT\}\end{displaymath}

.

The rate at which an interface moves is therefore given by

\begin{displaymath}V \propto \exp\{-Q/kT\}[1-\exp\{-\Delta G/kT\}] \end{displaymath}

Note that this relation is hardly that predicted from irreversible thermodynamics. However, they become identical when $\Delta G$ is small, there is not a great deviation form equilibrium. Note that for small $x$, $\exp\{x\} \simeq 1+x$. Thus, at small driving forces,

\begin{displaymath}V_i \propto \exp\{-Q/kT\}[\Delta G/kT]\end{displaymath}

Question 6

In what circumstances does the diffusion coefficient of a solute become zero?

Answer 6

In solutions where clustering is favoured where the solution has a free energy curve of the form illustrated below. At the points of inflexion, the diffusion coefficient is zero, whereas in-between it is negative (spinodal decomposition, uphill diffusion).

Free energy curve of a solution where the enthalpy of mixing is positive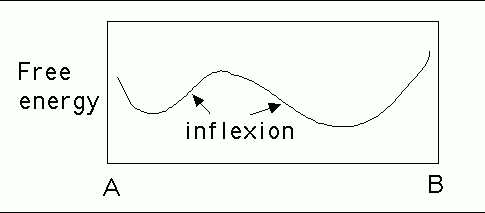



Question 7

Why does ferritic iron change from a ferromagnetic to paramagnetic state as the temperature is raised?

Answer 7

Ferromagnetism involves the alignment of unspinpaired electrons. This is favoured by the accompanying reduction in enthalpy, but there is also an increase in free energy due to a reduction in entropy. As the temperature increases, the free energy increase caused by the reduced entropy of ordering dominates, because it scales with $T$. Hence, magnetic ordering is destroyed, giving paramagnetic iron.



Question 8

Prove that the distance $R$ between the transmitted beam, and the diffracted beam, as measured on an electron diffraction pattern obtained using a transmission electron microscope is proportional to the reciprocal of the spacing $d$ of planes giving rise to the diffracted beam.

How would you expect $R$ to change if the operating voltage of the electron microscope is increased?

How would you find the Miller indices of the long axis of a rod-shaped crystal, given a bright field image and an electron diffraction pattern taken without moving the crystal?

Answer 8

The diffraction geometry is illustrated below. Since the Bragg angle $\theta$ is small, it follows that:

\begin{displaymath}\tan (2\theta) \simeq 2\theta = R/L\end{displaymath}

From the Bragg equation,

\begin{displaymath}2\sin (\theta) \simeq 2\theta = \lambda/d \end{displaymath}

so that

\begin{displaymath}{{R}\over{L}} = {{\lambda}\over{d}} \end{displaymath}

The wavelength $\lambda$ decreases as the accelerating voltage increases. Hence, $R$ would decrease.

Electrons follow a spiral path through the column, because electrons spiral in a magnetic field. The pitch of the spiral changes with the strength of the lenses. The lenses are adjusted to project the image plane on to the screen when imaging, and the back focal plane when recording the diffraction pattern. Consequently, the pitch of the spiral is different in the two cases, so that the diffraction pattern is rotated relative to the image. Hence, to obtain the rod-axis it is necessary to correctly orient the diffraction pattern to the image.



Question 9

How would you measure the spacing and perfection of a multilayered composite consisting of alternating layers of gold an silver, each of thickness a few nanometres?

Answer 9

The layered structure introduces an additional periodicity (above that of the crystal structure), so that satellite reflections appear in the electron diffraction pattern. Therefore, the spacing can be determined directly. The number of satellite reflections along a row is a measure of the perfection of the layered structure.



Question 10

Explain how a scanning tunnelling microscope works.

Answer 10

A sharp needle approaches a surface, until electron tunnelling gives rise to a tunnelling current between the needle and the sample. This current is a signal, so that the needle position relative to the sample surface can be monitored.

The signal is used to maintain the needle at a constant distance, and hence it is possible to plot out the surface contours on an atomic scale (since the tunnelling distance is of that order). The needle height can be controlled on an atomic scale by using the signal to stimulate a piezoelectric crystal.



Question 11

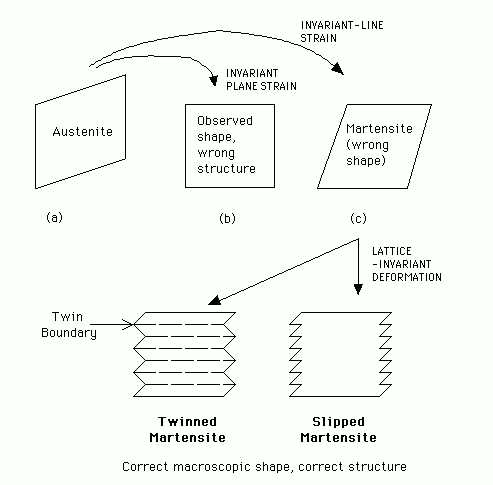
How would you prove that martensitic transformation is diffusionless?

In steels, the strain needed to change the structure of austenite into that of martensite is an invariant-line strain. However, the shape deformation observed when martensite grows is an invariant-plane strain. Show schematically how these different deformations may be reconciled, and hence explain why martensite frequently contains transformation twins.

Explain the role of the alloying elements in the following high-strength steel which has a quenched and tempered martensitic microstructure:

Fe-2.0Mn-0.4C wt.%

State a typical heat-treatment for this alloy, and explain how the steel may be improved to achieve even higher strength without sacrificing toughness.

Answer 11

Martensite is diffusionless because: (a) Its composition is identical to that of austenite, a necessary but not sufficient condition; (b) it can grow at 1100 ${\rm m\,s^{-1}}$, a growth velocity which is far in excess of any diffusion velocity; (c) it can grow at temperatures as low as 4 K where diffusion is inconceivable within the time frame of the experiment.

The strain illustrated in going from (a) to (c) leaves the line normal to the diagram unchanged (an invariant-line strain). However, the observed change of shape is an invariant-plane strain illustrated in the change from (a) to (b), the invariant plane being the vertical side of (a). The structure of (b) is therefore wrong, but its shape correct. The shape of (c) is wrong but its structure correct.

This can be resolved by adding a further deformation which does not change the structure (slip or twinning), but which gives the correct macroscopic shape corresponding to (b).

The manganese is for hardenability, the carbon for strength. Typical heat-treatment - austenitise at 1123 K for an hour, quench in oil, temper at about 673 K for 1 hour. The low austenitisation temperature avoids austenite grain coarsening. The high tempering temperature avoids a toughness minimum at about 623 K, caused by coarse cementite. Add about 1 wt.% of silicon to the steel to retard precipitation of cementite, so that the toughness dip is moved to higher tempering temperatures. Thus, the modified steel can be tempered at only 573 K for 1 hour to retain a higher level of strength.



Question 12

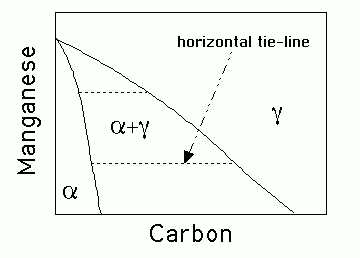
Explain what is meant by the term paraequilibrium. Illustrate schematically an isothermal section of the paraequilibrium phase diagram for an Fe-Mn-C alloy where austenite and ferrite can coexist. The sketch should include tie-lines.

Answer 12

Paraequilbrium is a constrained equilibrium. It occurs at temperatures where the diffusion of substitutional solutes is not possible within the time scale of the experiment. Nevertheless, intersitials may remain highly mobile. Thus, in a steel, manganese does not partition between the ferrite and austenite, but subject to that constraint, the carbon redistributes until it has the same chemical potential in both phases.

Therefore, the tie-lines in the phase diagram are all virtually parallel to the carbon axis, since Mn does not partition between ferrite and austenite.



Question 13

The Avrami equation give the fraction $\xi$ of transformation as

\begin{displaymath}\xi = 1 - \exp\{-\pi G^3It^4/3\}\end{displaymath}

when the product grows in the for of spheres at a constant rate $G$, with a constant nucleation rate $I$ per unit volume during a time interval $t$. How would the exponent of time change if (a) growth is diffusion-controlled; (b) growth begins instantaneously from all of a fixed number of nucleation sites.

Answer 13

The Avrami equation come from the integration of

\begin{displaymath}-\ln(1-\xi) = (4\pi/3)\int^t_0G^3I(t-\tau)^3d\tau\end{displaymath}

where $\tau$ is the incubation period for each particle.

When the dimension of the particle does not change as $G(t-\tau)$ but instead varies with $t^{1/2}$ ( diffusion-controlled growth), the time exponent in the final equation will be reduced to $5/2$. This is because the volume of each particle scales with $t^{3/2}$ and an additional $t$ comes from the nucleation rate.

When there is no nucleation but growth starts instantaneously from a fixed number of sites, the time exponent is obviously reduced to 3.

Worked Examples 1-4
Worked Examples 14-20
Worked Examples 21-29

H.K.D.H. Bhadeshia
2000-06-09