Part II Metals and Alloys:Worked Examples (21-29)

H. K. D. H. Bhadeshia

Download Postscript file
Download PDF file

Worked Examples 1-4
Worked Examples 5-13
Worked Examples 14-20
Worked Examples 30-33

Question 21

In an Fe-C alloy, the isothermal growth of ferrite occurs with equilibrium maintained locally at the interface such that

\begin{displaymath}(c^{\alpha \gamma} - c^{\gamma \alpha})v = D{{\partial c}\over{ \partial z}}\end{displaymath}

where $c^{\alpha \gamma}$ is the concentration of carbon in ferrite which is in equilibrium with austenite, $c^{\gamma \alpha}$ is the corresponding concentration in austenite which is in equilibrium with ferrite, $D$ is the diffusivity of carbon in austenite, $v$ is the interface velocity and $z$ is a coordinate defined normal to the interface. The concentration gradient is evaluated at the position of the interface.

Explain separately the meanings of the left and right hand sides of this equation, and hence the origin of the equation.

How would similar conditions be derived for a ternary Fe-Mn-C alloy?

Hence describe two ways in which ferrite can grow in a ternary Fe-Mn-C alloy whilst maintaining local equilibrium at the interface, even though the diffusivities of Mn and C are different by many orders of magnitude.

Explain what is meant by the term paraequilibrium. Illustrate schematically an isothermal section of the paraequilibrium phase diagram for an Fe-Mn-C alloy where austenite and ferrite can coexist. The sketch should include a few tie-lines.

Answer 21

The boundary condition defined by the equation relates the interface velocity to the concentration gradient at the interface. The rate at which solute is partitioned as the interface moves ( i.e. left hand side) must equal that at which it is carried away by diffusion ( i.e. right hand side) if the compositions at the moving interface are to remain constant.

For a ternary alloy it would be necessary to satisfy two such equations simultaneously, for each of the solutes:

\begin{displaymath}\left.\eqalign{ (c_1^{\gamma \alpha} - c_1^{\alpha \gamma})v... ...\alpha} - c_2^{\alpha \gamma})v &= -D_{2} \nabla c_2}\right\} \end{displaymath}

where the subscripts refer to the solutes (1 for carbon and 2 for Mn).

Because $D_{1}\gg D_{2},$ these equations cannot in general be simultaneously satisfied for the tie-line passing through the alloy composition $\overline{c}_1,\overline{c}_2.$ It is, however, possible to choose other tie-lines which satisfy equation . If the tie-line is such that $c_1^{\gamma \alpha}=\overline{c}_1$ (line cd for alloy A of Figure 1a), then $\nabla c_1$ will become very small, the driving force for carbon diffusion in effect being reduced, so that the flux of carbon atoms is forced to slow down to a rate consistent with the diffusion of manganese. Ferrite forming by this mechanism is said to grow by a ` Partitioning, Local Equilibrium' (or PLE) mechanism, in recognition of the fact that $c_2^{\alpha \gamma}$ can differ significantly from $\overline{c}_2$, giving considerable partitioning and long-range diffusion of manganese into the austenite (Coates, 1973c).



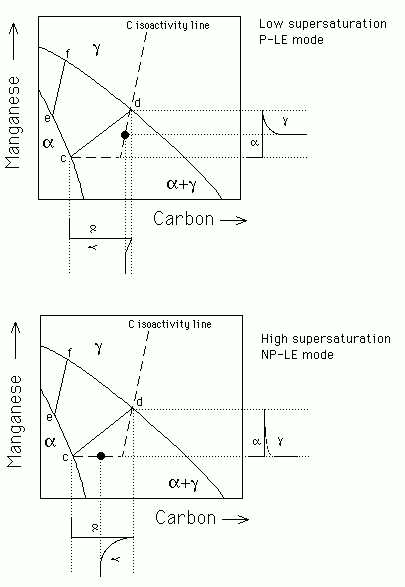
Figure 1: Schematic isothermal sections of the Fe-Mn-C system, illustrating ferrite growth occurring with local equilibrium at the $\alpha / \gamma $ interface. (a) Growth at low supersaturations (P-LE) with bulk redistribution of manganese, (b) growth at high supersaturations (NP-LE) with negligible partitioning of manganese during transformation. The bulk alloy compositions are designated by the symbol $\bullet$ in each case.

An alternative choice of tie-line could allow $c_2^{\alpha \gamma}\rightarrow \overline{c}_2$ (line cd for alloy B of Figure 1b), so that $\nabla c_2$ is drastically increased since only very small amounts of Mn are partitioned into the austenite. The flux of manganese atoms at the interface correspondingly increases and manganese diffusion can then keep pace with that of carbon, satisfying the mass conservation conditions of equation . The growth of ferrite in this manner is said to occur by a `Negligible Partitioning, Local Equilibrium' (or NPLE) mechanism, in recognition of the fact that the manganese content of the ferrite approximately equals $\overline{c}_2$, so that little if any manganese partitions into austenite.

Paraequilbrium is a constrained equilibrium (Figure 2). It occurs at temperatures where the diffusion of substitutional solutes is not possible within the time scale of the experiment. Nevertheless, intersitials may remain highly mobile. Thus, in a steel, manganese does not partition between the ferrite and austenite, but subject to that constraint, the carbon redistributes until it has the same chemical potential in both phases.

Therefore, the tie-lines in the phase diagram are all virtually parallel to the carbon axis, since Mn does not partition between ferrite and austenite.



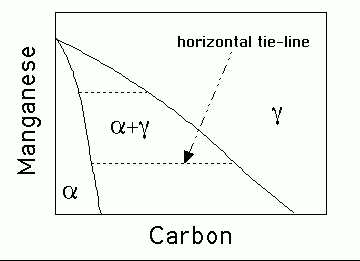
Figure 2: Paraequilibrium phase diagram.



Question 22

(i) What are the crystal structures of the two main allotropic forms ($\alpha$ and $\beta$) of titanium, and which of these two is stable at ambient temperature?

(ii) Sketch the three main kinds of phase diagrams found for titanium alloys given that some solutes stabilise $\alpha$, some stabilise $\beta$ and others are neutral. On the diagram for $\beta$ stabilising elements, construct and justify a curve defining the locus of the martensite-start temperature as a function of the solute concentration.

(iii) Why is the eutectoid reaction found in some titanium alloys so sluggish compared with the formation of pearlite in steels?

(iv) Giving reasons, state typical applications for Ti-Pd and Ti-V-Al alloys.

Answer 22

The high temperature form $\beta$ is body-centered cubic and the low temperature form $\alpha$ is hexagonal close-packed.

The three types of phase diagrams are illustrated below, for $\alpha$, $\beta$ and neutral elements which lead to a eutectoid phase diagram. The locus of $M_S$ temperatures is indicated as a dashed line, with sufficient undercooling to account for strain energy and solute supersaturation.



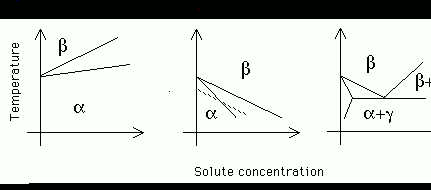
Figure 3: Phase diagrams for titanium.

The eutectoid reaction, for example in the Ti-Cu alloys, involves the solid-state diffusion of substitutional solutes which diffuse at a far smaller rate than intersitial carbon in iron. Consequently, it is frequently possible to avoid the eutectoid reaction by cooling rapidly.

The addition of a small amount ($\simeq 0.2$ wt%) of paladium to titanium makes it much more corrosion resistant in acid. This is because the hydrogen evolution reaction is less polarised (hydrogen evolution is easier), causing the cathodic reaction curve to intersect the cathodic reaction curve in the passive region, leading to a smaller corrosion current (Figure 3).

Ti-6Al-4V is a classic $\alpha+\beta$ alloy with high strength combined with a low density. The $\alpha$ phase is harder and enhances the overall strength, the aluminium helping to stabilise $\alpha$ and lower the density. However, 6Al needs to be balanced by the 4V which is an $\beta$ stabiliser. The alloy is widely used in sheet and forgings for the aerospace industries.



Question 23

Explain why:

(a) martensite, Widmanstätten ferrite and bainite all occur in the form of thin plates;

(b) Widmanstätten ferrite grows at a rate which is much smaller than the speed of sound in the metal;

(c) an Fe-30Ni wt% martensite is weak compared with martensite in Fe-0.2C wt% alloy;

(d) alloying elements have a much greater effect on the kinetics of a reconstructive transformation when compared with the corresponding effect on displacive transformations..

Answer 23

All of these transformations are accompanied by a shape deformation which is an invariant-plane strain (IPS). When elastically accommodated, this causes a strain energy per unit volume given by:

\begin{displaymath}E = {c\over a}\mu(s^2+\delta^2)\end{displaymath}

where $\mu$ is the shear modulus of the austenite and $s$ and $\delta$ are respectively the shear and dilatational components of the IPS. $c/a$ is the thickness to length ratio of the product so that a thin plate shape minimises the strain energy.

Widmanstätten ferrite occurs at temperatures where diffusionless transformation is thermodynamically impossible. Thus, although the change in crystal structure is accomplished by a deformation, the displacements occur at a rate controlled by the diffusion of carbon in the austenite ahead of the interface.

Carbon causes a much greater degree of hardening than any substitutional solute. This is because it leads to a tetragonal distortion of the b.c.c. structure; a tetragonal strain can interact with all components of the stress field of a dislocation. Substitutional solutes cause isotropic strains which can only interact with the small hydrostatic component of stress associated with edge dislocations.

The effect on displacive transformations is thermodynamic alone. On reconstructive transformations the solute may partition between the parent and product phases by a process involving diffusion. This will have a further kinetic effect on reconstructive transformations.



Question 24

A screw dislocation with Burgers vector $[1~1~0]$ glides on the $(\overline 1~1~1)$ plane and intersects another dislocation with Burgers vector $[\overline 1~1~0]$. Can the screw dislocation continue gliding on $(\overline 1~1~1)$ without hinderance?

Answer 24

As a result of the intersection the screw acquires a jog along $[\overline 1~1~0]$, which is the line vector of the jog. The Burgers vector of the jog is still $[1~1~0]$ so that its glide plane is $(0~0~1)$ rendering it sessile on $(\overline 1~1~1)$.



Question 25

Why does ferritic iron change from a ferromagnetic to paramagnetic state as the temperature is raised?

Answer 25

Ferromagnetism involves the alignment of unspinpaired electrons. This is favoured by the accompanying reduction in enthalpy, but there is also an increase in free energy due to a reduction in entropy. As the temperature increases, the free energy increase caused by the reduced entropy of ordering dominates, because it scales with $T$. Hence, magnetic ordering is destroyed, giving paramagnetic iron.



Question 26

Give three essential characteristics of a martensitic transformation. Define an experiment by which each of these characteristics could be measured.

Given that the Bain strain, which changes the face-centered cubic austenite lattice into that of body-centered cubic martensite is an invariant-line strain, explain why the observed shape deformation accompanying martensitic transformation is an invariant-plane strain.

Why is the lattice-invariant deformation unnecessary when austenite transforms by a martensitic mechanism to a hexagonal close-packed lattice?

Why is martensite hard in steels but not so in iron or in non-ferrous metals and alloys?

Answer 26

A martensitic transformation is achieved by a deformation of the parent crystal structure; it therefore leads to a change in shape which can be detected by polishing the parent phase prior to transformation; the shape deformation leads to surface tilts which can be measured using atomic force microscopy, interference optical microscopy or by the deflection of fiducial marks. Martensitic transformations are diffusionless and hence the measured composition of martensite must be the same as that of the parent phase. The interface between martensite and the parent phase must be glissile, i.e. it must be able to move without diffusion. The glissile character can be established by electron microscopy in which the Burgers vectors of the interfacial dislocations are measured and shown to lie out of the plane of the interface (although for pure screws they may lie in the interface plane).

Note that it is not correct to state that the transformation must occur at high speeds or at low temperatures, that it requires rapid quenching or that martensite is hard.

The phenomenological theory of martensite crystallography solves this problem (Figure 4). The Bain strain converts the structure of the parent phase into that of the product phase. When combined with an appropriate rigid body rotation, the net homogeneous lattice deformation ${\bf RB}$ is an invariant-line strain (step $a$ to $c$ in Figure 4). However, the observed shape deformation is an invariant-plane strain ${\bf P_1}$ (step $a$ to $b$ in Figure 4), but this gives the wrong crystal structure. If a second homogeneous shear ${\bf P_2}$ is combined with ${\bf P_1}$ (step $b$ to $c$), then the correct structure is obtained but the wrong shape since

\begin{displaymath}{\bf P_1 P_2 = RB}\end{displaymath}

These discrepancies are all resolved if the shape changing effect of ${\bf P_2}$ is cancelled macroscopically by an inhomogeneous lattice-invariant deformation, which may be slip or twinning as illustrated in Figure 4.

The theory explains all the observed features of the martensite crystallography. The orientation relationship is predicted by deducing the rotation needed to change the Bain strain into an invariant-line strain. The habit plane does not have rational indices because the amount of lattice-invariant deformation needed to recover the correct the macroscopic shape is not usually rational. The theory predicts a substructure in plates of martensite (either twins or slip steps) as is observed experimentally. The transformation goes to all the trouble of ensuring that the shape deformation is macroscopically an invariant-plane strain because this reduces the strain energy when compared with the case where the shape deformation might be an invariant-line strain.



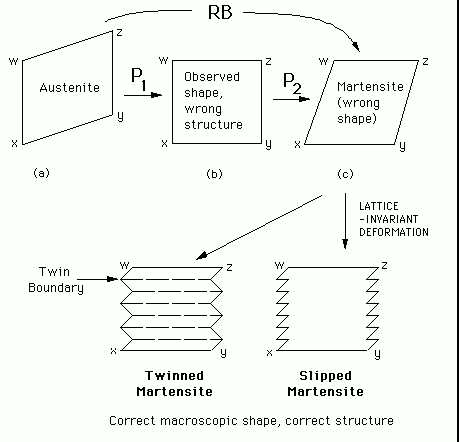
Figure 4: The phenomenological theory of martensite crystallography.

Notice that in the case of the fcc-hcp transformation, the lattice deformation (Bain Strain) itself is an invariant-palne strain, i.e. the motion of Shockley partials on the alternate close-packed planes. B$={\bf P_1}$ so a lattice invariant deformation is not needed. There are no transformation twins or slip steps to be found.

The carbon atom in a b.c.c. lattice causes a tetragonal strain because it resides in an irregular octahedral hole, whose axes are given by the cell edge and two orthogonal face diagonals. A tetragonal strain can interact with both shear and hydrostatic components of stress. Thus, there is a strong interaction with both screw and edge dislocations. By contrast, substitutional solutes (and carbon in austenite) only cause isotropic volume changes which can only interact with the hydrostatic component of stress from edge dislocations, i.e. a weak interaction.



Question 27

(i) What are the mechanisms by which an ordered precipitate, which is coherent with the matrix, may strengthen an alloy?

(ii) Explain the cause of precipitate-free zones and how they might be avoided.

(iii) Why are aluminium-silicon alloys good as casting alloys? How might their microstructures be improved?

Answer 27

Order hardening, because pairs of dislocations have to enter the ordered phase. Also, modulus hardening since the energy per unit length of a dislocation depends on the shear modulus of the crystal. The modulus is likely to be different for the matrix and precipitate phases.

It is possible, at large driving forces, for precipitates to nucleate homogeneously. However, it is more common for nucleation to occur heterogeneously because there is a gain in energy as the defect on which the particle forms is partly or wholly eliminated.

Vacancies are a prominent nucleation site for many precipitates, particularly in aluminium alloys where the concentration of vacancies tends to be high. However, there is a vacancy denuded zone next to a grain boundary (which is a sink for vacancies), Figure 5. There will, therefore, be a precipitate-free zone (PFZ) adjacent to a grain boundary.





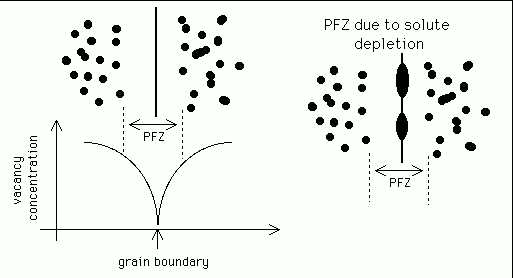
Figure 5: Precipitate-free zones.

An alternative reason for PFZ formation is that nucleation happens first on grain boundaries which are themselves potent nucleation sites. These precipitates drain the adjacent matrix from solute and hence a solute depleted PFZ arises, with coarse particles at the boundaries.

Precipitate-free zones can be eliminated by a two-stage heat treatment where nucleation is induced homogeneously at a low temperature, and the precipitates are then allowed to grow at a higher temperature (Figure 6). Thus, for Al-6Zn-3Mg age-hardening alloy, GP zones are used as nuclei for the $\eta$ (${\rm MgZn_2})$ phase.

twostage22294400Figure 6: Two-stage heat treatment

Aluminium casting alloys closely resemble cast irons. Aluminium-12 wt% silicon eutectic compositions are frequently used because this gives the minimum melting temperature. The silicon which has a density of just 2.34 $\,{\rm g\,cm^{-3}}$, precipitates virtually as pure silicon. The resulting expansion compensates for freezing contractions to give castings with minimal porosity.

The silicon is coarse and brittle. The addition of a minute quantity of sodium (0.02 wt%) greatly refines the Si particles giving a higher toughness. It does so by removing P; AlP is a good nucleant for Si so its removal allows solidification to occur at a higher undercooling, where the nucleation rate can be larger.



Question 28

(a) Explain why the addition of a small amount of palladium to titanium can improve its corrosion resistance in oxidising solutions.

(b) Explain why the most popular titanium alloy contains both aluminium and vanadium as alloying additions.

(c) Giving one example, explain what is meant by solute trapping.

(d) Distinguish between martensite, lower bainite, upper bainite and Widmanstätten ferrite.

Answer 28

Pure titanium has excellent resistance to corrosion and is used widely in the chemical industries. There is a passive oxide film which makes it particularly resistant to corrosion in oxidising solution. The corrosion resistance can be further improved by adding palladium (0.15 wt%), which makes hydrogen evolution easier at cathodic sites so that the anodic and cathodic reactions balance in the passive region (Figure 6).



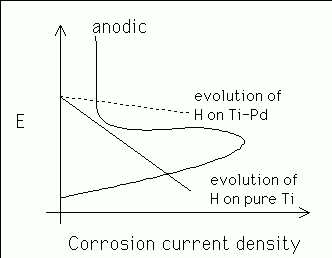
Figure 6: Corrosion of Ti and Ti-Pd.

Aluminium reduces the density of Ti and stabilizes and strengthens the $\alpha$ phase while vanadium provides a greater amount of more ductile $\beta$ phase during hot-working.

Solute is said to be trapped when its chemical potential increases on transfer across the moving interface. It occurs when the interface velocity becomes comparable to the diffusion velocity $(D/\lambda)$ wheere $\lambda$ is the interatomic jump distance. Examples: rapid solidification, martensitic transformation (C in Fe), paraequilibrium (Mn in ferrite).

Martensitic transformation is diffusionless. Bainite grows without diffusion but because it forms at relatively high temperatures, the carbon can rapidly (a second or so) escape into the residual austenite. It may then precipitate as cementite, giving an upper bainite microstructure. If the bainite transformation temperature is reduced then the carbon escapes less rapidly so that it is possible for some of it to precipitate inside the ferrite plates, giving a lower bainite microstructure (Fig. 6.12, Honeycombe & Bhadeshia). Widmanstätten ferrite grows by a displacive paraequilibrium mechanism involving the diffusion of carbon. It thus grows at a rate which is controlled by the diffusion of carbon in the austenite ahead of the interface. Furthermore, there is little driving force available at the temperatures at which Widmanstätten ferrite grows so two plates have to grow together in a self-accommodating manner in order to reduce the overall strain energy. This is why it optically appears to be in the form of a thin wedge, since the component plates have slightly different habit planes.



Question 29

What is an ideal solution? What is the probability of finding an $A$ atom next to a $B$ atom in an equiatomic ideal solution?

Answer 29

An ideal solution is one where the enthalpy of mixing is zero. This means that $A$ atoms are indifferent to who their neighbours are. The atoms are dispersed at random, so that

\begin{displaymath}p_{AB} = 2\times 0.5\times 0.5 = 0.5 \end{displaymath}


Worked Examples 1-4
Worked Examples 5-13
Worked Examples 14-20

H.K.D.H. Bhadeshia
2000-06-09