Part II Metals and Alloys

Course C9: Worked Examples (30-37)

H. K. D. H. Bhadeshia

Download Postscript file
Download PDF file

Worked Examples 1-4
Worked Examples 5-13
Worked Examples 14-20
Worked Examples 21-29

Question 30

Upper bainite in conventional steels consists of a mixture of bainitic ferrite and cementite. How can this cementite be eliminated from the microstructure?

When the precipitation of cementite is prevented, the microstructure obtained by isothermal transformation in the bainite temperature range consists of just bainitic ferrite and carbon-enriched retained austenite. State four potential advantages of this microstructure from the point of view of toughness and strength.

One difficulty with the mixed microstructure of bainitic ferrite and retained austenite is that the austenite, when present in large quantities, is unstable and hence forms high-carbon, brittle martensite. Explain three ways in which this problem can be eliminated.

Answer 30

Silicon has an incredibly small solubility in cementite. Therefore, increasing the silicon concentration of a steel to a value greater than about 1.5 wt% ensures the absence of cementite in upper bainite. Aluminium and to a lesser extent chromium, have the same effect. Note that silicon has a similar effect in cast irons. (20%)

The six potential advantages (only four required in the answer) of the microstructure can be listed as follows: (40%)

1. Cementite is responsible for initiating fracture in high-strength steels. Its absence is expected to make the microstructure more resistant to cleavage failure and void formation.
2. The bainitic ferrite is almost free of carbon, which intensely strengthens ferrite and hence embrittles it.
3. The microstructure derives its strength from the fine grain size of the ferrite plates, which are less than 1 in thickness. It is the thickness of these plates which determines the mean free slip distance, so that the effective grain size is less than a micrometer. This cannot be achieved by any other commercially viable process. Grain refinement is the only method available for simultaneously improving the strength and toughness of steels.
4. The ductile films of austenite which are intimately dispersed between the plates of ferrite have a crack blunting effect. They further add to toughness by increasing the work of fracture as the austenite is induced to transform to martensite under the influence of the stress field of a propagating crack. This is the TRIP, or transformation-induced plasticity effect.
5. The diffusion of hydrogen in austenite is slower than in ferrite. The presence of austenite can therefore improve the stress corrosion resistance of the microstructure.
6. Steels with the bainitic ferrite and austenite microstructure can be obtained without the use of expensive alloying. All that is required is that the silicon concentration should be large enough to suppress cementite.

The problem of unstable retained austenite arises because the amount of bainite that can form is limited by the $T_0$ curve on the phase diagram. Therefore, the three ways all relate to the $T_0$ curve, as follows: (40%)

1. By reducing the isothermal transformation temperature to increase $x_{T_0}$. The lower limit is set by either the lower bainite or martensite-start temperature.
2. By reducing the overall carbon concentration of the steel, so that the austenite reaches its limiting composition at a later stage of reaction.
3. By moving the $T_0$ curves of the phase diagram to larger carbon concentrations. This can be done by adjusting the concentration and type of substitutional solute (a).

Queston 31

Explain why martensite grows in the form of thin plates.

Answer 31

The shape deformation accompanying the growth of martensite is an invariant-plane strain with a large shear component. The shear strain is typically $s=0.25$, with a dilatational strain of about $\delta=0.03$ normal to the habit plane. The strain energy per unit volume of martensite is given by (thickness $c$ and length $r$) is given by:

$$E={c\over r}\mu(s^2+\delta^2)$$

where $\mu$ is the shear modulus of the parent phase. It follows that this strain energy is minimised by adopting a plate shape. Another way of looking at this is illustrated in the figure below. The absolute magnitude of the displacements gets larger as the product gets thicker in the direction normal to the habit plane (compare displacements at a and b. Therefore, the thinner the plate, the smaller the absolute displacements that have to be accommodated.

Question 32

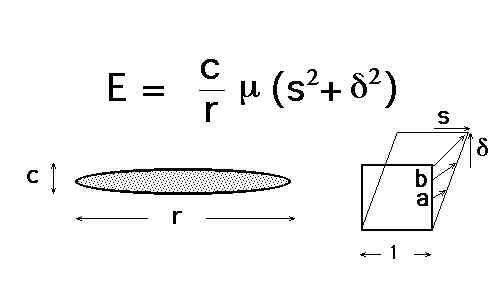
Explain what is meant by the term paraequilibrium. Illustrate schematically an isothermal section of the paraequilibrium phase diagram for an Fe-Mn-C alloy where austenite and ferrite can coexist. The sketch should include tie-lines.

Why does the austenite$+$ferrite phase field converge to a point when the carbon concentration becomes zero?

Define in thermodynamic terms, what is meant when an element is said to be trapped during transformation.

During the paraequilibrium growth of ferrite in an Fe-Mn-C alloy, which of the elements is trapped in the ferrite, and which in austenite?

Answer 32

Paraequilibrium is a constrained equilibrium. It occurs at temperatures where the diffusion of substitutional solutes is not possible within the time scale of the experiment. Nevertheless, interstitials may remain highly mobile. Thus, in a steel, manganese does not partition between the ferrite and austenite, but subject to that constraint, the carbon redistributes until it has the same chemical potential in both phases. (40%)

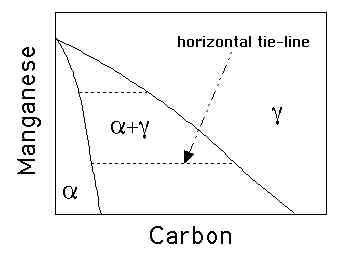
Therefore, the tie-lines in the phase diagram are all virtually parallel to the carbon axis, since Mn does not partition between ferrite and austenite. (20%)

At zero carbon concentration, the austenite and ferrite have exactly the same chemical composition since Mn does not redistribute during transformation. Therefore, there is a unique concentration at which the two phases have equal free energy, they are in equilibrium. (10%)

An element is said to be trapped when its chemical potential increases on transfer across the moving interface. (10%)

The manganese is trapped in the ferrite since its chemical potential increases on transfer across the interface, the iron is trapped in the austenite for the same reason. Manganese is an austenite stabiliser so its equilibrium concentration in austenite should be greater than that in ferrite. (20%)

Question 33

Describe the characteristics of the $\beta\rightarrow\omega$ transformation in some titanium or zirconium alloys and explain the mechanism of the transformation.

How would the transformation manifest in an electron diffraction pattern?

Describe any other diffusionless transformation possible in titanium alloys and state the observed orientation relationship.

How would you represent the temperature below which diffusionless transformation becomes thermodynamically possible on a phase diagram for a binary titanium alloy?

Answer 33

$\omega$ is a metastable phase which forms from $\beta$ in alloys based on titanium, zirconium and hafnium. It is important because its formation generally leads to a deterioration in the mechanical properties. In Ti-Nb alloys its formation influences superconduction. The transformation to $\omega$ is diffusionless, occurs below the $T_0$ temperature and frequently cannot be suppressed even by quenching at 11000 ${\rm\,C\,s^{-1}}$. Its presence causes diffuse streaking in the electron diffraction patterns of the $\beta$ phases. The streaks become more intense and curved as the temperature or the solute concentration increases. There is also an increase in the electrical resistance as $\omega$ forms.

The $\beta\rightleftharpoons\omega$ transformation is reversible and diffusionless but is not martensitic in the classical sense since there is no invariant-plane strain shape deformation. However, it does involve the coordinated motion of atoms.

The body-centred cubic (bcc) crystal structure of $\beta$ can be imagined as the stacking of $\{111\}_\beta$ planes in an $....ABCABC....$ stacking sequence. Note that these planes are not close-packed in the bcc structure. The $\beta\rightleftharpoons\omega$ transformation occurs by the passage of a longitudinal displacement wave along $<111>$ which causes the $B$ and $C$ planes to collapse into each other, leaving the $A$ planes unaffected. The stacking sequence thus changes to $...AB'AB'AB'....$ in which the $B'$ planes have twice the density of atoms as the $A$ planes. The $...AB'AB'AB'....$ stacking is consistent with a $\omega$ a hexagonal crystal structure with a $c/a \simeq 0.6$. The atoms in the $B'$ plane have a trigonal coordination which is similar to that in graphite and the bonding becomes partly covalent. (60%)

This leads to an increase in the electrical resistivity. The longitudinal displacement waves are responsible for the streaking in the electron diffraction patterns. (10%)

Quenching the $\beta$ phase leads to the formation of h.c.p. $\alpha'$ martensite. The orientation relationship is with the most densly packed planes parallel and the corresponding most densly packed directions parallel (the relationship is actually irrational, so the stated orientation is approximate).

$$(1~1~0)_\beta \paral (0~0~0~1)_{\alpha'} \qquad [1~\overline 1~1]_\beta \paral [1~1~\overline 2~0]_{\alpha'}$$

and the habit plane of the martensite is close to $\{3~3~4\}_\beta$. (20%)

The temperature is represented by the $T_0$ curve.

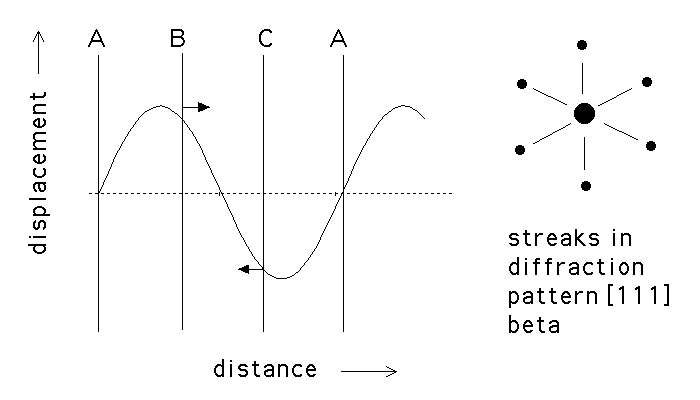
(a) Displacement wave associated with the $\beta$ to $\omega$ transformation. The $A$ planes are unaffected since they lie at the nodes. (b) Streaks in the electron diffraction pattern during the $\omega$ transformation.

Question 34

Give three features of martensite that distinguish it from a reconstructive transformation such as allotriomorphic ferrite. Explain how you might characterise each of these features using experiments.

Giving reasons, explain which of the following deformations is an invariant-plane strain

• simultaneous slip on two independent slip systems;
• mechanical twinning;
• elastic elongation of a material with a zero Poisson's ratio;
• hydrostatic expansion.

Show diagrammatically that it is not possible to transform austenite into body-centred cubic martensite by a deformation which is an invariant plane strain.

Why is martensite hard in steels but not so in iron or in other non-ferrous metals and alloys?

Answer 34

A martensitic transformation is achieved by a deformation of the parent crystal structure; it therefore leads to a shape deformation which has a large shear component, and which can be detected by polishing the parent phase prior to transformation. The shape deformation causes surface tilts which can be measured using atomic force microscopy, interference optical microscopy or by the deflection of fiducial marks. The formation of allotriomorphic ferrite is not accompanied by any shear strain, simply a small volume change which does not deflect any fiducial marks.

Martensitic transformations are diffusionless and hence the measured composition of martensite must always be the same as that of the parent phase. The chemical composition of allotriomorphic ferrite corresponds to its equilibrium composition and hence in general will differ from that of the parent phase. The chemical composition can be measured using energy dispersive X-ray microanalysis, the atom-probe technique and X-ray diffraction.

The interface between martensite and the parent phase must be glissile, it must be able to move without diffusion. The glissile character can be established by electron microscopy in which the Burgers vectors of the interfacial dislocations are measured and shown to lie out of the plane of the interface (although for pure screws they may lie in the interface plane). There are no such requirements for the structure of the interface between allotriomorphic ferrite and austenite (it may be sessile or glissle, and will always require diffusion in order to translate).

Note that it is not correct to state that the transformation must occur at high speeds or at low temperatures, that it requires rapid quenching or that martensite is hard. Martensite can be soft, slow, and can take place at high temperatures.

• slip is an invariant-plane strain (IPS), but the simultaneous operation of slip on two non-parallel planes leaves only the line of intersection undeformed and unrotated. This deformation is therefore an invariant-line strain;
• mechanical twinning is a shear on a plane which remains invariant (an IPS);
• elastic elongation of a material with a zero Poisson's ratio is also an IPS since the deformation is only normal to the invariant-plane. Beryllium has virtually a zero Poisson's ratio;
• hydrostatic expansion distorts all vectors and hence is not an IPS.

Suppose that the austenite is represented as a sphere with its unit cell edges denoted by the vectors ${\bf a_i}$ with $i=1,2,3$, as illustrated in a,b. The Bain strain changes the sphere into an ellipsoid of revolution about ${\bf a_1}$. There are no lines in the $(0~0~1)_\gamma$ plane which are undistorted. However, it is possible to find lines such as $wx$ and $yz$ are undistorted by the deformation, but are rotated to the new positions $w'x'$ and $y'z'$. Since they are rotated by the Bain deformation they are not invariant-lines. In fact, the Bain strain does not produced an invariant-line strain. It can be converted into an invariant-line strain by adding a rigid body rotation as illustrated in c. The rotation reorients the $\alpha'$ lattice but has no effect on its crystal structure. The effect of the rotation is to make one of the original undistorted lines (in this case $yz$) invariant so that the total effect BR of the Bain strain B and the rotation R is indeed an invariant-line strain. This is the reason why the observed irrational orientation relationship (KS/NW type) differs from that implied by the Bain strain. The rotation required to generate convert B to an ILS precisely predicts the observed orientation from the Bain orientation.

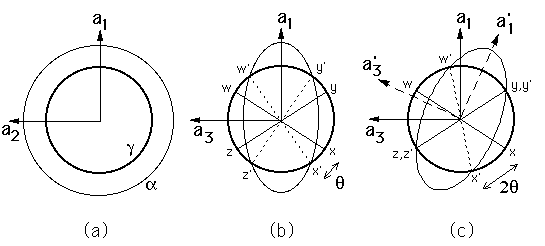
(a) and (b) show the effect of the Bain strain on austenite, which when undeformed is represented as a sphere of diameter $wx=yz$ in three-dimensions. The strain transforms it to an ellipsoid of revolution. (c) shows the invariant-line strain obtained by combining the Bain strain with a rigid body rotation.

It is also apparent from (c) that there is no possible rotation which would convert B into an invariant-plane strain because there is no rotation capable of making two of the non-parallel undistorted lines into invariant-lines. Thus, it is impossible to convert austenite into $\alpha'$ martensite by a strain which is an invariant-plane strain. A corollary to this statement is that the two crystals cannot ever be joined at an interface which is fully coherent and stress-free.

The carbon atom in a b.c.c. lattice causes a tetragonal strain because it resides in an irregular octahedral hole, whose axes are given by the cell edge and two orthogonal face diagonals. A tetragonal strain can interact with both shear and hydrostatic components of stress. Thus, there is a strong interaction with both screw and edge dislocations. By contrast, substitutional solutes (and carbon in austenite) only cause isotropic volume changes which can only interact with the hydrostatic component of stress from edge dislocations, a weak interaction.

Question 35

Describe the roles of aluminium and vanadium in Ti-6Al-4V alloy. Why should the use of this alloy in an aeroengine be limited to temperatures less than about 400^oC?

Answer 35

Al reduces density, stabilises and strengthens $\alpha$ while vanadium provides a greater a mount of the more ductile $\beta$ phase for hot-working. This alloy is very commonly used because of its strength (1100 MPa), creep resistance at 300 , fatigue resistance and castability. Common titanium alloys have low densities and can be creep resistant. However, titanium fires can occur when titanium components accidentally rub against other metals when the temperature of the environment is greater than about 400.

Question 36

Explain what is meant by the term paraequilibrium. Illustrate schematically an isothermal section of the paraequilibrium phase diagram for an Fe-Mn-C alloy where austenite and ferrite can coexist. The sketch should include tie-lines with an explanation of how you construct them.

Explain the mechanism of the transformation in steels, including a description of the factors that determine its growth rate and shape.

Which solute is said to be trapped in the product phase during transformation of austenite in a Fe-Mn-C alloy, in the following cases:

• the growth of Widmanstatten ferrite;
• the growth of martensite.

Answer 36

Paraequilibrium is a constrained equilibrium. It occurs at temperatures where the diffusion of substitutional solutes is not possible within the time scale of the experiment. Nevertheless, interstitials may remain highly mobile. Thus, in a steel, manganese does not partition between the ferrite and austenite, but subject to that constraint, the carbon redistributes until it has the same chemical potential in both phases.

Therefore, the tie-lines in the phase diagram are all virtually parallel to the carbon axis, since Mn does not partition between ferrite and austenite.

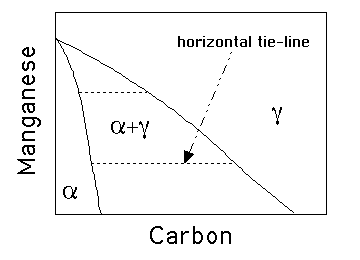
Widmanstatten ferrite grows by a displacive paraequilibrium mechanism involving the diffusion of carbon. It thus grows at a rate which is controlled by the diffusion of carbon in the austenite ahead of the interface. Furthermore, there is little driving force available at the temperatures at which the ferrite grows so two plates have to grow together in a self-accommodating manner in order to reduce the overall strain energy. This is why it optically appears to be in the form of a thin wedge, since the component plates have slightly different habit planes.

• manganese; carbon partitions during the paraequilibrium growth of Widmanstatten ferrite;
• both carbon and manganese since martensitic transformations are diffusionless.

Question 37

Prove that the solubility of solute in an aluminium alloy containing copper is greater when the matrix is in equilibrium with a metastable precipitate such as GP1, when compared with the case where it is in equilibrium with the stable precipitate CuAl$_2$.

Assuming that the Al-Cu solution can be described by a regular solution thermodynamic model, show that the solubility $x$ of solute in the matrix varies as follows:

$$x =\exp\bl\{-{{z\omega}\over{kT}} \br\}$$

Note that the molar free energy of mixing is

$$\Delta G_M = N_a z(1-x)x\omega + N_a kT[(1-x)\ln\{1-x\} + x\ln\{x\}]$$

where $N_a$ is Avogadro's number, $k$ is the Boltzmann constant, $T$ is the absolute temperature and $\omega$ is positive for the Al-Cu system.

Would you expect the copper atoms to cluster or to order at low temperatures?

Answer 37

The solubility of solute in the matrix $(\alpha)$ is therefore of importance. This solubility cannot be defined in isolation - it depends on the phase with which the $\alpha$ is in equilibrium with, . In the Al-Cu system, the stable precipitate is CuAl$_2$ but because it is difficult to nucleate, metastable GP1 zones form first. Thus, the free energy curve for GP1 zones is located above that for CuAl$_2$ in b. The common tangent construction shows that this leads to an increase in the solubility of copper in $\alpha$ when it is in equilibrium with GP1 zones. Another interpretation is that a greater undercooling is required before GP1 zones can precipitate.

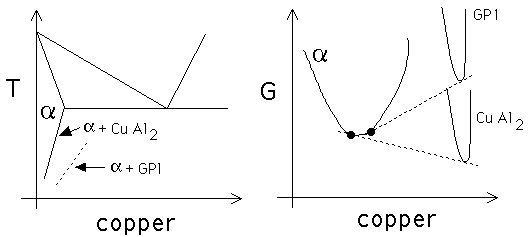
(a) The solubility of solute in $\alpha$ is larger when it is in equilibrium with GP1 zones compared with when it is in equilibrium with CuAl$_2$. (b) This can be justified using free energy diagrams.

Since $\omega$ is positive, so is the enthalpy of mixing $\Delta H_M$. The free energy versus composition plot will therefore have two minima at low temperatures. The minimum at lower concentrations gives the solubility in matrix, it is safe to assume $x\ll 1$.

The miscibility gap at any temperature can be determined by the usual common tangent construction on the free energy curve with the two minima. Noting that the regular solution model has symmetry about $x=0.5$, the compositions corresponding to the common tangent construction can in this special case be obtained by setting

$${{\partial \Delta G_M}\over{\partial x}} =0$$

that is,

$$N_az(1-2x)\omega + N_akT \ln{{x}\over{1-x}} = 0$$

which in the limit of small $x$ gives

$$x =\exp\bl\{-{{z\omega}\over{kT}} \br\}$$

The solubility therefore changes exponentially with the reciprocal of temperature, and increases as $\Delta H_M$ tends to zero. A positive enthalpy of mixing indicates a tendency for clustering.