Part II Metals and Alloys
Course C9: Worked Examples (30-33)

H. K. D. H. Bhadeshia

Download Postscript file
Download PDF file

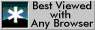
Worked Examples 1-4
Worked Examples 5-13
Worked Examples 14-20
Worked Examples 21-29

Question 30

Upper bainite in conventional steels consists of a mixture of bainitic ferrite and cementite. How can this cementite be eliminated from the microstructure?

When the precipitation of cementite is prevented, the microstructure obtained by isothermal transformation in the bainite temperature range consists of just bainitic ferrite and carbon-enriched retained austenite. State four potential advantages of this microstructure from the point of view of toughness and strength.

One difficulty with the mixed microstructure of bainitic ferrite and retained austenite is that the austenite, when present in large quantities, is unstable and hence forms high-carbon, brittle martensite. Explain three ways in which this problem can be eliminated.

Answer 30

Silicon has an incredibly small solubility in cementite. Therefore, increasing the silicon concentration of a steel to a value greater than about 1.5 wt% ensures the absence of cementite in upper bainite. Aluminium and to a lesser extent chromium, have the same effect. Note that silicon has a similar effect in cast irons. (20%)

The six potential advantages (only four required in the answer) of the microstructure can be listed as follows: (40%)

1. Cementite is responsible for initiating fracture in high-strength steels. Its absence is expected to make the microstructure more resistant to cleavage failure and void formation.
2. The bainitic ferrite is almost free of carbon, which intensely strengthens ferrite and hence embrittles it.
3. The microstructure derives its strength from the fine grain size of the ferrite plates, which are less than 1 in thickness. It is the thickness of these plates which determines the mean free slip distance, so that the effective grain size is less than a micrometer. This cannot be achieved by any other commercially viable process. Grain refinement is the only method available for simultaneously improving the strength and toughness of steels.
4. The ductile films of austenite which are intimately dispersed between the plates of ferrite have a crack blunting effect. They further add to toughness by increasing the work of fracture as the austenite is induced to transform to martensite under the influence of the stress field of a propagating crack. This is the TRIP, or transformation-induced plasticity effect.
5. The diffusion of hydrogen in austenite is slower than in ferrite. The presence of austenite can therefore improve the stress corrosion resistance of the microstructure.
6. Steels with the bainitic ferrite and austenite microstructure can be obtained without the use of expensive alloying. All that is required is that the silicon concentration should be large enough to suppress cementite.

The problem of unstable retained austenite arises because the amount of bainite that can form is limited by the $T_0$ curve on the phase diagram. Therefore, the three ways all relate to the $T_0$ curve, as follows: (40%)

1. By reducing the isothermal transformation temperature to increase $x_{T_0}$. The lower limit is set by either the lower bainite or martensite-start temperature.
2. By reducing the overall carbon concentration of the steel, so that the austenite reaches its limiting composition at a later stage of reaction.
3. By moving the $T_0$ curves of the phase diagram to larger carbon concentrations. This can be done by adjusting the concentration and type of substitutional solute (a).

Queston 31

Explain why martensite grows in the form of thin plates.

Answer 31

The shape deformation accompanying the growth of martensite is an invariant-plane strain with a large shear component. The shear strain is typically $s=0.25$, with a dilatational strain of about $\delta=0.03$ normal to the habit plane. The strain energy per unit volume of martensite is given by (thickness $c$ and length $r$) is given by:

$$E={c\over r}\mu(s^2+\delta^2)$$

where $\mu$ is the shear modulus of the parent phase. It follows that this strain energy is minimised by adopting a plate shape. Another way of looking at this is illustrated in the figure below. The absolute magnitude of the displacements gets larger as the product gets thicker in the direction normal to the habit plane (compare displacements at a and b. Therefore, the thinner the plate, the smaller the absolute displacements that have to be accommodated.

Question 32

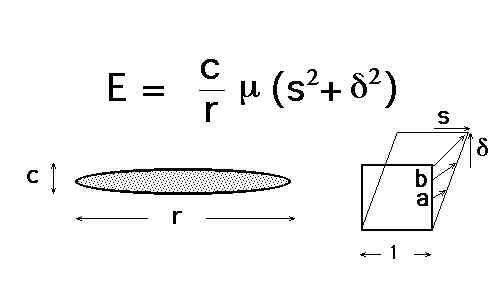
Explain what is meant by the term paraequilibrium. Illustrate schematically an isothermal section of the paraequilibrium phase diagram for an Fe-Mn-C alloy where austenite and ferrite can coexist. The sketch should include tie-lines.

Why does the austenite$+$ferrite phase field converge to a point when the carbon concentration becomes zero?

Define in thermodynamic terms, what is meant when an element is said to be trapped during transformation.

During the paraequilibrium growth of ferrite in an Fe-Mn-C alloy, which of the elements is trapped in the ferrite, and which in austenite?

Answer 32

Paraequilibrium is a constrained equilibrium. It occurs at temperatures where the diffusion of substitutional solutes is not possible within the time scale of the experiment. Nevertheless, interstitials may remain highly mobile. Thus, in a steel, manganese does not partition between the ferrite and austenite, but subject to that constraint, the carbon redistributes until it has the same chemical potential in both phases. (40%)

Therefore, the tie-lines in the phase diagram are all virtually parallel to the carbon axis, since Mn does not partition between ferrite and austenite. (20%)

At zero carbon concentration, the austenite and ferrite have exactly the same chemical composition since Mn does not redistribute during transformation. Therefore, there is a unique concentration at which the two phases have equal free energy, they are in equilibrium. (10%)

An element is said to be trapped when its chemical potential increases on transfer across the moving interface. (10%)

The manganese is trapped in the ferrite since its chemical potential increases on transfer across the interface, the iron is trapped in the austenite for the same reason. Manganese is an austenite stabiliser so its equilibrium concentration in austenite should be greater than that in ferrite. (20%)

Question 33

Describe the characteristics of the $\beta\rightarrow\omega$ transformation in some titanium or zirconium alloys and explain the mechanism of the transformation.

How would the transformation manifest in an electron diffraction pattern?

Describe any other diffusionless transformation possible in titanium alloys and state the observed orientation relationship.

How would you represent the temperature below which diffusionless transformation becomes thermodynamically possible on a phase diagram for a binary titanium alloy?

Answer 33

$\omega$ is a metastable phase which forms from $\beta$ in alloys based on titanium, zirconium and hafnium. It is important because its formation generally leads to a deterioration in the mechanical properties. In Ti-Nb alloys its formation influences superconduction. The transformation to $\omega$ is diffusionless, occurs below the $T_0$ temperature and frequently cannot be suppressed even by quenching at 11000 ${\rm\,C\,s^{-1}}$. Its presence causes diffuse streaking in the electron diffraction patterns of the $\beta$ phases. The streaks become more intense and curved as the temperature or the solute concentration increases. There is also an increase in the electrical resistance as $\omega$ forms.

The $\beta\rightleftharpoons\omega$ transformation is reversible and diffusionless but is not martensitic in the classical sense since there is no invariant-plane strain shape deformation. However, it does involve the coordinated motion of atoms.

The body-centred cubic (bcc) crystal structure of $\beta$ can be imagined as the stacking of $\{111\}_\beta$ planes in an $....ABCABC....$ stacking sequence. Note that these planes are not close-packed in the bcc structure. The $\beta\rightleftharpoons\omega$ transformation occurs by the passage of a longitudinal displacement wave along $<111>$ which causes the $B$ and $C$ planes to collapse into each other, leaving the $A$ planes unaffected. The stacking sequence thus changes to $...AB'AB'AB'....$ in which the $B'$ planes have twice the density of atoms as the $A$ planes. The $...AB'AB'AB'....$ stacking is consistent with a $\omega$ a hexagonal crystal structure with a $c/a \simeq 0.6$. The atoms in the $B'$ plane have a trigonal coordination which is similar to that in graphite and the bonding becomes partly covalent. (60%)

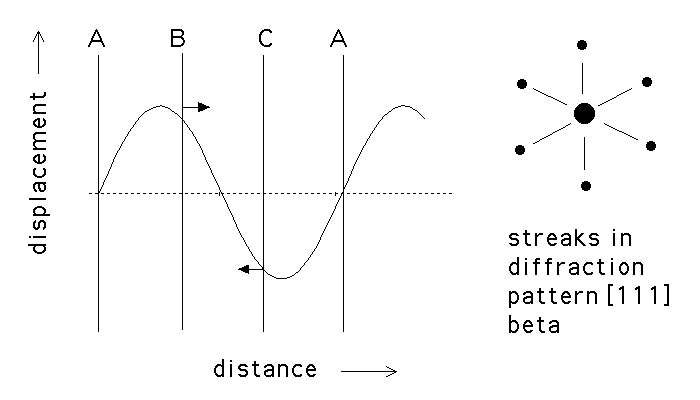
This leads to an increase in the electrical resistivity. The longitudinal displacement waves are responsible for the streaking in the electron diffraction patterns. (10%)

omega237144 350: (a) Displacement wave associated with the $\beta$ to $\omega$ transformation. The $A$ planes are unaffected since they lie at the nodes. (b) Streaks in the electron diffraction pattern during the $\omega$ transformation.

Quenching the $\beta$ phase leads to the formation of h.c.p. $\alpha'$ martensite. The orientation relationship is with the most densly packed planes parallel and the corresponding most densly packed directions parallel (the relationship is actually irrational, so the stated orientation is approximate).

$$(1~1~0)_\beta \paral (0~0~0~1)_{\alpha'} \qquad [1~\overline 1~1]_\beta \paral [1~1~\overline 2~0]_{\alpha'}$$

and the habit plane of the martensite is close to $\{3~3~4\}_\beta$. (20%)

The temperature is represented by the $T_0$ curve.