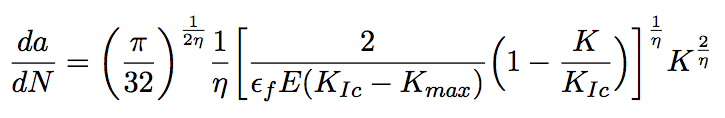
Fatigue Crack Growth Rate Model for Metallic Alloys

R. C. Dimitriu and H. K. D. H. Bhadeshia

Abstract

A model has been created to allow the quantitative estimation of the fatigue crack growth rate in steels as a function of mechanical properties, test-specimen characteristics, stress-intensity range and test–frequency. With this design, the remarkable result is that the method which is based on steels, can be used without modification, and without any prior fatigue test, to estimate the crack growth rates in nickel, titanium and aluminium alloys. It appears therefore that a large proportion of the differences in the fatigue crack growth rate of metallic alloys can be explained in terms of the macroscopic tensile properties of the material rather than the details of the microstructure and chemical composition.

Materials and Design, 31 (2010) 2134-2139.

Download paper

fatigue crack growth

Related Paper



Fatigue Crack Growth Rate Model for Metallic Alloys

R. C. Dimitriu and H. K. D. H. Bhadeshia

University of Cambridge
Materials Science and Metallurgy
Pembroke Street, Cambridge CB2 3QZ, U. K.


Abstract

A model has been created to allow the quantitative estimation of the fatigue crack growth rate in steels as a function of mechanical properties, test-specimen characteristics, stress-intensity range and test-frequency. With this design, the remarkable result is that the method which is based on steels, can be used without modification, and without any prior fatigue test, to estimate the crack growth rates in nickel, titanium and aluminium alloys. It appears therefore that a large proportion of the differences in the fatigue crack growth rate of metallic alloys can be explained in terms of the macroscopic tensile properties of the material rather than the details of the microstructure and chemical composition.

Keywords: Fatigue Crack Growth, Neural Network, Steel, Superalloys, Titanium Alloys, Aluminium Alloys

Introduction

It is understood that fatigue crack growth is a consequence of the accumulation of damage by deformation in the plastic zone at the crack tip. At low loads the deformation is governed by the cyclic variation in the stress-intensity range $ \Delta K$. The crack extension per cycle $ (da/dN)$ becomes measurable at a threshold $ \Delta K_{th}$, followed by the slower extension rate in the Paris Law regime [4,2,1,3] described by the proportionality

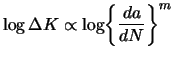$\displaystyle \log \Delta K \propto \log \biggl\{\frac{da}{dN}\biggr\}^m$ (1)

where $ da/dN$ is the average crack advance per cycle, and $ m$ is known as the Paris exponent. The equation can be interpreted in terms of a variety of physical mechanisms [5,6], in which case the proportionality constant ($ C$) becomes a function of the Young's Modulus $ E$, the Poisson's ratio $ \nu$, and the yield and ultimate tensile strengths $ \sigma_Y$ and $ \sigma_U$ respectively. Based on the possible mechanisms consistent with the Paris Law, attempts have been made to generally interpret fatigue crack growth data on the basis of just the mechanical properties of the material [5,6].

Elber modified the relation with an effective stress intensity range $ \Delta K_{eff}$ to allow for variable amplitude loading, arguing that cracks grow only when their tips are open [7]:

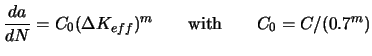$\displaystyle \frac{da}{dN} = C_{0}(\Delta K_{eff})^m \qquad\hbox{with}\qquad C_0=C/(0.7^m)$ (2)

These equations do not explicitly contain material properties; Duggan [8] expressed the crack growth rate in terms of the elastic modulus, toughness, and ductility:
$\displaystyle \frac{da}{dN} = \bigg( \frac{\pi}{32} \bigg)^{\frac{1}{2\eta}} \f... ... ) } \Big(1 - \frac{K}{K_{Ic}} \Big) \bigg]^{\frac{1}{\eta}} K^{\frac{2}{\eta}}$ (3)

where $ \eta$ and $ \epsilon$ are the fatigue ductility exponent and coefficient respectively, $ E$ is the elastic modulus, $ K_{Ic}$ is the critical stress intensity for fracture. Ramsamooj and Shugar have also accounted for toughness, yield strength and modulus, but not for frequency and the analysis is presumably limited to mode I loading [9]. Their model is interesting in that it generalises against iron, aluminium and titanium alloys; it does however require a prior knowledge of the threshold stress intensity range for fatigue crack growth.

The aim here was to exploit published fatigue crack growth data to create a model based on physical variables which are readily measured in a tensile test, rather than rely on inputs which depend on fatigue testing, and further, to include variables which account for test-specimen parameters. The model uses neural network analysis; although there are physically based models available in the literature, for example, [10], they require fitting parameters; a neural network is the most general way of achieving fitting without making prior assumptions about the relationship to which the data are fitted [11]. There have been other attempts to use neural networks for this purpose [12] but they do not adequately treat the uncertainties of modelling so it is not possible to properly assess the predictions made. The original intention here was to study steels, but as will be seen later, the model was, without modification, found to generalise to other alloy systems.

Method

A versatile method for treating empirical data is the neural network in a Bayesian framework. The theory behind practical Bayesian networks has been described in [14,13] and the background information theory is available in a seminal textbook on the subject [15]. In addition, this method been reviewed thoroughly [11], as have been its applications [16]. Indeed, there have been diverse applications which lead to useful and verifiable predictions in the context of low-cycle fatigue [17], the estimation of bainite plate thickness [18], the calculation of ferrite number in stainless steels [19], the estimation of tensile strength [20,27], impact strength [26,21], the effect of processing parameters on marageing steels [22], the modelling of strain induced martensitic transformation [23], and the reduction in steel varieties [28], to name but a few. There has even been an assessment of procedures needed to design networks which are well-assessed in their performance [24]. Given this plethora of literature, only specific points of relevance are introduced here.

With neural networks, the input data $ x_j$ are multiplied by weights, but the sum of all these products forms the argument of a flexible mathematical function (known as the transfer function), here a hyperbolic tangent. The output $ y$ is therefore a non-linear function of $ x_j$. The exact shape of the hyperbolic tangent can be varied by altering the weights. Further degrees of non-linearity can be introduced by combining several of these hyperbolic tangents, so that the network is able to model highly non-linear relationships. The nature of the transfer functions and the weights define a reproducible mathematical function which represents the empirical data.

The network just described is essentially a non-linear regression method which, because of its flexibility, is able to capture complicated data, whilst at the same time avoiding overfitting. There are a number of interesting outputs other than the coefficients which help recognise the significance of each input. First, there is the noise in the output, associated with the fact the input set is unlikely to be comprehensive - i.e., a different result is obtained from identical experiments. Secondly, there is the uncertainty of modelling because many mathematical functions may be able to adequately represent known data but which behave differently when extrapolated. A knowledge of this uncertainty helps make the method less risky in extrapolation. This uncertainty can be expected to be large in regions of the input domain where data are sparse or exceptionally noisy.

The Variables

Published [25] fatigue crack growth data for tests done in ordinary air, at room temperature, were digitised, covering steels with chemical compositions in the range presented in Table 1. Traces element concentrations (Ti, Al, V, S, P) together with the details of heat treatment can be found in the original compilation [25]. The properties of a steel depend on the composition and heat treatment, but fatigue crack propagation should depend to a large extent on macroscopic mechanical properties. It was deliberately decided to focus on easily measured properties obtained from a tensile test, rather than use inputs such as the threshold stress intensity which would defeat the purpose of modelling since a fatigue test would be required before a prediction could be made. The dimensions of the test specimens and the test conditions are also important in this respect and were included in the analysis. The advantage of this approach also is that a large quantity of data are available with each of the input variables listed in Table 1. Data for both axial mode I and an in-plane bending mode II were incorporated; mode III data were not available.

The plots in Fig. 1 illustrate the distribution of data, but clearly cannot represent multidimensional dependencies. However, the neural network method used here is based on a Bayesian framework [15,13] so that the predictions are associated with a modelling uncertainty whose magnitude depends on the position in the input domain where a calculation is done. . As pointed out previously, the details of the neural network and Bayesian framework used have been fully described elsewhere so only the essential points are included in this paper.

Training the Model

The data were randomly and equally divided into the training and testing sets, and normalised [11]. One hundred networks were trained, with hidden units ranging from one to twenty and five seeds in each case. This is in order to select a committee of models which gives the best generalisation on unseen data [29,14,13,11]. The performance of the optimum committee accompanies by $ \pm 1 \sigma$ modelling uncertainties is illustrated in Fig. 2. Of the total of 12807 data, only 158 can be classified as mild outliers which are more than 3$ \sigma$ from the measured values. The noise in the output of the committee model was found to be $ \sigma= \pm 4\%$, which is a constant additional error to the modelling uncertainties plotted in subsequent graphs. The network perceived significances, which indicate the ability of an input to explain the variation in the output (akin a partial correlation coefficient) are shown in Fig. 3. The elongation, ultimate tensile strength and proof stress are significant in influencing $ da/dN$ but it is natural that the stress intensity range $ \Delta K$ should have the greatest effect. Although it is expected in a valid test that specimen size should not influence $ da/dN$ [30], it is likely that true plane strain conditions do not exist in all the cases studied, and hence a specimen size effect is perceived in Fig. 3. Such behaviour has been reported previously, with the crack growth rate increasing as plane-strain conditions are approached [31].

One way of assessing a model is by making predictions, in this case on a bearing steel of relevance in our other research. The steel of interest is variously known as SUJ2, AISI 52100 and En31 in different countries and has the approximate composition 1C, 0.3-1.1Mn, 1.2-1.4Cr, 0.2-0.4Si wt%. The inputs required were obtained from [32]: 5% elongation, 2030 MPa 0.2% proof stress, 2240 MPa tensile strength, loading mode 2, specimen length 80 mm, specimen thickness 2 mm, pre-crack size 3 mm, frequency 2 Hz and stress ratio 0.

Fig. 4 shows the outcome, with the model not only capturing the trend in the variation of $ da/dN$ versus $ \Delta K$ over several orders of magnitude, and both for the threshold and Paris regions of the curve, but giving also a reasonable absolute prediction accuracy.

Although all of the data used to create the model were from experiments on steels [25], the inputs include only mechanical and test parameters. It was imagined that the model should therefore apply without modification to other alloys.

Ni, Ti and Al Alloys

Calculations for three nickel-base superalloys Udimet 700, Inconel 718 and Waspaloy; their detailed compositions can be found in [36,37,34,35,33]. Fig. 5 compares the model and the experimental data using the inputs listed in Table 2. The calculations are represented with the uncertainty range and the reported measurements [36,37,34,35,33] as points. The results are fascinating since the model correctly estimates the Paris slopes, although it marginally overestimates the fatigue behaviour (we have checked that this overestimation is not explained by modulus variations between the different materials). A similar level of agreement was found for titanium Ti-6Al-4V, 7075 aluminium alloy were made and compared against published measurements [38,39], Fig. 6. The model nicely captured the slope for both the titanium and aluminium alloys, and it again slightly overestimates the fatigue crack growth rates.

In order to further test the model a colleague from industry supplied input data (last two columns, Table 2) without revealing the alloy type for the purpose of making blind predictions, for which the crack growth rates would be revealed after the calculations are made. Fig. 7 shows calculations, and the subsequent experimental data on the same Ti6Al4V alloy with two different heat treatments. The agreement obtained is good.

Conclusions

  1. It has been possible to design a neural network model for fatigue crack growth in steels, which relies on inputs that consist only of properties that can be obtained from a simple tensile test, and using information about specimen geometry and testing parameters.
  2. Given the nature of the inputs, it has been demonstrated that although the model is based entirely on data from steels, it can be applied without modification to nickel, titanium and aluminium alloys.
  3. Given recent work where a similar approach has been used in modelling the hot-tensile strength [40] and stretch flangeability [41], it becomes evident that the neural network method has enormous potential for creating models for complex mechanical properties on the basis of simple experiments, such as the data obtained during tensile testing.

The computer program associated with this work can be downloaded freely from:

Acknowledgements

RCD would like to thank the European Commission, Marie Curie Early Stage Research Training Programme.

Bibliography

1
P. C. Paris, M. P. Gomez, and W. E. Anderson.
A rational analytic theory of fatigue life.
The Trend in Engineering, 13:9-14, 1961.
2
P. C. Paris and F. Erdogan.
A critical analysis of crack propagation laws.
J. Basic Eng.(Trans. ASME), 85:528-534, 1963.
3
P. C. Paris.
The fracture mechanics approach to fatigue.
Proc. 10th Sagamore Conf, pages 107-132, 1965.
4
R. O. Ritchie.
Near threshold fatigue-crack propagation in steels.
International Metals Reviews, 4:205-230, 1979.
5
L. N. McCartney and P. M. Cooper.
A new method of analysing fatigue crack propagation data.
Engineering Fracture Mechanics, 9:273-290, 1974.
6
K. H. Schwalbe.
Comparison of several fatigue crack propagation laws with experimental results.
Engineering Fracture Mechanics, 6:325-341, 1974.
7
W. Elber.
The significance of fatigue crack closure.
ASTM STP, 486:230-242, 1971.
8
T. V. Duggan.
A theory for fatigue crack propagation.
Engineering Fracture Mechanics, 9:735-747, 1977.
9
D. V. Ramsamooj and T. A. Shugar.
Model prediction of fatigue crack propagation in metal alloys in laboratory air.
International Journal of Fatigue, 23:S287-S300, 2001.
10
S. Shademan, A. B. O. Soboyejo, J. F. Knott, and W. O. Soboyejo.
Physically based model for the prediction of long fatigue crack growth in Ti-6Al-4V.
Materials Science and Engineering A, 315:1-10, 2001.
11
H. K. D. H. Bhadeshia.
Neural networks in materials science.
ISIJ International, 39:966-979, 1999.
12
M. D. Mathew, D. W. Kim, and W. S. Ryu.
A neural network model to predict low cycle fatigue life of nitrogen-alloyed 316l stainless steel.
Materials Science and Engineering A, 474:247-253, 2008.
13
D. J. C. MacKay.
Practical bayesian framework of backpropagation networks.
Neural Computation, 4:448-472, 1992.
14
D. J. C. MacKay.
Bayesian interpolation.
Neural Computation, 4:415-447, 1992.
15
D. J. C. MacKay.
Information Theory, Inference, and Learning Algorithms.
Cambridge University Press, 2003.
16
H. K. D. H. Bhadeshia.
Neural networks and information in materials science.
Statistical Analysis and Data Mining, 1:296-305, 2009.
17
T. Goswami.
Prediction of low cycle fatigue lives of low alloy steels.
ISIJ International, 36:354-360, 1996.
18
S. B. Singh and H. K. D. H. Bhadeshia.
Estimation of bainite plate-thickness in low-alloy steels.
Materials Science and Engineering A, A245:72-79, 1998.
19
J. M. Vitek, Y. S. Iskander, and E. M. Oblow.
Improved ferrite number prediction in stainless steel arc welds using artificial neural networks.
Welding Journal, Research Supplement, 79:33s-50s, 2000.
20
J. Tenner, D. A. Linken, P. F. Morris, and T. J. Bailey.
Prediction of mechanical properties in steel heat treatment process using neural networks.
Ironmaking and Steelmaking, 28:15-22, 2001.
21
D. Dunne, H. Tsuei, and Z. Sterjovski.
Artificial neural networks for modelling of the impact toughness of steel.
ISIJ International, 44:1599-1607, 2004.
22
Z. Guo and W. Sha.
Modelling the correlation between processing parameters and properties of maraging steels using artificial neural network.
Computational Materials Science, 29:12-28, 2004.
23
M. Mukherjee, S. B. Singh, and O. N. Mohanty.
Neural network analysis of strain induced transformation behaviour of retained austenite in TRIP-aided steels.
Materials Science and Engineering A, 434A:237-245, 2006.
24
H. K. D. H. Bhadeshia, R. C. Dimitriu, S. Forsik, J. H. Pak, and J. H. Ryu.
On the performance of neural networks in materials science.
Materials Science and Technology, 25:504-510, 2009.
25
M. Jono, Y. Iono, A. Ohta, S. Kawai, H. Kobayashi, K. Komai, T. Sakai, K. Hirakawa, and K. Mori.
Data book on fatigue crack growth rates of metalic materials, vol. 1 and vol. 2.
Technical report, The Society of Materials Science, Japan, Kyoto, Japan, 1983.
26
J.-H. Pak, J.-H. Jang, H. K. D. H. Bhadeshia, and L. Karlsson.
Optimisation of neural network for Charpy toughness of steel welds.
Materials and Manufacturing Processes, 24:16-21, 2009.
27
J. H. Ryu and H. K. D. H. Bhadeshia.
Contribution of microalloying to the strength of hot-rolled steels.
Materials and Manufacturing Processes, 24:1-7, 2009.
28
M. S. Joo, J. H. Ryu, and H. K. D. H. Bhadeshia.
Domains of steels with identical properties.
Materials and Manufacturing Processes, 24:53-58, 2009.
29
D. J. C. MacKay.
Bayesian non-linear modelling for the energy prediction competition.
ASHRAE Transactions, 100:1053-1062, 1994.
30
J. R. Griffiths and C. E. Richards.
Fatigue testing.
Mater. Sci. Eng R, 11:305-315, 1973.
31
D. Broek and J. Schijve.
Fatigue crack growth; effect of sheet thickness.
Aircraft Engineering, 38:31-33, 1966.
32
A. Otsuka, Y. Fujii, and K. Maeda.
A new testing method to obtain mode 2 fatigue crack growth characteristics of hard materials.
Fatigue Fract Engng Mater Struct, 27:203-212, 2004.
33
M. A. Hicks and J. E. King.
Temperature effects on fatigue tresholds and structure sensitive crack growth in a nickel-base superalloy.
Int. J Fatigue, 5:67-74, 1983.
34
R. L. Tobler.
Low temperature effects on the fracture behaviour of a nickel base superalloy.
Cryogenics, 1:669-674, 1976.
35
L. A. James and W. J. Mills.
Effect of heat treatment and heat to heat variations in the fatigue crack growth response of alloy 718.
Engineering Fracture Mechanics, 22(5):797-817, 1985.
36
J. Telesman and L. J. Ghosn.
The unusual near-treshold fatigue crack growth behaviour of a single crystal superalloy and the resolved shear stress as the crack driving force.
Engineering Fracture Mechanics, 34(5/6):1183-1196, 1989.
37
J. C. Healy, L. Grabowski, and C. J. Beevers.
Short fatigue crack growth in a nickel base superalloy at room and elevated temperature.
Int J. Fatigue, 2:1183-1196, 1991.
38
S. S. Tschegg.
Fatigue crack growth and thresholds at ultrasonic frequencies.
Int J. Fatigue, 28:1456-1464, 2006.
39
T. L. MacKay.
Fatigue crack propagation rate at low $ {\Delta}$K of two aluminium sheet alloys, 2024-T3 and 7075-T6.
Engineering Fracture Mechanics, 11:753-761, 1979.
40
R. Dimitriu and H. K. D. H. Bhadeshia.
Hot-strength of creep-resistant ferritic steels and relationship to creep-rupture data.
Materials Science and Technology, 23:1127-1131, 2007.
41
S. Chatterjee and H. K. D. H. Bhadeshia.
Stretch-flangeability of strong multiphase steels.
Materials Science and Technology, 23:606-609, 2007.

.


Table 1: Chemical composition range (wt%) of the steels studied. The lower half of the table shows the variables actually included in the analysis.
Element Range      Element Range
Carbon 0.1-0.8   Copper 0-0.2
Chromium 0-5   Manganese 0-2
Molybdenum 0-2   Nickel 0-2
Silicon 0-2      
Variable Range      Variable Range
Elongation / % 0.2 -61.8   0.2% Proof stress / MPa 122-1735
Tensile strength / MPa 270-2206   Specimen length / mm 13-260
Specimen thickness / mm 1.2-134   Pre-crack length / mm 1-52
Stress ratio -1-1   Frequency / Hz 1-150
$ \Delta K$/ MPam$ ^{1/2}$ 2.5-142   $ \frac{da}{dN}$/ mm cycle$ ^{-1}$ 9.82$ \times$10$ ^{-10}$-4.86$ \times$10$ ^{-1}$
       


Table 2: The inputs for the predictions in Figs 5, 6, 7 covering nickel, titanium and aluminium alloys.
Variable Figure number
  5a 5b 5c 5d 5e 5f 6a 6b 7a 7b
Elongation / % 5 15 20 20 27 33 14 8 20 14
0.2% Proof stress / MPa 1020 1172 1113 1113 1076 921 930 524 1172 940
Tensile strength / MPa 1520 1404 1373 1373 1441 1351 970 464 1440 998
Specimen length / mm 72.5 63.5 50.8 31.8 62.5 5 155 155 7 7
Specimen thickness / mm 12.5 25.4 12.7 8.89 25 3 40 40 7 7
Pre-crack length / mm 12.5 18.3 6.4 5.3 17.5 0.4 9 9 0.5 0.5
Stress ratio 0.1 0.1 0.05 0.05 0.5 0.5 -1 0.5 0.1 0.5
Frequency / Hz 40 20 0.667 0.667 20 100 20 20 0.25 100
                   

Figure 1: Distribution of data used to create the model.
\includegraphics[width=0.32\textwidth]{elv.eps}\includegraphics[width=0.32\textwidth]{tens.eps}\includegraphics[width=0.32\textwidth]{profstre.eps}\includegraphics[width=0.32\textwidth]{speclengt.eps}\includegraphics[width=0.32\textwidth]{specwidt.eps}\includegraphics[width=0.32\textwidth]{specpre.eps}\includegraphics[width=0.32\textwidth]{stresrati.eps}\includegraphics[width=0.32\textwidth]{freque1.eps}\includegraphics[width=0.32\textwidth]{logdkda.eps}
Figure 2: Performance of the committee of models on the entire dataset of 12807 experiments.
\includegraphics[width=0.75\textwidth]{pvmcomch2.eps}
Figure 3: Perceived significance of the inputs in the committee model. Both the mean significance and the upper and lower limits from the members of the committee are shown.
\includegraphics[width=0.95\textwidth]{sig22.eps}
Figure 4: Calculations for a bearing steel. The points represent experimental data from [32], whereas the uncertainty range illustrated is calculated.
\includegraphics[width=10cm]{pred111.eps}
Figure 5: Predictions represented by the uncertainty ra 4nge, and experimental data presented as points, for nickel based superalloys. (a) Udimet 700, data from [33]. (b) Inconel 718 with data dues to [34]. (c,d) Inconel 718, data from [35]. (e) Waspaloy, data from [36]. (f) Waspaloy, data from [37].
[a]\includegraphics[width=0.40\textwidth]{100.eps}[b]\includegraphics[width=0.40\textwidth]{101.eps}[c]\includegraphics[width=0.40\textwidth]{102.eps}[d]\includegraphics[width=0.42\textwidth]{103.eps}[e]\includegraphics[width=0.40\textwidth]{105.eps}[f]\includegraphics[width=0.40\textwidth]{106.eps}
Figure 6: Calculations (uncertainty ranges) for titanium and aluminium alloys compared with measurements (points) due to [38,39].
[a]\includegraphics[width=0.42\textwidth]{TiAlV.eps}[b]\includegraphics[width=0.42\textwidth]{7075.eps}
Figure 7: Blind predictions for Ti 6/4 forging material.
[a]\includegraphics[width=0.42\textwidth]{bt11.eps}[b]\includegraphics[width=0.42\textwidth]{bt22.eps}


Pipeline texture Mathematical Models Bake hardening Nuclear 301L stainless
Residual stress TRIP 301L stainless Hot-strength Intervention
δ-TRIP Metallography Bearings Topology Tiny bainite

PT Group Home Materials Algorithms