Grain Growth: Zener Pinning of Grain Boundaries by Oxide Particles

Shinichi Terahsima and H. K. D. H. Bhadeshia

Recrystallisation and grain growth involve the movement of grain boundaries. The motion will be inhibited by second phase particles. The drag on the boundary due to an array of insoluble, incoherent spherical particles is because the grain boundary area decreases when a boundary intersects the particle. Therefore, to move away from the particle requires the creation of new surface. The net drag force on a boundary of energy $\gamma$per unit area due to a particle of radius $r$is given by (Fig.  1)

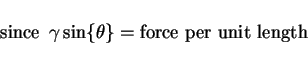\begin{displaymath} \hbox{since~~}\gamma \sin\{\theta\} = \hbox{force per unit length}\end{displaymath} (1)
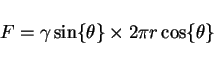\begin{displaymath}F= \gamma\sin\{\theta\} \times 2\pi r \cos\{\theta\}\end{displaymath} (2)
\begin{displaymath}\hbox{so that at~~}\theta =45^\circ \end{displaymath} (3)
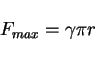\begin{displaymath}F_{max} = \gamma\pi r \end{displaymath} (4)
Figure 1:(a) The particles located within a distance $r$of the grain boundary plane can interact with the boundary. (b) The forces at the junction between the boundary and the particle. Think of the particle as a sphere which is intersecting a planar surface. The perimeter defining the intersection is $2\pi r \cos\{\theta\}$.
(a) \includegraphics[width=5.5cm]{zener1.eps}(b) \includegraphics[width=14.5cm]{zener2.eps}

Suppose now that there is a random array of particles, volume fraction

$f$with $N$particles per unit volume. Note that
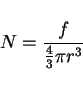\begin{displaymath}N = {{f}\over{{4\over 3}\pi r^3}}\end{displaymath} (5)

Only those particles within a distance $\pm r$can intersect a plane. The number of particles intersected by a plane of area $1\,{\rm m^2}$will therefore be

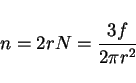\begin{displaymath}n = 2rN = {{3f}\over{2\pi r^2}}\end{displaymath} (6)

The drag pressure $P$is then often expressed as


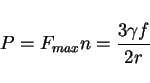\begin{displaymath}P= F_{max} n = {{3 \gamma f}\over{2r}} \end{displaymath} (7)

This may be a significant pressure if the particles are fine. Anisotropic particles may have a larger effect if they present a greater surface area for interaction with the boundary.

A grain of radius $r$has a volume ${{4}\over{3}}\pi r^3$and surface area $4\pi r^2$. The grain boundary energy associated with this grain is $2\pi r^2 \gamma$where $\gamma$is the boundary energy per unit area and we have taken into account that the grain boundary is shared between two grains. If follows that:

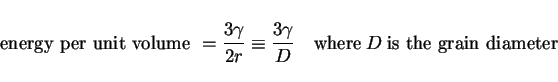\begin{displaymath}\hbox{energy per unit volume } = {{3\gamma}\over{2r}} \equiv ... ...gamma}\over{D}}\quad\hbox{where}~D~\hbox{is the grain diameter}\end{displaymath} (8)

It is this which drives the growth of grains with an equivalent pressure of about 0.1 MPa for typical values of $\gamma=0.3\,{\rm J\,m^{-2}}$and $D=10\,{\rm\mu m}$. This is not very large so the grains can readily be pinned by particles (Zener drag).

An Example

The micrographs below are from a steel sample of chemical composition Fe-0.06C-0.3Si-1.02Mn-0.2Cu-2.43Ni-0.2Cr-0.46Mo wt%, containing a variety of oxygen concentrations. The oxygen is in the form of fine oxide particles. The sample was metallographically polished and then heated to 1200°C to thermally etch the austenite grain boundaries. The oxide particles serve to prevent the growth of austenite grains during this heat-treatment, via Zener pinning. It is not surprising that the final austenite grain size decreases as the oxygen concentration increases.

The term ppmw stands for parts per million by weight.

10
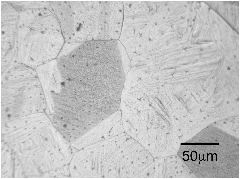10 ppmw oxygen		 110
110 ppmw oxygen		 140
140 ppmw oxygen
270
270 ppmw oxygen		 350
350 ppmw oxygen		 560
560 ppmw oxygen

Related Articles