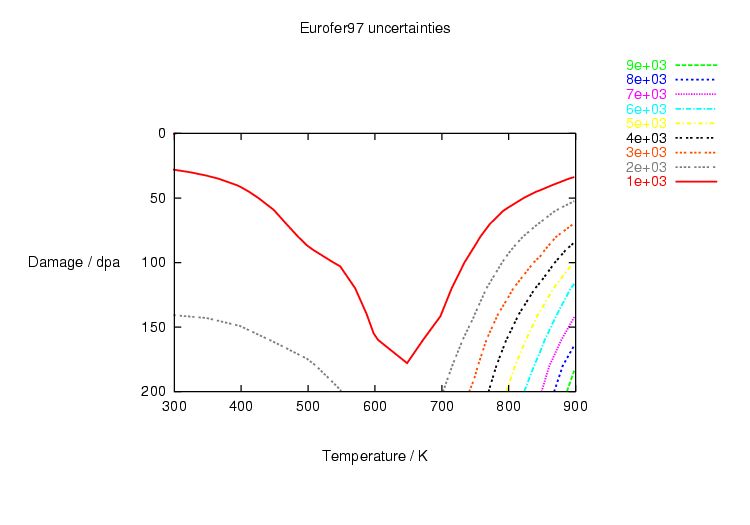
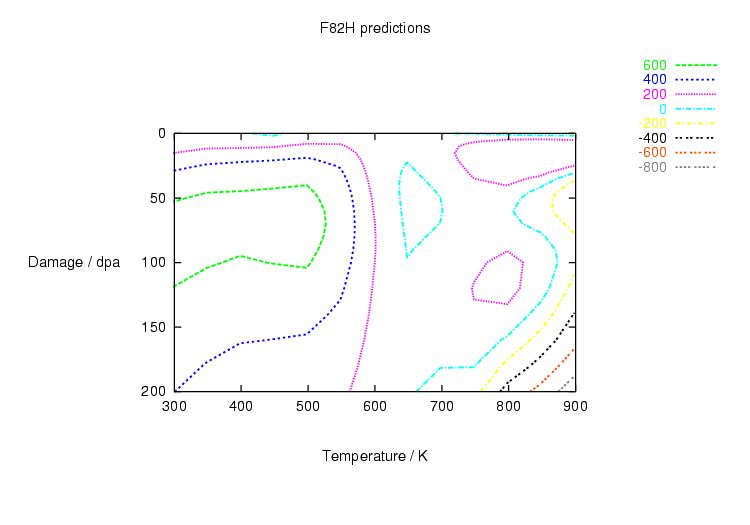
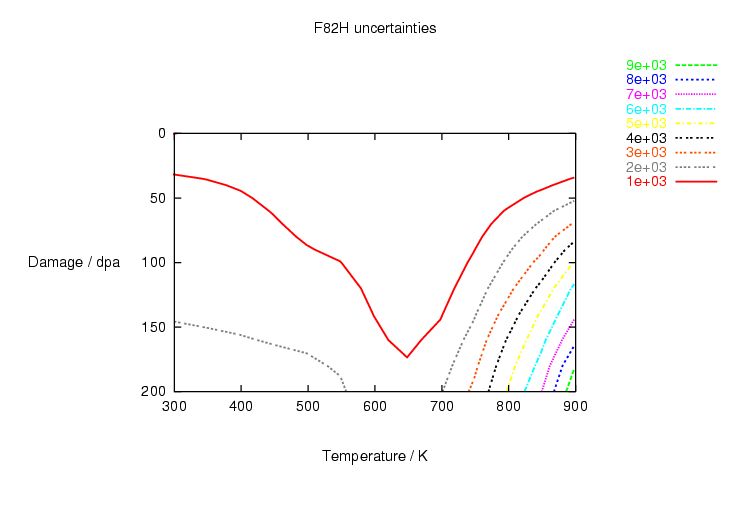
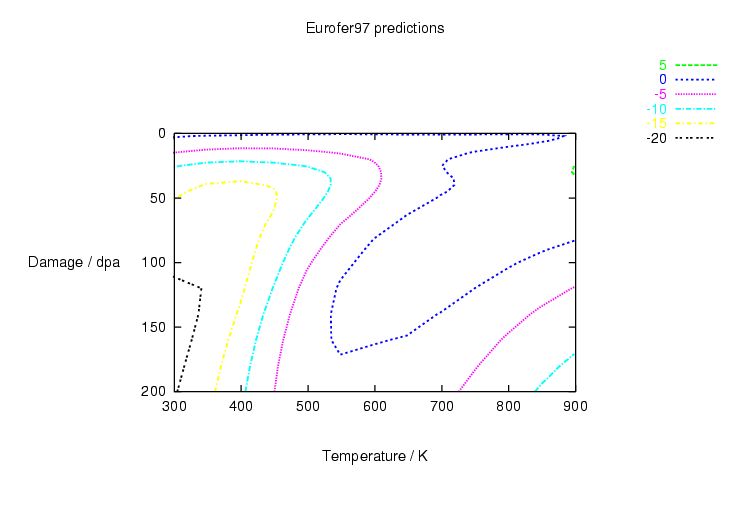
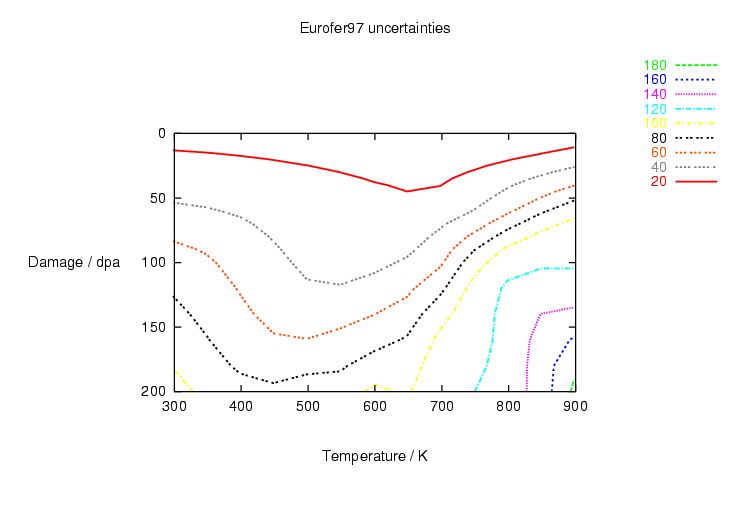
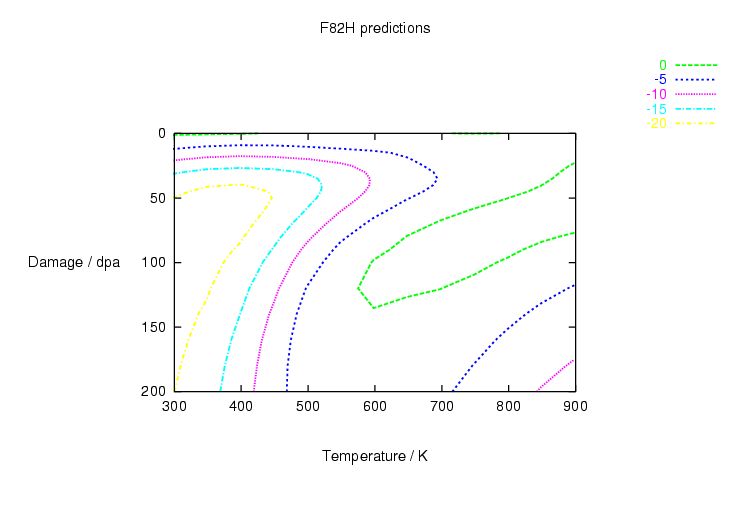
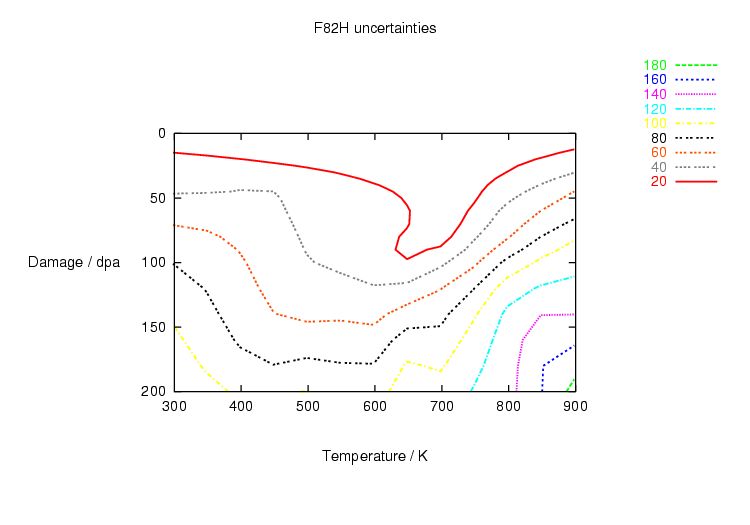
Table 1.1:
Operating conditions for the first-wall components
of ITER and a DEMO-like reactor. As ITER will be an experimental reactor,
the projected number of cycles will be very much higher than any commercial
power plant reactor (Bolt et al., 2002). PFM = Plasma facing material,
SS = stainless steel, RAFM = reduced activation ferritic/martensitic steel, dpa = displacements per atom, appm = atomic parts per million. MW yr = megawatt years - 1 MW yr ≈31.5 TJ.
| |
ITER |
DEMO-like reactor |
| Component replacements |
None |
5 year cycle |
| |
|
|
| Average neutron fluence (MW yr m-2) |
0.3 |
10 |
| Displacement damage (dpa) |
3 (SS) |
120 (RAFM) |
| Helium production (appm) |
30 |
1200 |
| |
|
|
| Normal operation |
|
|
| Number of cycles |
30000 |
<1000 |
| Peak particle flux (1023 m-2 s-1) |
0.01 |
0.02 |
| Surface heat flux (MW m-2) |
<0.5 |
<1 |
| PFM operating temperature (°C) |
Be: 200 - 300 |
W: 550 - 700 |
|
|
Table 1.2:
Functions and requirements of a fusion
power-plant blanket structure. Tritium breeding occurs through the use of coatings such as lithium, which produce tritium under neutron bombardment (Smith et al., 1994).
| Primary functions of the blanket |
| - Convert energy into sensible heat |
| - Breed tritium for the fuel cycle |
| |
| Primary requirements of the blanket |
| - Adequate tritium production |
| - Acceptable tritium recovery |
| - Efficient heat recovery |
| - Acceptable reliability and operating lifetime |
| - Ease of assembly, maintenance, and repair |
| - Acceptable post-irradiation environmental impact |
| - Acceptable economics |
|
|



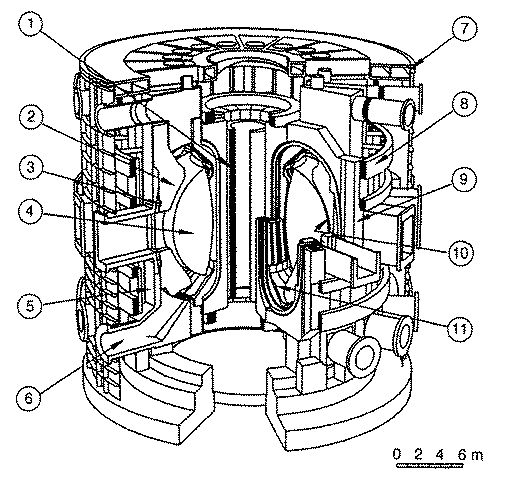
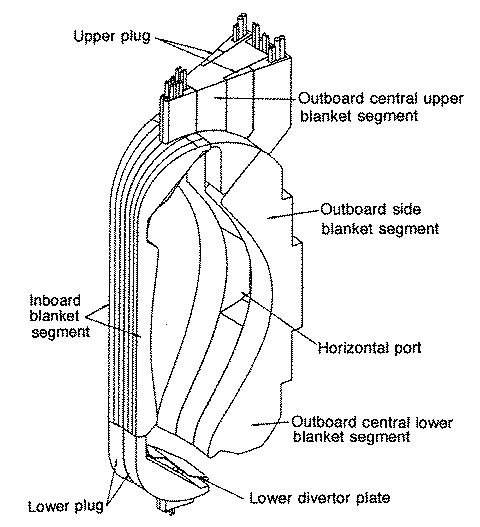
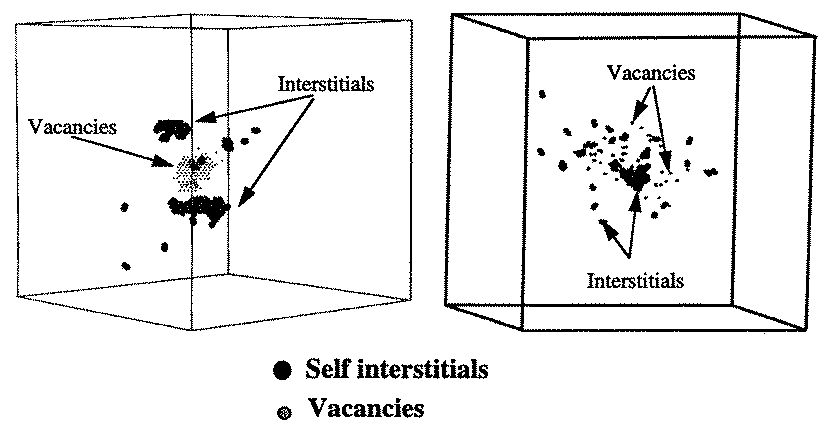
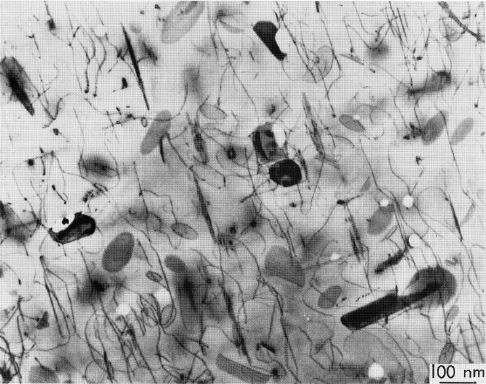
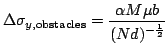
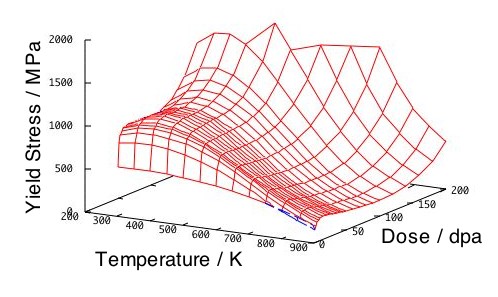 (b)
(b)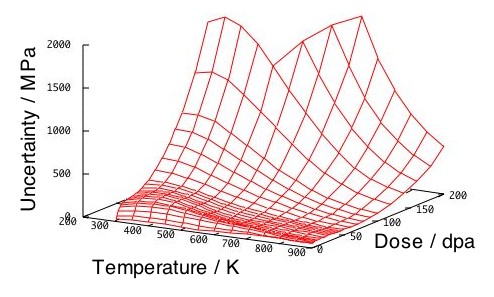
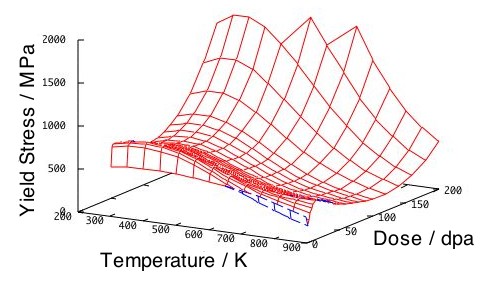 (d)
(d)