Genetic algorithm questions

Question 1

Table 1 shows a population of strings. Assuming that the string represents a binary encoding of a number n, and that the fitness function is given by 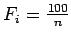$F_{i}=\frac{100}{n}$ , fill in the rest of the table using a suitable procedure such as the roulette wheel algorithm to generate a mating pool. Having done this, complete Table 2 by randomly selecting mates and single crossover sites to generate a new population. Calculate Fi for each member of the new population. Is this an improvement? (E.g has the average population fitness improved? How do the best-performing members compare?)

(20 minutes, 10 marks)


Table 1: Table for question 1.
String no. String n Fi $\frac{F_{i}}{\Sigma{}F_{i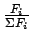}}$ No. surviving Mating pool
1 10111 23 4.35      
2 00111          
3 01001          
4 01010          


Table 2: Table for question 1.
Mating pool Mate Crossover site New population n New Fi
           
           
           
           

Question 2

A Bayesian neural network has been trained for the yield stress σy of stainless steel. The inputs to the neural network are listed in Table 3.

  1. Write down a suitable chromosome for the optimisation of this model.
  2. Assume a target yield stress σy,target is desired, with low uncertainty. Write down a suitable fitness function Fi.
  3. Draw up a flowchart showing the steps a genetic algorithm optimisation would take for this network model.

Remember to include some way of preventing non-physical values, and a suitable termination condition.

(20 minutes, 10 marks)


Table 3: Inputs to the neural network for question 2.
Input Definition
Cr Chromium (wt %)
Ni Nickel (wt %)
Mo Molybdenum (wt %)
Mn Manganese (wt %)
Si Silicon (wt %)
Nb Niobium (wt %)
Ti Titanium (wt %)
V Vanadium (wt %)
Cu Copper (wt %)
N Nitrogen (wt %)
C Carbon (wt %)
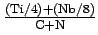Ratio Ti and Nb stabilisation ratio $\frac{(\mathrm{Ti}/4)+(\mathrm{Nb}/8)}{\mathrm{C}+\mathrm{N}}$
Theat Heat treatment temperature (K)
theat Heat treatment time (hr)
ln(theat) Natural log of theat
Ttest Tensile test temperature (K)

Answers

Model answers and a marks scheme are available here.

To return the the Genetic Algorithms page click here.

Acknowledgements

The creation of this document was supported by the Higher Education Funding Council for England, via the U.K. Centre for Materials Education.


June 5th 2006


Superalloys Titanium Bainite Martensite Widmanstätten ferrite
Cast iron Welding Allotriomorphic ferrite Movies Slides
Neural Networks Creep Mechanicallly Alloyed Theses

PT Group Home Materials Algorithms Any Valid CSS!