Heat Transfer Experiments

Hala Salman Hasan, Mathew Peet and H. K. D. H. Bhadeshia

We use the example of casting a molten metal into a mould to illustrate the transfer of heat across a gap (an interface), given by:

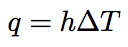
where q is the heat flux, h is the thermal conductance of the interface and ΔT the temperature difference between the source and the sink. Values of the heat transfer coefficient vary widely: 10→10² W m^-2 K^-1 for large air gap; 10³→10⁴ for normal castings with gravity contact; 10⁵→10⁶ for excellent contact as in pressure casting. The temperature profile obtained depends on the a comparison of the heat conductance of the interface with that of the whole casting. The thermal conductance of a casting is written K/L where where K is the thermal conductivity of a casting of length L in the direction of heat flow. The ratio of the thermal conductance of the interface (h) to that of the casting, termed the Biot number:

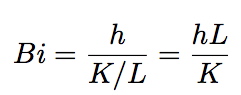
For small Bi the thermal resistance of the interface dominates that of the casting, which therefore remains at approximately a constant temperature. This is called Newtonian cooling.

Heat Transfer During Quenching

The mathematical simulation of the time and temperature during the quenching of hot metal into a liquid depends on the accuracy of data such as the heat-transfer coefficient h. Heat transfer during quenching into liquid is complicated when the quench medium forms a gas when heated to high temperatures.

The quenching process is usually categorised into a number of stages.

• Stage 1. Vapour blanket.
  • The cooling rate in this stage is slow because the vapour envelope acts as an insulator, with cooling occurring primarily by radiation through the vapour film. Depends upon surface roughness, quenchant temperature, quenchant type, oxidation.
• Stage 2. Nucleate boiling.
  • In this stage, the vapour envelope collapses, with rapid heat removal as the liquid comes into contact with the metal surface and becomes vapourised.
• Stage 3. Liquid cooling.
  • This begins when the temperature of the metal surface is reduced below the boiling point of the quenchant. Boiling stops and cooling occurs by conduction and convection into the quenchant. The convective flow may be turbulent or lamellar.

The images that follow show a sample designed to measure the heat transfer coefficient during the quenching steel into water. The sample is small to ensure a small Biot number. It is much smaller than a similar sample for aluminium due to the lower thermal conductivity of steel.

An accurate knowledge of the heat transfer coefficient should lead to the better estimation of temperature gradients and cooling rates during quenching.

Heat transfer sample	Heat transfer sample
Heat transfer sample, showing the thermocouple	Heat transfer sample
Heat transfer sample, showing the thermocouple	Movie of probe being quenched

Ph.D. Thesis and Publications

• Evaluation of heat transfer coefficient during quenching of steels, by Hala Salman Hasan
• Heat and mass transfer
• Thermal conductivity
• Heat transfer coefficient and latent heat

Computer programs and data:

Quench Distortion

With some steels, it is necessary to rapidly cool a component in order to achieve martensitic transformation and the desired strength and hardness. Rapid cooling is associated with large temperature gradients, which in turn lead to the development of residual stress. The component will distort when the stresses are not uniform. The heterogeneous distribution of the stresses which lead to distortion can be induced either by a nonuniform shape or nonuniform cooling.

The movies below are from experiments conducted by Professor M. Narazaki (Utsunomiya University, Japan) and reproduced with the permission of Dr K. Arimoto for teaching purposes.

There are two movies showing the quenching of a shaft with a keyway parallel to its length. The first movies shows quenching in water and the second in a polymer solution. The latter is associated with more uniform cooling and less distortion. The movies are in MPG format (2 Mb).

• Water quench.
• Polymer solution quench.

More photographs of the probe experiments

Mathew Peet
Mathew again
Hala Salman Hasan, pretending to work	Hala, not pretending