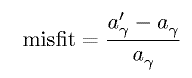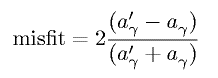Rafting in Nickel Based Superalloys

H. K. D. H. Bhadeshia

In nickel based superalloys the γ phase forms the matrix in which the γ' precipitates. Since both the phases have a cubic lattice with similar lattice parameters, the γ' precipitates in a cube-cube orientation relationship with the γ. This means that its cell edges are exactly parallel to corresponding edges of the γ phase. Because their lattice parameters are similar, small particles of γ' are coherent with the γ.

In high volume fraction γ' alloys the microstructure following heat-treatment consists of cuboids of precipitate separated by channels of γ matrix. γ' coarsening is driven by the minimisation of the interfacial energy per unit volume in the absence of an applied stress. The coarsened microstructure remains essentially the same (albeit with a bigger length scale), i.e. with channels of γ separating the more or less cuboidal precipitates of γ'.

Transmission electron micrograph showing square sections of cuboidal γ' particles in a γ matrix, in a single-crystal alloy SRR99. The plane of the image is parallel to {100} plane. Notice the channels of γ between the precipitates. The images can be enlarged.	Transmission electron micrograph showing triangular sections of cuboidal γ' particles in a γ matrix, in the same alloy. The plane of the image is parallel to {111} plane. These images have kindly been provided by Bernard Fedelich: Computational Materials Science 16 (1999) 248-258.

However, the development of microstructure during coarsening under the influence of an applied stress is quite different. The γ' particles coalesce to form layers, known as rafts.

Rafting in a single-crystal superalloy, under the influence of a tensile stress applied at elevated temperature. Image provided by A. C. Yeh.	Rafting in perspective, as layers in three dimensions. Image provided by A. C. Yeh.

It is necessary to define the crystallographic misfit between the γ and γ' in order to describe the process of rafting. There are two ways in which this is normally done (either way is acceptable):

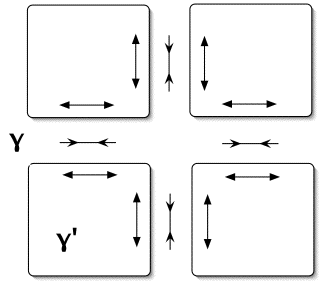
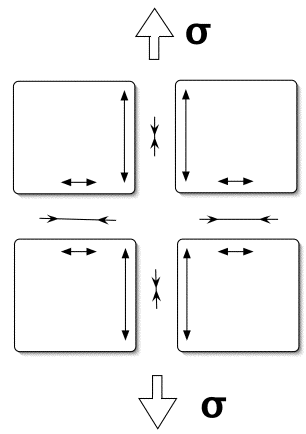
A negative misfit means that the γ' has a smaller lattice parameter than that of γ. The latter will therefore be in compression in the vicinity of the interface with γ', and there will be compensating tensile stresses in the γ' as illustrated in the figure below. The application of a uniaxial tensile stress exaggerates any tensile stress in the vertical direction and reduces those in the horizontal orientation. Similarly, the applied tensile stress reduces the compressive stress in the vertical γ channels and via the Poisson effect, increases those in the horizontal channels.

The greater stresses in the horizontal γ channels lead to enhanced creep; the resulting dislocations enter the γ/γ' interface and accommodate the misfit in the horizontal interfaces. Rafting then tends to eliminate the elastically strained vertical channels, leading to a net reduction in free energy.

Illustration of the major components of the coherency stresses in the vicinity of the γ/γ' interfaces for a case where the misfit is negative. Adapted from Kamaraj.	The modification of the coherency stresses as a consequence of an externally applied tensile stress σ in the vertical direction.

The orientation of the rafts clearly must be a function of that of the applied stress. The rate of rafting depends on the magnitude of the stress and the magnitude of the lattice misfit between the γ and γ' crystals. It must also have an independent dependence on the chemical composition of the alloy since the process involves the transfer of matter via multicomponent diffusion.

A full discussion of rafting should account for the ratio of the elastic modulus of the precipitate to that of the matrix; the orientation of rafting can change depending on whether this ratio is greater or less than unity. Rafting is predicted not to occur if the ratio is unity and the applied stress elastic.

Rafts of γ' lying normal to an applied tensile stress increase the resistance to creep when the strain is controlled by the climb of dislocations over γ' particles. This is the case at low-stresses. However, the rafts are detrimental if the dislocations are able to cut through the rafts, since a rafted state is coarse when compared with the original microstructure. The cutting occurs when the applied stress is sufficiently large.

In nickel based alloys designed for turbine blades, the fraction of γ' that precipitates from the γ matrix is typically in excess of 0.7. The changes associated with rafting cause a topological inversion in which the γ' coalesces to become the matrix with the minority γ enclosed in such a way that it appears like the included phase.

The topological change can be followed by measuring the number of phase terminations as illustrated below, where γ' terminations are represented by black dots, and by white dots for γ terminations. The ratio of the number of terminations in the γ' to γ is designated R.

The phases are said to be topologically equivalent when R=1. A value greater than unity implies a γ matrix and vice versa. The micrographs below have been reproduced with the permission of A. Epishin and U. Brückner. The full theory of inversion is described in A. Epishin, T. Link, and U. Brückner and P. D. Portella, Acta Materialia, 49 (2001) 4017.

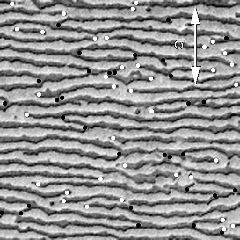
Scanning electron micrograph of SRR99, showing the undeformed microstructure. There are γ' precipitates in a γ matrix. The γ' terminations are marked with black dots.	The same sample after creep at 980°C, 200 MPa, for 85.7 hours. The microstructure is completely rafted with the number of γ terminations (white dots) and γ' terminations being identical.
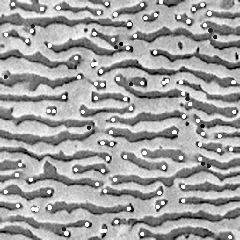
The same sample after creep at 980°C, 200 MPa, for 243 hours. The phases have topologically inverted, with many more γ terminations than γ' terminations. The γ is now in a matrix of γ'	The same sample after creep at 980°C, 200 MPa, for 243 hours, this time deeply etched to remove the γ' It appears that there is some continuity in the γ even after topological inversion.

• M. Kamaraj, Sadhana, 28 (2003) 115-128.
• T. Ohashi, Aerospace Materials, Chapter 20, Institute of Physics, London, 2001, 265-284. Editors B. Cantor, P. Grant and H. Assender.
• N. Matan, D. C. Cox, C. M. F. Rae and R. C. Reed, Acta Materialia 47 (1999) 2031-2045.
• A. Epishin, T. Link, and U. Brückner and P. D. Portella, Acta Materialia, 49 (2001) 4017-4023.

More information on nickel based superalloys.

PT Group Home

Materials Algorithms