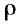Metals and Alloys

Annealing Twins

T. Sourmail, P. Opdenacker, G. Hopkin and H. K. D. H. Bhadeshia

A pair of grains is said to be twinned when the arrangement of atoms in one of the grains can be generated from the other by reflection across a common plane [Note 1]. The crystal structure of the two grains is identical, they simply are in different orientations in space.

Because twins have such a special orientation relationship, the boundaries separating the twins have a very low energy per unit area. In other words, it is possible to fit the two crystals together rather neatly. The twin-boundaries therefore tend to be flat and the twin as a whole will have a facetted appearance. In cubic close-packed metals such as copper and nickel, the major part of the twin interface is parallel to {111} planes which have the stacking sequence ..ABCABC.... The stacking sequence of the {111} planes on the other side of the twin boundary is a mirror refelction, so that the sequence across the boundary is ...ABCABACBA.... The central B layer thus represents the coherent, low-energy boundary between the twin and the matrix.

Annealing twins are formed as a consequence of growth accidents during the recrystallisation of deformed cubic-close packed metals such as alpha-brass, copper, nickel and austenitic iron [Note 2].

Annealing twins should be distinguished from mechanical twins. In the latter case, the twin orientation is generated by a large deformation of a single grain. There is a lot of strain energy associated with the formation of a mechanical twin, whose shape is determined strictly by the need to minimise strain energy. This contrasts with annealing twins where the shape is determined by the need to minimise interfacial energy. Mechanical twins tend to be lenticular, i.e., lens shaped with sharp edges, since this reduces the long range elastic strains. Annealing twins, as you will see below, are not pointed since there is no deformation associated with their formation.

Annealing twins were seen in gold as early as 1897 (Liversidge). A great deal of empirical evidence suggests that the important factors determining the frequency with which they occur are (Rath et al. 2000):

grain size;
temperature and time of annealing;
grain boundary velocity;
grain boundary energy;
twin boundary or stacking fault energy;
crystallographic texture;
degree of prior deformation;
presence of inclusions.

A large grain boundary velocity favours the formation of annealing twins because growth accidents, which are responsible for annealing twin formation, are then more frequent. Naturally, a low stacking fault energy also favours annealing twins since growth accidents are easier to tolerate. In fact, there is a simple equation which relates the twin density 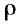$\rho$ to the grain size and a constant related to the inverse of the stacking fault energy:

$\begin{displaymath}\rho = {{b}\over{d}}\log{{d}\over{d_0}}\end{displaymath}$

where

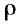is the grain size at which $\rho$ is zero.

For more details on twinning, see Worked Examples in the Geometry of Crystals, a book which is available on-line for free download.

Shows the grain structure of an austenitic stainless steel NF709, observed using light microscopy on a specimen polished and etched electrolytically using 10% oxalic acid solution in water. Many of the grains contain annealing twins. NF709 is a creep-resistant austenitic stainless steel used in the construction of highly sophisticated power generation units.

Annealing twins formed in austenite from a low-alloy steel. Austenite is unstable in such steels so it is not ordinarily possible to look at the austenite grain structure except at temperatures in excess of 900^oC. This particular sample was prepared metallographically to a 1 micron finish and then heated at 1200^oC in a vacuum containing only a trace of oxygen. The heat gives thermally grooves the surface to reveal the austenite grains, and the oxygen slightly oxides the surface to give an etching effect. The sample is then cooled to room temperature but the transformation of the austenite to ferrite does not influence the grooves or the oxide-etching, thus revealing the austenite grain structure. Notice the annealing twins. The chemical composition of the steel is Fe-0.16C-1.43Mn-0.33Si-0.56Cr-0.23Mo- 0.056V-0.064Al-0.062Ni wt%.

The transmission electron micrographs presented below are taken at 200 kV, from a thin foil sample of "302AA" austenitic stainless steel. The sample was cold-deformed by rolling and then annealed at 704 ^oC for one hour. All images show partially recrystallised microstructures. The recrystallised grains are clean (largely free from defects) whereas the deformed regions show a large concentration of defects such as dislocations and cell boundaries. There are annealing twins in the recrystallised regions.

	Shows a recrystallised grain which is relatively free of dislocations, surrounded by a deformed matrix which has a high dislocation density. The recrystallised grain contains annealing twins (parallel bands with different contrast).
	Shows recrystallised grains which which show uniform contrast because they are relatively free of dislocations, surrounded by a deformed matrix which has a high dislocation density. The recrystallised grain contains annealing twins (parallel bands with different contrast. The steps at the top left-hand corner are simply steps in annealing twin boundaries.
	Shows a beautiful picture of annealing twins. Notice how the ends of annealing twins are flat, the shape being determined by a minimisation of interfacial energy. Mechanical twins, by contrast, are lenticular (lens like) with sharply pointed ends to minimise the strain energy due to the twinning shear. Annealing twins do not cause any deformation so strain energy minimisation is not an issue. This is also the reason why there is no strain field contrast visible at the tips of the annealing twins.
	Electron back scatter image illustrating annealing twins in austenitic stainless steel (image courtesy of Arpan Das). More details.

Footnotes

[Note 1]
This definition of twin orientations in terms of reflection about a particular plane is not accurate. Other operations (such as an appropriate rotation) can also lead to twin-related grains. For more details see Worked Examples in the Geometry of Crystals, a book which is available on-line for free download.

[Note 2]
The growth-accident hypothesis indicates that annealing twins are formed and terminated by errors in the stacking of the {111} planes, which happen in a random way. See Physical Metallurgy, editors R. W. Cahn and P. Haasen, fourth edition, p. 897. Note also that the frequent assumption that the tendency for annealing twin formation correlates with a low stacking fault energy is not in itself a good assumption since there are many factors other than the fault energy which influence twin formation. Nickel, for example, has a high stacking fault energy and yet shows annealing twins.

References

A. Liversidge, J. Chem. Soc. 71 (1897) 1125.
B. B. Rath, M. A. Imam and C. S. Pande, Mater. Phys. Mech. 1 (2000) 61.

Acknowledgment

We would like to thank David Tricker, for all his help with the transmission electron microscopy.

The lady in blue doing this Flamenco dance is Yi Chen Chang, a student of Professor Jer Ren Yang, working on annealing and mechanical twins at the National Taiwan University. More photographs on https://www.phase-trans.msm.cam.ac.uk/2011/Taiwan_2011/index.html

We illustrate here the high-pitched "cry" emitted by indium when it undergoes plastic deformation by mechanical twinning. Tin exhibits a similar phenomenon.

Links

Superalloys	Titanium	Bainite	Martensite	Widmanstätten ferrite
Cast iron	Welding	Allotriomorphic ferrite	Movies	Slides
Neural Networks	Creep	Mechanicallly Alloyed	Theses	Retained Austenite

PT Group Home

Materials Algorithms