
H. K. D. H. Bhadeshia
The casual metallurgist would be wrong; there is a richness in the subject which inspires deep study. There are phenomena which are little understood, apparently incommensurate observations, some significant developments and other areas where convincing conclusions are difficult to reach. The subject seemed ready for a critical assessment; hence, this review. The structure and properties of bearing steels prior to the point of service are first assessed and described in the context of steelmaking, manufacturing and engineering requirements. This is followed by a thorough critique of the damage mechanisms that operate during service and in accelerated tests.
The Oxford English Dictionary defines a bearing ``as a part of a machine that allows one part to rotate or move in contact with another part with as little friction as possible". Additional functions include the transmission of loads and enabling the accurate location of components. A bearing may have to sustain severe static as well as cyclic loads while serving reliably in difficult environments. Steels are well-suited in this context, and in their many forms, represent the material of choice in the manufacture of bearings. There has been more than a century of work on alloys for rolling bearings; an elegant summary of the advances in steel and processing technologies that led to the contemporary state of affairs has been given by Zaretsky [1, 2]. And yet, a cursory glance at the literature reveals that the subject remains fascinating, with many unresolved issues, disparate observations and a need for radical innovations to deal with the modern requirements of large rotating components serving in somewhat unpredictable environments.
Bearings consist of rolling elements (balls, cylinders or barrel shapes) and rings which form the raceways. The manufacturing process for the rolling elements involves the high reduction-rate plastic deformation of raw, cast material, into billets with square sections. The deformation helps to break up the cast structure and to close porosity. The billets are then reduced in section by further rolling or drawing, heat-treated to a softened state and cut into lengths suitable for the manufacture of balls; the finished rolling elements are then quenched and tempered, or isothermally transformed, to the required hardness. Bearing rings can be made from seamless tube produced by hot-rolling and similarly hardened, followed by careful machining and grinding to the final dimensions and surface finish. The vast majority of rolling elements and raceways are made using steel.
This review is an exploration of the nature of bearing steels and their performance during service, based entirely on openly available published literature. The focus is on metallurgy but it has been necessary to cover aspects of engineering in order to present a coherent picture. I have attempted to cover the widest possible range of alloys but it is inevitable that the greatest attention is paid to those which are most versatile, most used and deeply researched.
It is worth emphasising at the outset that the demands made on any candidate bearing alloy go well beyond considerations of final structure and mechanical properties. The ability of the material to cope with each step in the sequence of manufacturing processes is seminal to its success or failure; a conservative list of the requirements is presented in Fig. 1. Of the very many alloys that have been investigated in the history of bearing steels, there are only two categories of steels which find application in the majority of bearings; those which are hardened throughout their sections into a martensitic or bainitic condition, and others which have soft cores but tenacious surface layers introduced using processes such as case or induction hardening. We shall see that within these categories, there is a just a handful of alloys which dominate the market for the simple reason that they best meet all of the manufacturing and engineering requirements. A great deal of the initial part of this section will focus on steels which are tempered or transformed at temperatures less than 300 ![]() C and which contain low concentrations of substitutional solutes when compared with the specialised alloys which are described later. The latter include secondary-hardening steels for bearings designed to operate at elevated temperatures or others which are designed to resist corrosion.
C and which contain low concentrations of substitutional solutes when compared with the specialised alloys which are described later. The latter include secondary-hardening steels for bearings designed to operate at elevated temperatures or others which are designed to resist corrosion.
![\includegraphics[width=0.9\textwidth]{requirements.eps}](img78.png)
|
The purpose of this section is not to give a comprehensive description of the vast variety of bearing geometries, but rather to establish the basic terminology which is used in experimental investigations. Much more detail including images of specific bearing configurations can be found elsewhere [4]. Aspects of geometry can dramatically influence the choice of material, bearing performance and its ability to bear loads. For example, the contact angle defined in Fig. 2 influences fatigue life and the temperatures developed during bearing operation [5].
Spherical balls enclosed between two concentric rings permit the rings to rotate relative to each other, whilst supporting a radial load; this is the essence of a ball bearing. Roller bearings use cylinders instead of balls and have a greater load bearing capacity because of the greater contact between the rolling element and the rings. Cylindrical roller bearings played a seminal role in the development of the continuous rolling mill, now used in the manufacture of billions of tonnes of wide-strip steel [6]. Prior to this, the rolling process was by repeatedly passing the steel through a single mill, involving many steps of handling and heating. The original bearing design had an outer forged steel ring and a fixed bronze-bearing race holding steel rollers in position. Modern bearings of this kind would be made entirely of steel although there may be retaining cages which are made from other materials. In spherical roller bearings, the rolling elements are barrel-shaped with two parallel raceways permitting angular contact; the double set permits the bearing to accommodate shaft misalignment.
Taper roller bearings take this concept further by making the rings and rollers tapered, to increase the contact area, permitting large radial and thrust loads. They are for this reason used in some helicopter transmissions to take advantage of their greater load capacity for a given shape or weight when compared with ball or cylindrical roller bearings [7].
In needle roller bearings, the cylinders are long and thin, so that the outer diameter of the bearing is not much greater than that of the inner ring. This makes for a compact design which can be an advantage when space is at a premium. A spherical-roller bearing uses barrelled cylinders as the rolling elements, with two sets of rollers enclosed by the rings. This allows the bearing to accommodate a misaligned load.
Some terminology needed to define directions, and which is used throughout this review, is defined in Fig. 2.
![\includegraphics[width=0.98\linewidth]{directions2.eps}](img79.png)
|
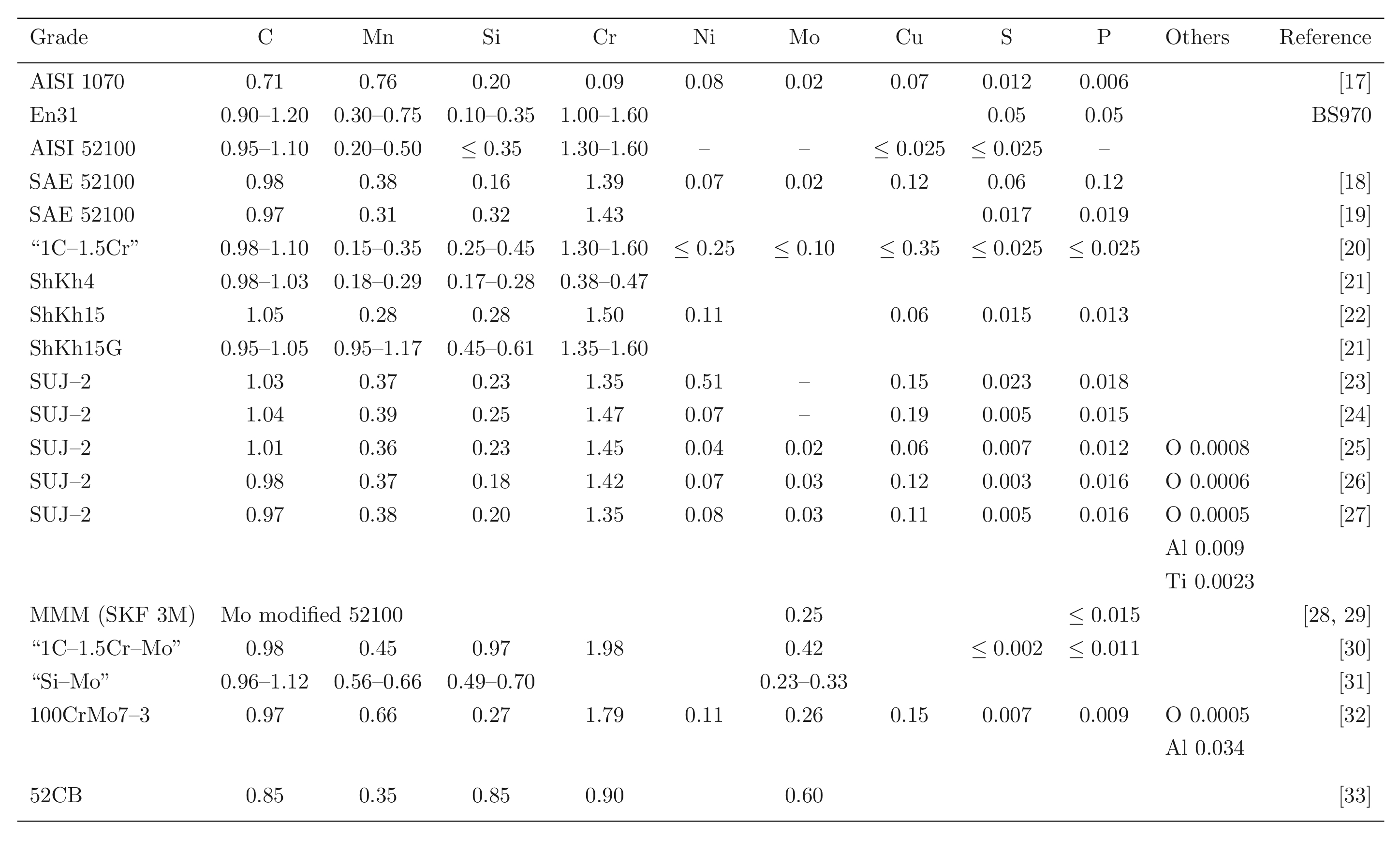
Steels with carbon concentrations in the range 0.8-1.1 wt% and the total substitutional solute content less than 3 wt%, designed originally for machining tools, have historically dominated the mass market for bearings [ s10, 9]. They can be made martensitic by quenching in oil or salt, from a temperature where the material is mostly austenite. However, the focus of this section is on the 1C-1.5Cr type alloys which are extremely popular. Ball bearing tests conducted in 1901 by Stribeck indicated its suitability for the application [11] and was apparently adopted some 120 years ago for bearings by Fichtel & Sachs of Schweinfurt in 1905, and has persisted to this day as a key alloy in the manufacture of bearings [10, 12], with progressive improvements in fatigue performance achieved primarily by improvements in cleanliness with respect to non-metallic inclusions. It represents the majority of the six million tonnes of bearing steel manufactured per annum. The alloy is referred to by numerous national and international designations as indicated in the caption to Table 1; all of these for convenience will henceforth be referred to using the single designation, 52100 typesteel, in the present review.
It is usual for the steel to be supplied in a hot-rolled condition with a pearlitic microstructure including some proeutectoid cementite at the prior austenite grain boundaries, Fig. 3a. The proeutectoid cementite, when it forms networks at the austenite grain boundaries, is undesirable because it has been shown to adversely affect the rolling contact fatigue life in accelerated tests conducted with contact stresses in excess of 5GPa [13]. The networks can be minimised by sufficiently rapid cooling from the final hot-deformation temperature [14], or by annealing to spheroidise the cementite [15], Fig. 3b. As will be discussed later, the relatively large carbon concentration of the steel speeds up the spheroidisation process and is one of the reasons for the success of the steel, that it can be soft annealedwith relative ease. The metallurgy of the spheroidisation process is detailed in section 7. After the appropriate machining or forming, the components are subjected to hardening heat treatments described next.
|
(a)
![\includegraphics[width=0.45\textwidth]{Trojahn3.eps}](img80.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Trojahn4.eps}](img81.png)
|
The calculated equilibrium phase fractions for the mean composition listed as 1C-1.5Cr in Table 1, as a function of temperature, are illustrated in Fig. 4. This is representative of some of the most widely used bearing steels. The calculated [41] equilibrium compositions of austenite and cementite at a typical austenitisation temperature of 840 ![]() C are listed below. An isothermal transformation diagram for austenitisation is shown in Fig. 5[42]. Although the steel becomes fully austenitic at temperatures in excess of about 900
C are listed below. An isothermal transformation diagram for austenitisation is shown in Fig. 5[42]. Although the steel becomes fully austenitic at temperatures in excess of about 900 ![]() C, this is under equilibrium conditions but austenitisation at 1040
C, this is under equilibrium conditions but austenitisation at 1040 ![]() C for 20 min is found in practice to completely dissolve the cementite in 52100 steels containing as much as 1.1 wt% carbon [43]; such a heat treatment results in an austenite grain size of between 40-60 µm 1 . The importance of controlling the austenite grain size to avoid the cracking of 6.
C for 20 min is found in practice to completely dissolve the cementite in 52100 steels containing as much as 1.1 wt% carbon [43]; such a heat treatment results in an austenite grain size of between 40-60 µm 1 . The importance of controlling the austenite grain size to avoid the cracking of 6.
 |
 |
![\includegraphics[width=0.85\textwidth]{equilibrium.eps}](img84.png)
|
Fig. 6 shows how the austenite grain size varies with the austenitisation temperature, with a large increase when carbides are taken into solution at the highest of temperatures. The aluminium has an influence via aluminium nitrides, but only when the austenitisation is conducted in the single ![]() -phase field. Even finer grain sizes can be achieved by rapid heat treatment [45]; although these particular experiments were conducted using molten metal baths, short-duration austenitisation is a reality in commercial induction hardening processing.
-phase field. Even finer grain sizes can be achieved by rapid heat treatment [45]; although these particular experiments were conducted using molten metal baths, short-duration austenitisation is a reality in commercial induction hardening processing.
The kinetics of the cementite dissolution process can be represented by a semi-empirical time-temperature parameter based on Avrami theory [46]. The carbide dissolution process can be accelerated by cold working the steel prior to austenitisation [44]. Because equilibrium is not achieved in commercial heat treatments, there is a degree of superheating necessary above the ![]() temperature in order to induce the formation of austenite; during heating at 2
temperature in order to induce the formation of austenite; during heating at 2 ![]() Cs
Cs ![]() , the austenite begins to form at
, the austenite begins to form at ![]() C and ferrite is eliminated when 790
C and ferrite is eliminated when 790 ![]() C is reached [44].
C is reached [44].
![\includegraphics[width=0.98\linewidth]{Ray_1990b.eps}](img89.png) |
About 3-4 wt% of cementite typically is undissolved at 840 ![]() C, the exact quantity depending on the austenitisation time and the starting microstructure; the cementite in the final microstructure helps improve the resistance of the steel to wear [49]. The cementite also absorbs some of the chromium in the steel, although the level of substitutional solute may not reach that indicated by equilibrium within the time periods involved in industrial processing [50]. Fig. 7shows how the chromium concentration varies with time and temperature; the cementite initially forms rapidly with a composition which is depleted in substitutional solutes and then equilibrates over time [52, 51], as is widely observed in steels for the energy industries [53]. Chromium also raises the
C, the exact quantity depending on the austenitisation time and the starting microstructure; the cementite in the final microstructure helps improve the resistance of the steel to wear [49]. The cementite also absorbs some of the chromium in the steel, although the level of substitutional solute may not reach that indicated by equilibrium within the time periods involved in industrial processing [50]. Fig. 7shows how the chromium concentration varies with time and temperature; the cementite initially forms rapidly with a composition which is depleted in substitutional solutes and then equilibrates over time [52, 51], as is widely observed in steels for the energy industries [53]. Chromium also raises the ![]() temperature so the fraction of cementite is greater relative to a chromium-free steel, at any given temperature within the
temperature so the fraction of cementite is greater relative to a chromium-free steel, at any given temperature within the ![]() phase field [54]. The thermodynamic stability of the cementite is enhanced by enrichment with chromium so that the undissolved particles are able to resist change during heat-treatment and processing [52, 55]. Recent work using X-ray and electron diffraction has indicated that some of the spherical particles assumed to be cementite may in fact be (Fe,Cr)
phase field [54]. The thermodynamic stability of the cementite is enhanced by enrichment with chromium so that the undissolved particles are able to resist change during heat-treatment and processing [52, 55]. Recent work using X-ray and electron diffraction has indicated that some of the spherical particles assumed to be cementite may in fact be (Fe,Cr) ![]() C
C ![]() [56]; the particles were not chemically analysed but their chromium concentrations should be much higher than have been reported in Fig. 7. One difficulty is that (Fe,Cr)
[56]; the particles were not chemically analysed but their chromium concentrations should be much higher than have been reported in Fig. 7. One difficulty is that (Fe,Cr) ![]() C
C ![]() is not a stable phase at the austenitisation temperature used (845
is not a stable phase at the austenitisation temperature used (845 ![]() C), as can be seen in Fig. 4; the discrepancy may be related therefore to chemical segregation in the material and further work is needed where the volume fraction of the chromium-rich carbide can be measured.
C), as can be seen in Fig. 4; the discrepancy may be related therefore to chemical segregation in the material and further work is needed where the volume fraction of the chromium-rich carbide can be measured.
![\includegraphics[width=0.98\linewidth]{Beswick_1988.eps}](img92.png) |
The austenitisation time is typically 20 min so it is an approximation to assume that equilibrium is reached within this time period; the measured kinetics of dissolution are illustrated in Fig. 8. The austenite also becomes depleted in carbon (0.86 wt%), giving a calculated martensite-start temperature [57, 58] of 148![]() C. Subsequent transformations therefore occur from this depleted austenite which has a lower hardenability.
C. Subsequent transformations therefore occur from this depleted austenite which has a lower hardenability.
![\includegraphics[width=0.98\linewidth]{Guillot_1982.eps}](img93.png) |
Quenching from the austenitisation temperature leads to a microstructure containing martensite, about 6vol% of retained austenite [60, 12] and ![]() 3-4% of cementite particles which failed to dissolve during austenitisation. These particles are normally uniformly distributed and have a size of about 0.4-0.6 µm (Fig. 9). The steel is then tempered at approximately 160
3-4% of cementite particles which failed to dissolve during austenitisation. These particles are normally uniformly distributed and have a size of about 0.4-0.6 µm (Fig. 9). The steel is then tempered at approximately 160 ![]() C, a process which may lead to the decomposition of proportion of retained austenite, and to the precipitation of a variety of transition carbides of iron from the supersaturated martensite. These carbides include
C, a process which may lead to the decomposition of proportion of retained austenite, and to the precipitation of a variety of transition carbides of iron from the supersaturated martensite. These carbides include ![]() [61] and
[61] and ![]() [62]. Following the low-temperature tempering treatment, the martensite relies on carbon in solid solution and on fine transition carbides of iron, predominantly
[62]. Following the low-temperature tempering treatment, the martensite relies on carbon in solid solution and on fine transition carbides of iron, predominantly ![]() -carbide (Fig. 10, [63]) for its strength. The material therefore softens during prolonged service at temperatures in excess of about 200
-carbide (Fig. 10, [63]) for its strength. The material therefore softens during prolonged service at temperatures in excess of about 200 ![]() C, which as a consequence is the limit of its maximum service temperature [64]. The bearing is sometimes heated between 80-100
C, which as a consequence is the limit of its maximum service temperature [64]. The bearing is sometimes heated between 80-100 ![]() C in order to interference-fit it on to a shaft; short-term excursions to 225
C in order to interference-fit it on to a shaft; short-term excursions to 225 ![]() C using induction heating have been found to avoid softening even when the steel itself was tempered at 150
C using induction heating have been found to avoid softening even when the steel itself was tempered at 150 ![]() C after martensitic transformation [65]. Work has also been reported on induction tempering, where a 40s excursion to 230
C after martensitic transformation [65]. Work has also been reported on induction tempering, where a 40s excursion to 230 ![]() C is in terms of hardness found to be equivalent to a 1h heat treatment at 150
C is in terms of hardness found to be equivalent to a 1h heat treatment at 150 ![]() C [66].
C [66].
![\includegraphics[width=0.98\linewidth]{Daguier.eps}](img97.png) |
![\includegraphics[width=0.98\linewidth]{Borchers_1969.eps}](img98.png) |
Attempts have been made to reduce the amount of undissolved cementite by decreasing the carbon concentration to 0.77 wt% and maintaining the hardness by solid solution strengthening with silicon and manganese [67] 2 . Although the steel concerned gave comparable fatigue properties in accelerated tests, the industry has persisted with alloys containing some 1 wt% of carbon. One reason is that lower carbon steels are slower to spheroidise [69] and the manufacturing process for bearings requires the steel to be in a soft-annealed condition for certain machining operations. A larger than normal concentration of silicon (0.85 wt%) has also been used in a modified 52100 steel microalloyed with vanadium, with the purpose of reducing the chromium concentration whilst maintaining the hardness and hardenability [71, 70], and a similar approach involving the use of silicon and molybdenum (``Si-Mo", Table 1) [31, 73, 72]. Silicon, by virtue of its low solubility in cementite, retards the low-temperature tempering of martensite [78, 74, 76, 75, 77], and molybdenum through the formation of alloy carbides or their precursors, helps improve the hot-hardness so long as the tempering treatment used permits substitutional solutes to be mobile. The increase in temper-resistance of silicon-enhanced (0.31-1.42 wt%) 52100 steel is said to lead to increased rolling contact resistance, presumably because of the greater hardness for the same level of heat-treatment [79]. Nevertheless, in general the 52100 type alloys reign supreme and substitutes simply do not seem to have been adopted on a comparable scale, presumably because the full set of data necessary for implementation into industrial practice is not available for many of the modified alloys.
The hardenability of the alloy is illustrated in the Jominy curve plotted in Fig. 11, which shows that a depth of at least 5mm can become fully martensitic; the actual hardenability can vary significantly depending on the exact chemical composition within the specification range. The virgin martensite in 52100 with its large carbon concentration is so supersaturated with carbon, that the driving force for precipitation is also large; this is why the hardness of the steel is somewhat sensitive to the quench rate because autotempering of the martensite occurs as it forms at the slower rates [80, 81].
|
(a)
![\includegraphics[width=0.55\textwidth]{Jominy_Drugge.eps}](img100.png) (b) (b) ![\includegraphics[width=0.35\textwidth]{Hewitt_1981.eps}](img101.png)
|
The lower carbon alloy S53C (SAE1053) is used in the manufacture of the rings which form the bearing race for the rolling elements in wheel hub-bearings for automobiles and trucks, Fig. 12. The alloy is cheaper because there is no deliberate addition of chromium and hence also does not require homogenisation after casting. The race surfaces are induction hardened to HRCRockwell C hardness 59 HRC in order to cope with the rigours of rolling contact loads; the contact fatigue life without this hardening is about a third that of the 52100 type steel because the lower carbon content reduces the hardness of the martensite [12]. Another variant of the steel is microalloyed with 0.1 wt% vanadium to improve its strength and toughness in the forged condition. A higher general strength can help reduce the mass of steel required to sustain the design loads [87]. Alloy 1072 is also widely used in the surface induction-hardened condition for hub bearing races, and because of its greater carbon and manganese concentration (Table 1) has a somewhat greater hardenability that S53C.
|
(a)
![\includegraphics[width=0.45\textwidth]{hub.eps}](img102.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Benktander_1981.eps}](img103.png)
|
The 52100 type steels (Table 1) can be made bainitic by isothermal transformation in the temperature range 200-450 ![]() C, with lower bainite dominating the microstructure when the transformation temperature is less than 350
C, with lower bainite dominating the microstructure when the transformation temperature is less than 350 ![]() C [20]. The carbide in the lower bainite is cementite [19], which is in contrast to tempered martensite where it is
C [20]. The carbide in the lower bainite is cementite [19], which is in contrast to tempered martensite where it is ![]() -carbide [90, 63] 3 . The difference arises because there are two demands on the initial excess carbon dissolved in the bainitic ferrite, i.e.,partitioning into the residual austenite and precipitation. When the former dominates, the precipitation is predominantly from carbon-enriched austenite [93]. The lower bainitic microstructure observed in 52100 following isothermal transformation at 230
-carbide [90, 63] 3 . The difference arises because there are two demands on the initial excess carbon dissolved in the bainitic ferrite, i.e.,partitioning into the residual austenite and precipitation. When the former dominates, the precipitation is predominantly from carbon-enriched austenite [93]. The lower bainitic microstructure observed in 52100 following isothermal transformation at 230 ![]() C is illustrated in Fig. 13, [94].
C is illustrated in Fig. 13, [94].
![\includegraphics[width=0.98\linewidth]{Vetters_2006.eps}](img104.png) |
A measured time-temperature transformation diagram for 52100 steel is illustrated in Fig. 14 4 . Fig. 15shows an alternative diagram, plotted on the same horizontal scale for an almost identical steel which has been austenitised at a lower temperature so that the carbon concentration in the austenite would be reduced; the consequent increase in driving force for transformation leads to an acceleration of the bainite reaction [95]. On the other hand, the formation of pearlite< /a> is faster when the austenitisation temperature is greater ( cf.Figs 14& 15) because of the larger concentration of carbon dissolved in the austenite. A continuous cooling transformation diagram is shown in Fig. 16, illustrating the change in ![]() when martensite is preceded by partial transformation to bainite, due to the enrichment of the residual austenite with partitioned carbon.
when martensite is preceded by partial transformation to bainite, due to the enrichment of the residual austenite with partitioned carbon.
The complete transformation to bainite at a temperature just above ![]() ( i.e.,
( i.e., ![]() C) can take some 4 h, which adds to the expense of heat-treatment when compared with the quenched and tempered condition 5 . It is possible to accelerate the reaction by first quenching to a temperature about 20
C) can take some 4 h, which adds to the expense of heat-treatment when compared with the quenched and tempered condition 5 . It is possible to accelerate the reaction by first quenching to a temperature about 20 ![]() C below
C below ![]() for less than a minute, and then raising it into the bainite range [94]. Step quenching of this kind, but within the bainite transformation range has been known for some time to accelerate the transformation kinetics at the higher temperature [99, bainite" id="tex2html414">100, 98, 97]. It has been demonstrated experimentally that the two-step treatment of bearing steel can shorten the heat-treatment time without sacrificing hardness [103, 101, 102, 94], but it remains to be proven that the process can be adapted to industrial practice. As an example, the complete transformation of 52100 steel at a constant 210
for less than a minute, and then raising it into the bainite range [94]. Step quenching of this kind, but within the bainite transformation range has been known for some time to accelerate the transformation kinetics at the higher temperature [99, bainite" id="tex2html414">100, 98, 97]. It has been demonstrated experimentally that the two-step treatment of bearing steel can shorten the heat-treatment time without sacrificing hardness [103, 101, 102, 94], but it remains to be proven that the process can be adapted to industrial practice. As an example, the complete transformation of 52100 steel at a constant 210 ![]() C takes 33 h, after which the hardness achieved is 60.1 HRC; by transforming the majority of the austenite at the same temperature but for 9h, followed by heating to 250
C takes 33 h, after which the hardness achieved is 60.1 HRC; by transforming the majority of the austenite at the same temperature but for 9h, followed by heating to 250 ![]() C for 1 h, results in a completely bainitic microstructure with a slightly reduced hardness of 59.9 HRC [101].
C for 1 h, results in a completely bainitic microstructure with a slightly reduced hardness of 59.9 HRC [101].
It has been argued that a somewhat softer lower bainitic structure in the 52100 steel outperforms martensite when hydrogen embrittlement is an issue, because of its greater toughness and ductility [104] 6 . This is consistent with independent work on which the time at the austenitisation temperature was controlled to obtain different fractions of undissolved cementite; changing the fraction from 0.09 to 0.01 led to an increase in strength due to the greater carbon concentration in solution within the martensite, causing a deterioration in toughness and fatigue resistance [106]. On a similar rationale, pearlite< /a> and upper bainite are avoided since they apparently reduce fatigue life [20].
One advantage of a bainitic microstructure with its constituent carbides, is that the reaction in bearing steels such as 52100 is able to progress until almost all of the austenite is consumed. It follows that the retained austenite content is minimal at about 1vol.% [107] so that isothermally transformed structures of these kind are dimensionally stable. The heat treatments typical in the production of bainite also help minimise the possibility of quench cracking [107].
![\includegraphics[width=0.98\linewidth]{TTT.eps}](img106.png) |
![\includegraphics[width=0.98\linewidth]{TTT_Vetters.eps}](img107.png) |
![\includegraphics[width=0.98\linewidth]{Brandis.eps}](img108.png) |
The same steel is often used for both the bearing raceway and the rolling elements. Early studies of how small differences in hardness of 52100 steel, between the rolling element and the raceway, influence the development of residual stress and sub-surface hardness during rolling contact, have indicated an influence but not revealed systematic trends [111, 109, 110]. No correlation could be found between changes in hardness, the initial differential hardness and fatigue life. Furthermore, the physical mechanisms of such effects need to be clarified; the important point is that potential effects should be controlled in tests designed to measure stresses. More recent work [112] tends to suggest that rolling elements should be some 2 HRC harder in order to achieve the best rolling contact fatigue life, Fig. 17.
![\includegraphics[width=0.98\linewidth]{Neale_1973.eps}](img109.png) |
The total concentration of an impurity, for example oxygen, does not necessarily determine the mechanical properties, but rather, how the impurity is distributed in the steel. Thus, there is a dependence of rolling contact fatigue life against the length of strings of inclusions [113]. There are nevertheless, correlations of fatigue performance against the total oxygen concentration [113, 115, 114] so it is valid to examine concentration as a parameter whilst bearing in mind that there will be noise in any interpretation based on total measures. Almost all the oxygen in solidified steel is present as oxides [117, 116] which are the key culprits in the processes which lead to the initiation of damage during repeated loading. This is why unlike many other technologies, the concentration of oxygen in modern bearing steels must be limited to less than 10 ppmw [118, 119], Table 2. The accuracy with which the concentration can be reproduced in practice is about ![]() ppmw [116] and there can exist a real range in the mean concentration within an ingot by some 2-5 ppmw [120]. The variance in oxygen measurements seems to become larger as the mean concentration increases [121].
ppmw [116] and there can exist a real range in the mean concentration within an ingot by some 2-5 ppmw [120]. The variance in oxygen measurements seems to become larger as the mean concentration increases [121].
| Steel Product | Maximum concentration / ppmw | ||
| Oxygen | Nitrogen | Hydrogen | |
| Automotive sheet | 30 | ||
| Drawn and ironed cans | 20 | 30 | |
| Line pipe | 30 | 50 | |
| Ball bearings | 10 | ||
| Tire cord | 15 | 40 | 2 |
| Heavy plate | 20 | 40 | 2 |
| Wire | 30 | 60 | |
Titanium is not a deliberate addition to the standard bearing steel (52100 type), but is present in small concentrations, typically 0.0025 wt%, primarily through the use of ferro-alloys (ferro-chromium in particular [117]) or from scrap [122] used in the steel manufacturing process. It may be introduced through the reduction of titanium oxide in the slag during basic oxygen steelmaking, especially when there is a substantial amount of aluminium dissolved in the melt [123, 124]. Titanium carbides and carbonitrides are known to initiate fatigue cracks in axially loaded or rotating-bending fatigue experiments (Fig. 79, [125]) and there is limited evidence in the context of rolling contact fatigue [126]. Indeed, it is said that Ti(C,N) particles of the same size and position as oxides do not induce the formation of butterflies [127]. This may be related either to the strength of the interface between the carbonitride and the matrix, or that the particles are more resistant to fracture and hence less effective in nucleating cracks which propagate into the matrix. The nitrogen concentration must be limited to ![]() ppmw in order to avoid titanium nitride formation [128].
ppmw in order to avoid titanium nitride formation [128].
Table 3lists the lower limits in impurity concentrations said to be achievable in commercial reality. Although a practical limit to the total hydrogen content is probably about 1 ppmw, electron beam melted 52100 type steel has been shown to contain as little as 0.4 ppmw [22].
It has been speculated that interstitial nitrogen and nitrides can in the 52100 type bearing steels pin dislocations and hence reduce the ability to relax stresses, thereby leading to a reduction in the rolling contact fatigue life [129, 130]. Concentrations of total nitrogen are in the range 15-100 ppmw. Further work is needed to understand the mechanism since the correlations of properties against nitrogen content are based on the total concentration rather than that in solution [131]; some of the total may be tied up as nitrides. It is established that blowing liquid steel with nitrogen degrades the fatigue resistance and toughness of the 52100 type steels when compared with the use of argon for this purpose [132]. On the other hand, nitrogen concentrations up to 150 ppmw in M50 secondary hardening steel are not considered to be an important liability [133].
| Solute | P | C | S | N | H | O | Ti |
| Concentration / ppmw | 10 | 5 | 5 | 10 | 3 | 10 |
The average total-hydrogen concentration of 52100 steel following manufacture into a bar with a diameter just over 15mm can be as large as 8 ppmw. The concentration is not uniform but varies between 7-15 ppmw in the vicinity of the surface and diminishes to some 0.5-2.5 ppmw towards the core [135]. These are quite large concentrations which would normally be acceptable in the final bearing, so it is presumed that subsequent manufacturing processes lead to reductions in hydrogen concentration. The gaseous-impurity concentrations typically achieved during a variety of bearing-steel processes are listed in Table 4.
| Process | Hydrogen | Nitrogen | Oxygen |
| Air melting + vacuum degassing | 3.2 | 120 | 46 |
| Air melting | 4.8 | 150 | 67 |
| + 1 vacuum arc remelt | 1.8 | 80 | 37 |
| + 2 vacuum arc remelts | 60 | 9 | |
| + 3 vacuum arc remelts | 50 | 5 | |
| Vacuum induction melting | 85 | 21 | |
| Vacuum induction melting + | |||
| vacuum arc remelting | 60 | 6 |
Sulphur manifests within the steel in the form of compounds, particularly manganese sulphide. The sulphides can form in isolation or deposit on to existing oxide particles, with the fraction of oxides encapsulated by sulphides increasing as the oxygen concentration is reduced [122]. The sulphur concentration is controlled during the ladle treatment of molten steel by partitioning from the melt and from the atmosphere within the ladle, into the slag [136]. The partial pressure of sulphur and oxygen during this stage is less than 10 ![]() atm and gaseous sulphur then replaces oxide ions in the slag to release oxygen and in the process becomes entrapped within the slag. Similarly, sulphur dissolved in the metal is captured as it substitutes for oxide ions in the slag. The capacity of a slag to absorb sulphur is thus given by the product
atm and gaseous sulphur then replaces oxide ions in the slag to release oxygen and in the process becomes entrapped within the slag. Similarly, sulphur dissolved in the metal is captured as it substitutes for oxide ions in the slag. The capacity of a slag to absorb sulphur is thus given by the product ![]() where
where ![]() represents the partial pressure of the gaseous species concerned. This capacity correlates well with the basicity of the slag, most simply defined as the ratio of the basic oxide CaO to acidic oxide SiO
represents the partial pressure of the gaseous species concerned. This capacity correlates well with the basicity of the slag, most simply defined as the ratio of the basic oxide CaO to acidic oxide SiO![]() . Specific additions of lime help to remove sulphur via the reaction
. Specific additions of lime help to remove sulphur via the reaction ![]() .
.
The role of sulphides in the 52100 type bearings steels has been a somewhat confused. Sulphides have been known for a long time to increase machinability by acting as chip-breakers. Some papers suggest that the expansion coefficient of MnS is less than that of iron [137] whereas others explain the insensitivity of rolling contact fatigue strength to sulphur concentration by assuming that the coefficient is relatively large, so that tensile stresses do not develop around the inclusion [138]. Early work has even suggested that concentrations in the range 0.013-0.043 wt% result in an improvement in fatigue performance because the sulphides coat the relatively brittle oxides present in 52100 type steels [143, 140, 142, 139, 141]; the sulphides have also been suggested to act as barriers to the propagation of damage (butterflies, section 21.2.3) originating at alumina particles [144]. This is unlikely to be the case with modern bearing steels which have much higher levels of overall cleanliness. Indeed, it has been pointed out that a minimum sulphur content is appropriate for optimum fatigue resistance in steels containing low concentrations of oxides and titanium compounds [136, 145]. Sulphide particles tend to be plastic during hot-deformation and any detrimental effect is mitigated by large reduction ratios [146]. All kinds of inclusions can be expected to contribute to the initiation of cracks when the contact stresses are very large, such as those used to accelerate tests ( ![]() MPa) [147]. Excessive local concentrations of sulphides or oxysulphides can lead to low melting-temperature eutectics which then compromise the ability to hot-deform the steel [148].
MPa) [147]. Excessive local concentrations of sulphides or oxysulphides can lead to low melting-temperature eutectics which then compromise the ability to hot-deform the steel [148].
There are many processes that can be used to alter the properties of the steel at its surface. For example, 52100 steel can be laser treated to produce a surface hardness in excess of 1000 HV [105, 149, 150]. When the laser conditions are such that surface melting occurs, 52100 steel solidifies into a structure consisting of ledeburite eutectic, large quantities of retained austenite and martensite; this mixture is not considered to be optimum from the point of view of rolling contact fatigue [105]. Laser glazing, in which the surface is rapidly heated and re-solidified also results in a hard structure to a depth of about 100 µm and has been used in alloys such as M1 to eliminate the coarse carbides that result from conventional solidification, and to introduce a compressive stress at the surface [151]. Ion implantation of 52100 steel with carbon beyond a critical dose has been shown to lead to a virtually zero wear rate in pin-on-disc tests; the implantation left much of the carbon in solid solution with the remainder as ![]() -carbide, without introducing additional retained austenite [152]. Nitrogen implantation also increases the hardness and induces a compressive stress extending many tens of micrometres into the surface of 52100 steel [153]. Titanium implantation to a depth of about 0.1 µm changes the friction characteristics and adhesive wear behaviour [154], although the detailed mechanisms responsible for these changes do not seem to have been investigated.
-carbide, without introducing additional retained austenite [152]. Nitrogen implantation also increases the hardness and induces a compressive stress extending many tens of micrometres into the surface of 52100 steel [153]. Titanium implantation to a depth of about 0.1 µm changes the friction characteristics and adhesive wear behaviour [154], although the detailed mechanisms responsible for these changes do not seem to have been investigated.
This section deals, however, with processes that change the chemical composition of the surface to a depth extending a millimetre or so, such that the lower carbon concentration of the core gives greater toughness in circumstances where structural integrity can otherwise be compromised. Case carburised, nitrided or carbonitrided components have the advantage of a hard surface metallurgically bonded to a tough core. Carburising also introduces a compressive stress ( ![]() MPa) in the surface, resulting in an improvement in fatigue performance [155]; this combination makes surface-hardened raceways more resistant to indentation when compared against through-hardened bearings [156]. Whereas both through hardened and surface hardened steels can serve well in ordinary applications where rolling contact fatigue or wear are the prime concerns, case hardened bearings because of their tough cores serve better in circumstances where bending, torsion and impact stresses have to be resisted [157]. Surface modified bearings are therefore used widely in automotive applications, or when large bearings with diameters in excess of 3m have to be made where it is impractical to expect through-hardening. It is argued that in addition to the residual stresses, the partial transformation of retained austenite into martensite during cyclic loading leads to hardening which contributes to the improved resistance in four-point bending fatigue tests [155].
MPa) in the surface, resulting in an improvement in fatigue performance [155]; this combination makes surface-hardened raceways more resistant to indentation when compared against through-hardened bearings [156]. Whereas both through hardened and surface hardened steels can serve well in ordinary applications where rolling contact fatigue or wear are the prime concerns, case hardened bearings because of their tough cores serve better in circumstances where bending, torsion and impact stresses have to be resisted [157]. Surface modified bearings are therefore used widely in automotive applications, or when large bearings with diameters in excess of 3m have to be made where it is impractical to expect through-hardening. It is argued that in addition to the residual stresses, the partial transformation of retained austenite into martensite during cyclic loading leads to hardening which contributes to the improved resistance in four-point bending fatigue tests [155].
The depth of hardening is usually less than 1mm, although greater penetration may be required if the bearing surface requires extensive grinding following heat-treatment. The properties of the core can be adversely affected by the abnormal growth of austenite grains during heat-treatment so microalloying with vanadium has been proposed as a solution [34]. The chemical composition is listed in Table 1and relies on the precipitation of V(C,N) which pins the austenite grains to a size of about 22 µm on treatment at 930 ![]() C for 5 h. For the same reason, microalloying with aluminium and nitrogen, or niobium, leads to an improvement in the rolling contact fatigue life of carburised surfaces when the primary failure mechanism is by the propagation of cracks along the austenite grain boundaries [158, 159]. The size can also be controlled and refined by repeated austenitisation and quenching ( e. g. double hardening) [160]. The double hardening is now routinely implemented for case-carburised bearings [161].
C for 5 h. For the same reason, microalloying with aluminium and nitrogen, or niobium, leads to an improvement in the rolling contact fatigue life of carburised surfaces when the primary failure mechanism is by the propagation of cracks along the austenite grain boundaries [158, 159]. The size can also be controlled and refined by repeated austenitisation and quenching ( e. g. double hardening) [160]. The double hardening is now routinely implemented for case-carburised bearings [161].
Carbonitrided samples contain significant concentration gradients with corresponding variation in the quantity of retained austenite as a function of depth. The region in close proximity to the free surface retains the most austenite and hence is in a relatively soft condition, Fig. 18; if austenitisation subsequent to surface treatment leads to decarburisation then the softening of the surface can be a result of decarburisation, in which case the retained austenite content at the surface would also be reduced [162]. A re-hardening heat treatment can lead to some homogenisation of the interstitial solutes, thus restoring the hardness on quenching, Fig. 18b.
|
(a)
![\includegraphics[width=0.45\textwidth]{Lee_2007b_austenite.eps}](img118.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Lee_2007b_hardness.eps}](img119.png)
|
Whereas case-hardened bearings can lead an optimum gradient in properties for onerous applications, the production process is necessarily more complex and expensive when compared with through-hardened bearings. In M50NiL, the carburising process has been shown to lead to small changes in bearing ring dimensions which may add to subsequent distortions caused by heat-treatment [163]. The additional cost may not the determining factor when it comes to aerospace bearings; alloys suitable for case hardening and service at elevated temperatures are discussed in detail in section 8.
Steels designed for through-hardening may also be induction hardened, a treatment which is relatively cheap, can routinely produce a surface hardness of 60 HRC in 52100 type steels. Because of its short duration the process is not associated with significant decarburisation. The time for the induction treatment can range from seconds for balls and rollers, to several minutes for bearing rings some 2m in diameter, whose surfaces rotate through a stationary induction coil [164]. The austenitisation treatment ( ![]() C) takes about 60s or less, after which the component is quenched - the austenite grain size in the treated region is therefore relatively fine, resulting in better toughness [21]. Selected regions of the sample can be hardened and complex shapes are possible using multiple frequency induction. It is not obvious from the literature whether the process is sensitive to the composition of the steel as long as the hardenability is sufficient given the typical cooling rates involved. However, as will be seen in section 18.3, the residual stress profile that results from the induction treatment can be a function of the hardenability of the steel.
C) takes about 60s or less, after which the component is quenched - the austenite grain size in the treated region is therefore relatively fine, resulting in better toughness [21]. Selected regions of the sample can be hardened and complex shapes are possible using multiple frequency induction. It is not obvious from the literature whether the process is sensitive to the composition of the steel as long as the hardenability is sufficient given the typical cooling rates involved. However, as will be seen in section 18.3, the residual stress profile that results from the induction treatment can be a function of the hardenability of the steel.
Plasma-immersion ion implantation has been used to introduce nitrogen into the surface of 52100 steel. To achieve a hardness in excess of 800HV requires the steel to be heated to 500 ![]() C for some 3-5h in order to obtain hardening to a depth of about 40 µm [165]. Surprisingly, the increase in surface hardness is due to the formation of iron nitrides rather than chromium nitrides which ought to be more stable. It is possible that the chromium concentration is insufficient in 52100 steel, which is not designed for this purpose.
C for some 3-5h in order to obtain hardening to a depth of about 40 µm [165]. Surprisingly, the increase in surface hardness is due to the formation of iron nitrides rather than chromium nitrides which ought to be more stable. It is possible that the chromium concentration is insufficient in 52100 steel, which is not designed for this purpose.
The rather shallow nature of the plasma implantation raises difficulties because in practice, damage is most pronounced deeper into the steel during rolling contact. On the other hand, independent work on the hard turning of the same steel, found that a compressive stress over a depth of 50 µm, induced by the machining, reduced the propensity for spalling, presumably because buried cracks then find it more difficult to break the surface [167, 166]. However, this interpretation may be uncertain given that the inner races were honed prior to testing, a process which would definitely modify the state of stress at the surface [168]. More work is needed to understand the influence of shallow surface treatments on bearing life, because it is found in comparisons between treated and non-treated bearing raceways, that both of them end up with a similar pattern of residual stress after being exposed to rolling contact cycles [166].
Steels such as 52100 steel when in a typically quenched and tempered condition are not particularly ductile; the elongation in tension is barely 1-2% so meaningful tensile test data are difficult to come by and hardness or bending strength is often reported instead. Hardness in the range 59-66 HRC has been shown to correlate positively with rolling contact fatigue life and greater hardness is associated with reduced wear in the bearing tracks [169]; this correlation of wear against hardness fails in tests involving the unlubricated sliding of 52100 steel against a much harder ring [170] because of the effects of heat generation on material removal.
Tensile tests do contain a wealth of information not accessible from hardness data; for example, the reduction of area and ultimate tensile strength feature in the rationalisation of uniaxial fatigue tests [171]; the elongation and proof strength similarly feature in the estimation of fatigue crack growth rates [172, 174, 173]. The reduction of area measured at ambient temperature has been reported at less than 0.5% [175]; some temperature-dependent properties are listed in Table 5. The 52100 steel is not intended for elevated temperature service but the data are nevertheless useful in finite element analysis of machining processes. Fig. 19 shows typical values of the bending strength for a variety of microstructures [176]; the stresses involved are large and it is difficult to see how these can be interpreted in an applicable manner. It is not clear, for example, why the hardness shows a trend which is opposite to the bending strength as the microstructure is varied. The fact that the mixed microstructures are stronger than the fully martensitic sample is not significant because the former also contained untempered martensite.
| Temperature / |
20 | 200 | 400 | 600 | 800 |
| Yield strength / MPa | 1394 | 1161 | 908 | 414 | 303 |
| Ultimate tensile strength / MPa | 1748* | 2151 | 1551 | 934 | 311 |
| Reduction of area / % | 1.0* | 2.0 | 1.6 | 1.5 | 1.0 |
| Young's modulus / GPa | 208 | 163 | 154 | 113 | 103 |
![\includegraphics[width=0.98\linewidth]{prequench.eps}](img121.png) |
Some general statements indicate that 52100 steel in its usual martensitic condition (with 11% ![]() ) or when transformed to lower bainite at temperatures below 300
) or when transformed to lower bainite at temperatures below 300 ![]() C (without
C (without ![]() ), exhibit a 0.2% proof strength in the range 1400-2200 MPa and an ultimate tensile strength between 2150 and 2450 MPa [178]. The higher values correspond to martensite and the strength decreases as the bainite transformation temperature is increased. Some specific data for the influence of the bainite transformation temperature are illustrated in Fig. 20. The ductility in the bainitic condition is always larger than the minimal plasticity exhibited by the tempered martensite structure in this steel; this may explain why the life of lower bainitic bearings operating in water-containing environments exceeds that of quenched and tempered varieties [179].
), exhibit a 0.2% proof strength in the range 1400-2200 MPa and an ultimate tensile strength between 2150 and 2450 MPa [178]. The higher values correspond to martensite and the strength decreases as the bainite transformation temperature is increased. Some specific data for the influence of the bainite transformation temperature are illustrated in Fig. 20. The ductility in the bainitic condition is always larger than the minimal plasticity exhibited by the tempered martensite structure in this steel; this may explain why the life of lower bainitic bearings operating in water-containing environments exceeds that of quenched and tempered varieties [179].
![\includegraphics[width=0.98\linewidth]{Kerscher.eps}](img123.png) |
Fig. 21illustrates plots of the true compressive strength against the true strain in compression, for a variety of tempering temperatures [182]. Compressive strength is of course relevant in bearing applications, since the resultant shear is what leads to damage accumulation. The data are as expected, since more of the carbon should be retained in solid solution within the martensite as the tempering temperature is reduced. It is interesting that the form of the stress versus strain curve changes with a reduction in the rate of work hardening as the tempering temperature ![]() is increased. Some of this reduction may be associated with the fact that the amount of retained austenite in the microstructure decreases as the
is increased. Some of this reduction may be associated with the fact that the amount of retained austenite in the microstructure decreases as the ![]() is increased [60] because the stress-induced transformation of such austenite enhances the work-hardening rate. However, it is also well known that stronger steels work harden more rapidly because they contain a greater number density of obstacles to dislocation glide. A work hardening exponent defined as
is increased [60] because the stress-induced transformation of such austenite enhances the work-hardening rate. However, it is also well known that stronger steels work harden more rapidly because they contain a greater number density of obstacles to dislocation glide. A work hardening exponent defined as ![]() for
for ![]() is in the range 0.06-0.1 depending on the heat treatment and retained austenite content [182].
is in the range 0.06-0.1 depending on the heat treatment and retained austenite content [182].
A more comprehensive description of strength, as a function of temperature, strain and strain rate is required for the purposes of finite element modelling, for example in the numerical simulation of machining. Umbrello et al.have created precisely such a framework for steel 52100, which seems to work well in empirically representing the constitutive behaviour of the alloy over a wide range of conditions [183]. Oddly, they also included hardness as a parameter in the functional for flow stress, on the basis that it is a parameter which is important in the characterisation of machinability since tool wear becomes significant when the hardness exceeds about 45 HRC. However, their interpretation of hardness is unconventional, that it is a consequence of heat treatment and independent of mechanical work. Although this is an inconsistency, the method is adequate for the purpose of numerical modelling presumably because the work hardening coming from mechanical work is handled separately in the grand scheme.
![\includegraphics[width=0.98\linewidth]{compression_Sickels.eps}](img128.png) |
Some unusual heat and thermomechanical treatments have been used in an attempt to improve the homogeneity, ease of spheroidisation, tensile ductility and toughness of 52100 type steels [184, 185]. The experimental design was based largely on the notion that carbides within the structure, which do not dissolve during austenitisation, are detrimental to these particular properties. The heat treatments were therefore more complex, as follows:
![\includegraphics[width=0.98\linewidth]{Garg_1986.eps}](img129.png) |
Data are not available for properties such as rolling contact fatigue for the steel in these special conditions. In a case where RCF was in fact measured [185], finer cementite dispersions obtained by first transforming the steel to pearlite< /a> at 650 ![]() C, reaustenitising at 900
C, reaustenitising at 900 ![]() C and then implementing the quenched and tempered state, led to an improvement in fatigue life. It was concluded that it is not necessary to dissolve all of the cementite in order to optimise the fatigue life.
C and then implementing the quenched and tempered state, led to an improvement in fatigue life. It was concluded that it is not necessary to dissolve all of the cementite in order to optimise the fatigue life.
Another unusual heat-treatment aims at stabilising the retained austenite [91]. After quenching to ambient temperature, the steel is held below ![]() at
at ![]() C for a prolonged period of 10h in order to allow some of the retained austenite to transform isothermally into martensite. This apparently stabilises the remaining austenite to both sub-zero treatment, subsequent tempering and deformation. The deformation associated with the formation of isothermal martensite is said to introduce dislocations in the remaining austenite which mechanically stabilises the phase [195, 194]. Isothermal martensite is rarely discussed in the bearing steel literature but its mechanism and microstructural characteristics are well established in the wider literature [198, 196, 199, 200, 197].
C for a prolonged period of 10h in order to allow some of the retained austenite to transform isothermally into martensite. This apparently stabilises the remaining austenite to both sub-zero treatment, subsequent tempering and deformation. The deformation associated with the formation of isothermal martensite is said to introduce dislocations in the remaining austenite which mechanically stabilises the phase [195, 194]. Isothermal martensite is rarely discussed in the bearing steel literature but its mechanism and microstructural characteristics are well established in the wider literature [198, 196, 199, 200, 197].
As described in section 1, the carbon concentration of the austenite in 52100 steel following a typical austenitisation heat treatment is less than 0.86 wt%. It is therefore not particularly strong, as shown by the data in Table 6, even at low temperatures, compared with the overall strength of the steel in its quenched and tempered condition. This means that during deformation, any retained austenite will accommodate more plastic strain than the remainder of the microstructure which is much harder [202, 201], and transform into stress- or strain-induced martensite during the early stages of service. Cyclic deformation tests described in section 5.3 show that much of the retained austenite decomposes into martensite during the very first cycle.
The austenite in such bearing steels is in contrast to the much higher carbon retained austenite found in association with bainite in silicon-containing steels where it is in fact the hardest phase in the structure [203] and hence is much more stable during plastic deformation [204].
| Temperature / |
300 | 400 | 700 | 800 |
| 0.2% proof strength / MPa | 292 | 277 | 92 | 78 |
It is reported [205] that austenite in 52100 steel exhibits a Bauschinger effect whereby plastic deformation becomes easier when the sense of strain is reversed. The intensity of the Bauschinger effect increases when the supercooled austenite is subjected to reversed loading at lower temperatures. The exact mechanism of the effect has not been revealed but is speculated, for example, to be either because of damage accumulating at the undissolved carbides present in the austenite during the first loading, or because of the temperature dependency of the stacking fault energy of austenite. Identical tests conducted on the steel austenitised at a higher temperature to dissolve all the cementite would be informative. It is not obvious how this information can be exploited in constitutive modelling or the calculation of distortion and residual stress.
A large part of the shaping of bearing steels consists of hot deformation carried out in several stages of reduction. Fig. 23a shows how the stress and strain behaviour of the austenite changes in a simulated hot-deformation process [14]. More comprehensive isothermal compression data extending to larger strains [207, 206] covering strain rates in the range 0.1-10 s ![]() and 950-1150
and 950-1150 ![]() C show that for all of these conditions, the austenite in 52100 steel dynamically recrystallises during deformation. This can be deduced from the fact that the compressive stress versus strain curve exhibits a peak followed by softening associated with recrystallisation (there are some recent metallographic data to support this conclusion [208]). The peak stress (
C show that for all of these conditions, the austenite in 52100 steel dynamically recrystallises during deformation. This can be deduced from the fact that the compressive stress versus strain curve exhibits a peak followed by softening associated with recrystallisation (there are some recent metallographic data to support this conclusion [208]). The peak stress ( ![]() ) in the stress versus compressive strain is, for these experiments, given in a standard empirical form commonly used to describe constitutive relations:
) in the stress versus compressive strain is, for these experiments, given in a standard empirical form commonly used to describe constitutive relations:
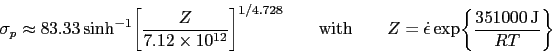 |
(1) |
|
(a)
![\includegraphics[width=0.55\textwidth]{Gembalova_2007.eps}](img135.png) (b) (b) ![\includegraphics[width=0.35\textwidth]{Zhu_2008.eps}](img136.png)
|
In an interesting study where 52100 steels is repeatedly cycled through the
![]() transformation with the material under a static tensile stress
transformation with the material under a static tensile stress ![]() MPa, Oelschlägel and Weiss [211] observed an elongation in excess of 500% prior to fracture. This comes from the accumulation of transformation plasticity over the 260 cycles utilised. They labelled the phenomenon as `superplasticity' which in modern terminology involves grain boundary diffusion and grain rotation.
MPa, Oelschlägel and Weiss [211] observed an elongation in excess of 500% prior to fracture. This comes from the accumulation of transformation plasticity over the 260 cycles utilised. They labelled the phenomenon as `superplasticity' which in modern terminology involves grain boundary diffusion and grain rotation.
It is useful in the context of bearing steels to study cyclic stress-strain behaviour because the work hardening behaviour in the early stages of deformation defines the shakedown limit. The information may also be exploited in the elastic strain based Hertzian treatment of rolling-contact stresses into the elastic-plastic regime. Fig. 24 shows the cyclic stress-strain behaviour of 52100 steel in its quenched and tempered martensitic condition but containing 11% of retained austenite [29]. The net elongation of the sample after the completion of the first cycle, as indicated by the failure of the loop to close, is largely a consequence of the transformation of the majority of retained austenite during the first application of the tensile stress. Only 4% of the austenite remains after the first cycle and this quantity does not diminish significantly with further cycles 7 . Subsequent loops show ever decreasing closure failure, and are essentially closed after about five cycles. This is because the material cyclically hardens, so that in a test where the stress amplitude is maintained constant, the degree of macroscopic plasticity detected decreases, as is evident from the loop illustrated for the 200th cycle. In contrast, when the strain amplitude is maintained constant, the stress required increases empirically as ![]() MPa, where
MPa, where
![]() is the plastic strain range [212].
is the plastic strain range [212].
In contrast to the behaviour of 52100 steel in its martensitic condition, softening is observed to occur in the early stages of cycling when the microstructure is bainitic with very little retained austenite in the initial state.
![\includegraphics[width=0.98\linewidth]{Christ_loops.eps}](img142.png) |
Notice that the loops illustrated in Fig. 24have an unconventional shape once the austenite is rendered innocuous. This shape is often described as that of a `sickle', as opposed to one which is symmetrical about the zero stress and zero strain point. The peculiar shape is the outcome of non-linear elasticity exhibited by 52100 steel both in the martensitic and bainitic conditions [213, 178]. It is well known [214, 215] that iron at very large stresses shows deviations from Hooke's law when the elastic strain exceeds about 1-2%. The deviation is expected because the way in which the force between atoms varies as a function of interatomic spacing is not symmetrical as the force changes sign (an anharmonic lattice potential). The stress-strain relationships become
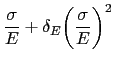 |
(2) |
| Microstructure | |||
| Bainitic | |||
| Martensitic |
The hardness of of 52100 type steels can be estimated using a rule of mixtures with the assumption that the hardnesses of martensite, bainite, pearlite< /a> and austenite are given by 64, 35, 29 and 17 HRC [217] 8 The method is likely to be reasonably accurate as long as the steel does not contain much bainite because it is unreasonable to assign a single value of 35 HRC to this phase since isothermal transformation to a fully bainitic structure at 250 ![]() C following austenitisation at 840
C following austenitisation at 840 ![]() C leads to a hardness close to 60 HRC [218]. The concept is inconsistent with the data presented in Fig. 19. On the other hand, transformation at 290
C leads to a hardness close to 60 HRC [218]. The concept is inconsistent with the data presented in Fig. 19. On the other hand, transformation at 290 ![]() C leads to a hardness of between 38-39 HRC [219].
C leads to a hardness of between 38-39 HRC [219].
The tempering time to reach an equivalent hardness during low-temperature heat treatment has been expressed as an equivalence parameter in the context of 52100 type steels,
| (3) |
Increasing the austenitisation temperature when heat treating 52100 steel does not, beyond about ![]() C, increase the hardness of the quenched or quenched and tempered structure, Fig. 25[221]. This is because although the carbon concentration of the austenite, and hence of the martensite that forms on quenching, increases, so does the amount of relatively soft retained austenite. Even this conclusion is not completely safe since the hardness of martensite ceases to increase as a function of its carbon concentration once about 800HV has been achieved [223, 222].
C, increase the hardness of the quenched or quenched and tempered structure, Fig. 25[221]. This is because although the carbon concentration of the austenite, and hence of the martensite that forms on quenching, increases, so does the amount of relatively soft retained austenite. Even this conclusion is not completely safe since the hardness of martensite ceases to increase as a function of its carbon concentration once about 800HV has been achieved [223, 222].
|
(a)
![\includegraphics[width=0.45\textwidth]{Huh_a.eps}](img162.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Huh_b.eps}](img163.png) (c) ![\includegraphics[width=0.45\textwidth]{Hokkirigawa_1988.eps}](img164.png)
|
Cold forging components into approximate shape can minimise the costs associated with machining, as long as the process does not involve large stresses and assuming that wear on dies is not the cost-determining factor. The ability to cold-forge bearing steels is related approximately to its compressive strength; it has been shown that the strength at a true strain of 0.2 correlates strongly with the hardness and does not depend on the starting microstructure within the limits studied [225]. Fig. 26shows that the correlation holds irrespective of whether the steel is in its annealed, hot-rolled or normalised condition, for a large variety of alloys included in the analysis.
![\includegraphics[width=0.98\linewidth]{Hurley_1971.eps}](img166.png) |
It has been emphasised that the austenite grain size should be kept small enough to avoid the fracture of untempered, high-carbon martensite [226]; some examples of microcracks are illustrated in as a function of the austenite grain size in a high-carbon steel, Fig. 27. Microcracking of this kind has been reported for 52100 steel quenched after austenitisation at about 1100 ![]() C [226]. Studies on carburised steel have shown that the cracks are known to adversely influence the fatigue properties [227]. Fracture can also occur at the austenite grain boundaries by impingement with large martensite plates [228].
C [226]. Studies on carburised steel have shown that the cracks are known to adversely influence the fatigue properties [227]. Fracture can also occur at the austenite grain boundaries by impingement with large martensite plates [228].
It was at one point argued that such cracking is an artefact associated with plates of martensite in the close proximity of the metallographic sample surface, i.e.,a function of metallographic specimen preparation [229]. Subsequent work, reviewed in [226] indicated that the cracks are indeed a consequence of martensitic transformation rather than a surface effect. Delayed acoustic emission signals after quenching to martensite have been shown to result from cracking, and these presumably arise from the body of the material rather than just the surface [230].
The microcracking has been attributed to impingement between plates of martensite forming on different variants of habit planes in the same austenite grain [231, 232, 233]. Experiments in which the bearing steel is cooled slowly through the martensite transformation temperature range, or cooled through it in a stepwise manner, result in fewer microscopic cracks because the plates that form first acquire a degree of tempering and possibly due to the reduction in quench stresses. Any reduction in cracking due to the tempering of martensite is at first sight surprising since the heat-treatment is an aftermath to the formation of martensite. One reason for the apparent reduction is healing by cementite precipitation at microcracks [234]. There may also be a role of dimensional changes induced in the martensite by tempering, and the associated plasticity, on the reduction in cracking tendency [235].
Marder et al.[231] concluded that the tendency for cracking is not a function of the austenite grain size when the latter is coarser than 100 µm [231], but even more refined austenite grains do reduce the tendency for cracking [232]. Recent work has interpreted this dependence in terms of the ability to transfer load onto the martensite as the composite mixture of ![]() is deformed [236]. The spacing between cracks in long martensite plates corresponds approximately to the stress transfer length of composite theory, and an austenite grain size (and hence martensite plate size) which is finer than this transfer length dramatically reduces microcracking. This may explain the contention that there is a critical
is deformed [236]. The spacing between cracks in long martensite plates corresponds approximately to the stress transfer length of composite theory, and an austenite grain size (and hence martensite plate size) which is finer than this transfer length dramatically reduces microcracking. This may explain the contention that there is a critical ![]() -plate size below which cracking does not occur [237].
-plate size below which cracking does not occur [237].
An increase in the carbon concentration of the martensite can reasonably be expected to enhance cracking, either by inducing a lath to plate martensite morphological transition, or by making the martensite more brittle through hardening or because the lattice becomes more tetragonal [238]. However, when the concentration exceeds about ![]() wt%, there is a transition in the habit plane of martensite from
wt%, there is a transition in the habit plane of martensite from ![]() to
to ![]() accompanied by a reduction in cracking [232]. There are multiple explanations for this, based for example on the change in angle of impingement between colliding plates, or the sequence in which successive plates form.
accompanied by a reduction in cracking [232]. There are multiple explanations for this, based for example on the change in angle of impingement between colliding plates, or the sequence in which successive plates form.
|
(a)
![\includegraphics[width=0.45\textwidth]{1200etched.eps}](img171.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{1200unetched.eps}](img172.png) (a) ![\includegraphics[width=0.45\textwidth]{1000etched.eps}](img173.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{1000unetched.eps}](img174.png)
|
Steels supplied to the bearing manufacturer for making raceways are in the form of tubes or forgings whereas the rolling elements are made by cold-forging drawn, spheroidised-annealed wire. The aim of spheroidise annealing is to facilitate machining, and warm- and cold-forming operations, by inducing a microstructure which is a mixture of relatively coarse cementite particles and ferrite. The roughness of machined surfaces is also reduced in the process [239]. Reasonably large cementite particles and a small number density is conducive to less wear on the tools used for machining, lamellar carbides of the type associated with incomplete spheroidisation lead to enhanced tool-degradation [240]. A consistent spheroidise-annealed microstructure results in a reproducible volume change during heat treatment, optimised machining allowances and reduced costs.
Spheroidisation reduces the hardness of the steel supplied to a bearing manufacturer to about 230HV [241]. The yield and ultimate tensile strengths for 52100 steel in this condition are 455 and 635 MPa respectively, with an elongation of 36% [187]; the yield here presumably corresponds to a 0.2% proof stress. Comprehensive data for the spheroidised state are presented in Fig. 28, but it is worthy of note that the strength can vary significantly as a function of position because of chemical differences caused by segregation during casting [242].
Recent work has shown that the hardness is not sensitive to the substitutional solute content [243]. On the other hand, the kinetics of spheroidisation have long been known to depend both on the chromium and carbon concentrations. A higher carbon concentration promotes spheroidisation, apparently by providing a greater initial number density of nucleation sites, and the action of chromium manifests by reducing the interlamellar spacing of pearlite< /a>, which is often the starting structure for a spheroidising anneal [52, 51]. Attempts to reduce the carbon concentration of 52100 in order to avoid undissolved cementite have had limited success because of the inability of the hypereutectoid steel to be readily spheroidised [52].
![\includegraphics[width=0.98\linewidth]{Lowisch_2006.eps}](img175.png) |
There are two essential methods for soft-annealing of the 52100 steel type steels, the first involving continuous spheroidisation during cooling from the partially austenitic ![]() Condition, and the other utilising isothermal annealing at a temperature which is less than that at which austenite begins to form, Fig. 30a. The former method is more suited to hypereutectoid steels because it reduces the proeutectoid cementite layers at the prior austenite grain boundaries into spheres, and subcritical annealing to hypoeutectoid alloys where it is said to be more rapid [245]. Finer microstructures in general tend to spheroidise more rapidly during subcritical annealing [246]; this might be expected since the process is driven by the minimisation of total interfacial area per unit volume. In some cases the steel is first heat-treated to produce the finest possible pearlite< /a> to permit more rapid dissolution of the carbides during the spheroidising heat treatment [247]; it has been demonstrated for 52100 type steel that fine, lamellar pearlite< /a> dissolves at a greater rate than spheroidised cementite of the type often present in the steel supplied to the bearing manufacturer [248]. More complex but possibly less practical processes can involve thermal cycling about the eutectoid temperature [249, 250].
Condition, and the other utilising isothermal annealing at a temperature which is less than that at which austenite begins to form, Fig. 30a. The former method is more suited to hypereutectoid steels because it reduces the proeutectoid cementite layers at the prior austenite grain boundaries into spheres, and subcritical annealing to hypoeutectoid alloys where it is said to be more rapid [245]. Finer microstructures in general tend to spheroidise more rapidly during subcritical annealing [246]; this might be expected since the process is driven by the minimisation of total interfacial area per unit volume. In some cases the steel is first heat-treated to produce the finest possible pearlite< /a> to permit more rapid dissolution of the carbides during the spheroidising heat treatment [247]; it has been demonstrated for 52100 type steel that fine, lamellar pearlite< /a> dissolves at a greater rate than spheroidised cementite of the type often present in the steel supplied to the bearing manufacturer [248]. More complex but possibly less practical processes can involve thermal cycling about the eutectoid temperature [249, 250].
The details of the microstructure in either the soft-annealed or any other structural state influences the properties obtained following the subsequent hardening heat treatment. The kinetics of austenitisation are sensitive to the initial shape and size of ferrite grains and cementite particles [251]. The size of the austenite grains and hence the size distribution of subsequent martensite, and the dissolution rates of the carbides (related the composition of martensite) have been shown to depend on the initial structure [252].
When the starting microstructure is pearlitic following hot-rolling (Fig. 3) with a hardness of about 340HV [241], it takes many hours of isothermal heat-treatment to achieve the required degree of spheroidisation, during which the steel must be protected against decarburisation, for example, by using a controlled furnace-atmosphere containing a few percent of hydrogen and carbon monoxide [247, 253, 254]. One purpose of continuous annealing of the type illustrated in Fig. 30is to avoid the formation of lamellar pearlite< /a>. When the steel is heated into the two-phase ![]() phase field, the presence of sufficient cementite particles can prevent the onset of pearlite< /a>. This is because the existing cementite particles absorb the carbon that is partitioned at the
phase field, the presence of sufficient cementite particles can prevent the onset of pearlite< /a>. This is because the existing cementite particles absorb the carbon that is partitioned at the ![]() transformation front in a process referred to as the `divorced eutectoid transformation', which does not rely on the cooperative growth of ferrite and cementite [255]. The concept of divorced pearlite< /a> has been known for a long time [256, 257, 259, 258] as has its role in generating the spheroidised state during continuous cooling [260, 246] or through heat treatment [261]. It was known as early as 1920 [256] that the presence of carbide particles in hypereutectoid steels led to the formation of globular pearlite< /a>, in which the cementite phase is spheroidised during transformation, as illustrated in Fig. 29. A secondary effect is that this kind of divorced pearlite< /a> forms at a higher temperature during continuous cooling than lamellar pearlite< /a> [257]; this is because the latter requires the nucleation of cementite and the establishment of cooperative growth with ferrite in order to form.
transformation front in a process referred to as the `divorced eutectoid transformation', which does not rely on the cooperative growth of ferrite and cementite [255]. The concept of divorced pearlite< /a> has been known for a long time [256, 257, 259, 258] as has its role in generating the spheroidised state during continuous cooling [260, 246] or through heat treatment [261]. It was known as early as 1920 [256] that the presence of carbide particles in hypereutectoid steels led to the formation of globular pearlite< /a>, in which the cementite phase is spheroidised during transformation, as illustrated in Fig. 29. A secondary effect is that this kind of divorced pearlite< /a> forms at a higher temperature during continuous cooling than lamellar pearlite< /a> [257]; this is because the latter requires the nucleation of cementite and the establishment of cooperative growth with ferrite in order to form.
|
(a)
![\includegraphics[width=4.5cm]{www.phase-trans.msm.cam.ac.ukley_1.eps}](img177.png) (b) (b) ![\includegraphics[width=4.5cm]{www.phase-trans.msm.cam.ac.ukley_2.eps}](img178.png)
|
However, the detailed mechanism began to be actively discussed more recently [255, 262] and is illustrated schematically in Fig. 31a, and Verhoeven has presented a quantitative model based on diffusion-controlled growth which is summarised here. During the transformation when the mixture of austenite and cementite is supercooled below ![]() fluxes are created towards cementite particles in both the austenite and ferrite, as illustrated in Fig. 31b. If the
fluxes are created towards cementite particles in both the austenite and ferrite, as illustrated in Fig. 31b. If the ![]() interface advances at a velocity
interface advances at a velocity ![]() , then the amount of carbon partitioned must equal that absorbed in the cementite if equilibrium is to be maintained at the interfaces concerned:
, then the amount of carbon partitioned must equal that absorbed in the cementite if equilibrium is to be maintained at the interfaces concerned:
The model [262] has been used to reasonable effect to explain the influence of chromium and manganese concentrations, on the spheroidisation of an otherwise 52100 steel type steel, taking into account the change in equilibrium concentrations due to the substitutional solutes [243]. Unfortunately, the conclusions regarding a transition from divorced to lamellar pearlite< /a> are doubtful because no account was taken of the influence of Mn or Cr on the growth rate of lamellar pearlite< /a>; these elements have a strong effect on pearlite< /a> kinetics [266]. The influence of solutes in general, on spheroidisation and divorced pearlite< /a> is only partly understood. For example, small concentrations (0.03 wt%) of hafnium promote the formation of divorced pearlite< /a> [258] but the mechanism has not been investigated. A large phosphorus concentration is known to retard spheroidisation but again, the mechanism is not clear [267]; the growth rate of cementite allotriomorphs at austenite grain boundaries does not depend on the phosphorus concentration of the steel [268]. Silicon has been shown experimentally to retard the spheroidisation process, probably because phase diagram calculations indicate that the solubility of carbon in austenite decreases [270, 269]. This simple interpretation would lead not only to a greater fraction of cementite, but should also diminish any concentration gradients due to capillarity effects within the austenite between coarse and fine particles, thereby providing a second mechanism for the retardation of coarsening. However, qualitative interpretations [269] based on the influence of silicon on the activity and chemical potential of carbon in the austenite are weak; for example, Fig. 8b of [269] identifies the chemical potential of carbon in cementite to be different from that in austenite, which is not correct given that there is an equilibrium between the two phases.
In an interesting study, induction annealing was used to produce divorced pearlite< /a>, i.e.spheroidised cementite in a matter of minutes [271]. Undissolved cementite was preserved by rapid austenitisation of a 52100 type steel for 30s at 850 ![]() C. This was then transformed isothermally at 650
C. This was then transformed isothermally at 650 ![]() C for 17min to produce the required microstructure with a hardness of about 235HV.
C for 17min to produce the required microstructure with a hardness of about 235HV.
![\includegraphics[width=0.98\linewidth]{spheroidise.eps}](img190.png) |
|
(a)
![\includegraphics[width=0.40\textwidth]{Divorced.eps}](img191.png) (b) (b) ![\includegraphics[width=0.5\textwidth]{Divorced_model.eps}](img192.png)
|
![\includegraphics[width=0.98\linewidth]{Verhoeven_1998.eps}](img193.png) |
The purpose of spheroidisation is to coarsen and hence soften the microstructure, but there are consequences because the total amount of cementite is of the order of 15vol.% in the 52100 type bearing steels, Fig. 4. The particles in the spheroidised condition have a size in the range 0.5-3 µm (the ferrite grain size in the range 15-25 µm [273]). The size of the carbides can be controlled using spheroidising anneals, followed by the usual quench and temper heat-treatments. Using the method, it has been demonstrated that there is an advantage from a fatigue point of view in having a fine dispersion in the soft-annealed condition, so that the carbides which are undissolved during austenitisation can also be small in size [274, 43]. There is another reason in favour of the refined cementite particles; the spheroidised steel is ring-rolled, i.e. cold-deformed into a ring form, during which much of the deformation is in the majority ferrite phase with the much harder cementite particles behaving relatively rigidly [273]. The resultant mismatch of strain between the two phases leads to the opening up of voids at the interfaces between the larger cementite particles and the matrix, Fig. 33. Similar voids are found at the ends of the larger (primary) alloy-carbides in processed M50 steel (Table 8) [275]. If these are not healed in continued or subsequent processing then the voids or weakened interfaces must contribute to the initiation of fatigue damage and is one explanation why the refinement of grain size in M50 does not contribute to improved rolling contact fatigue performance [276].
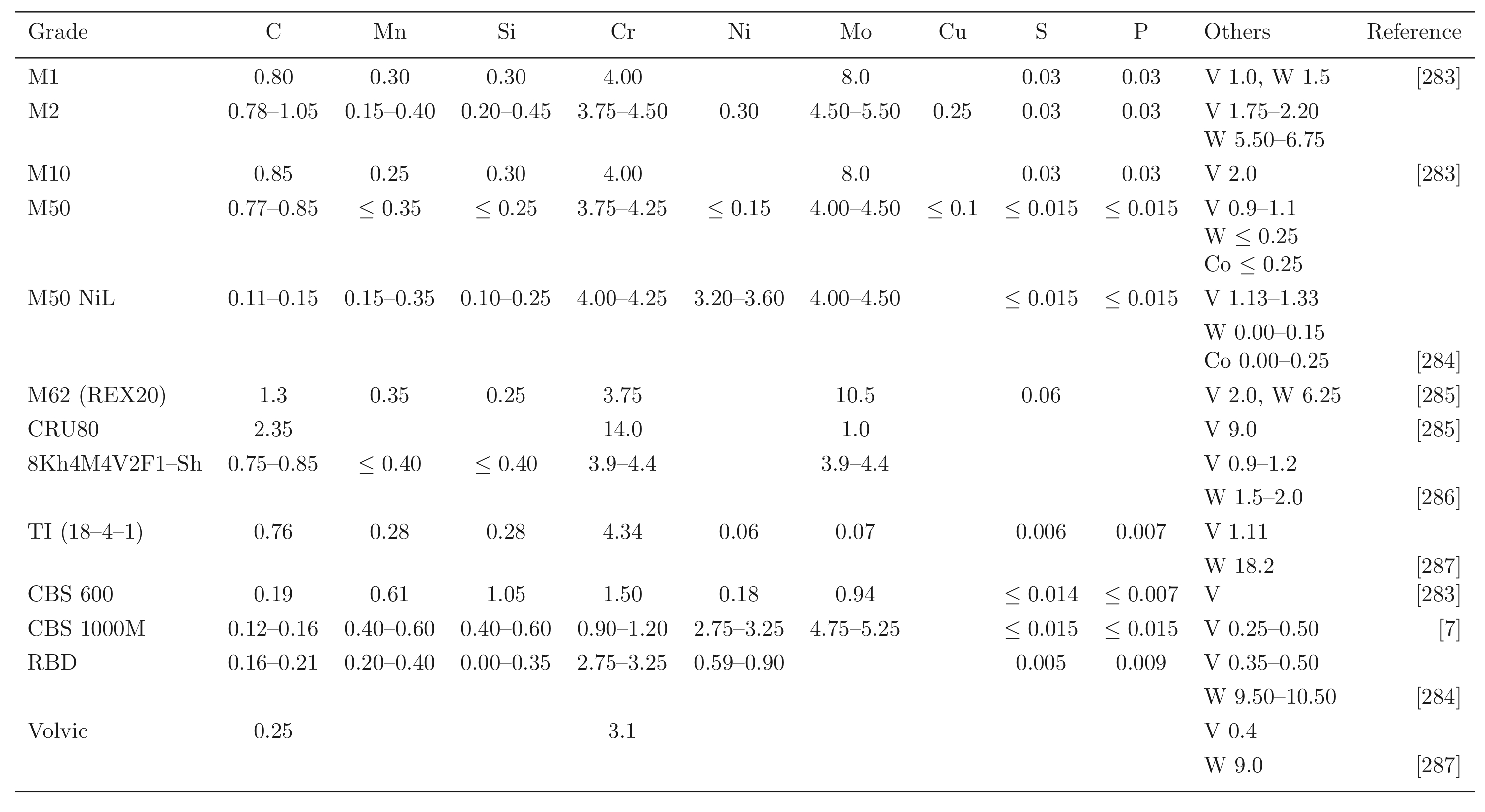 |
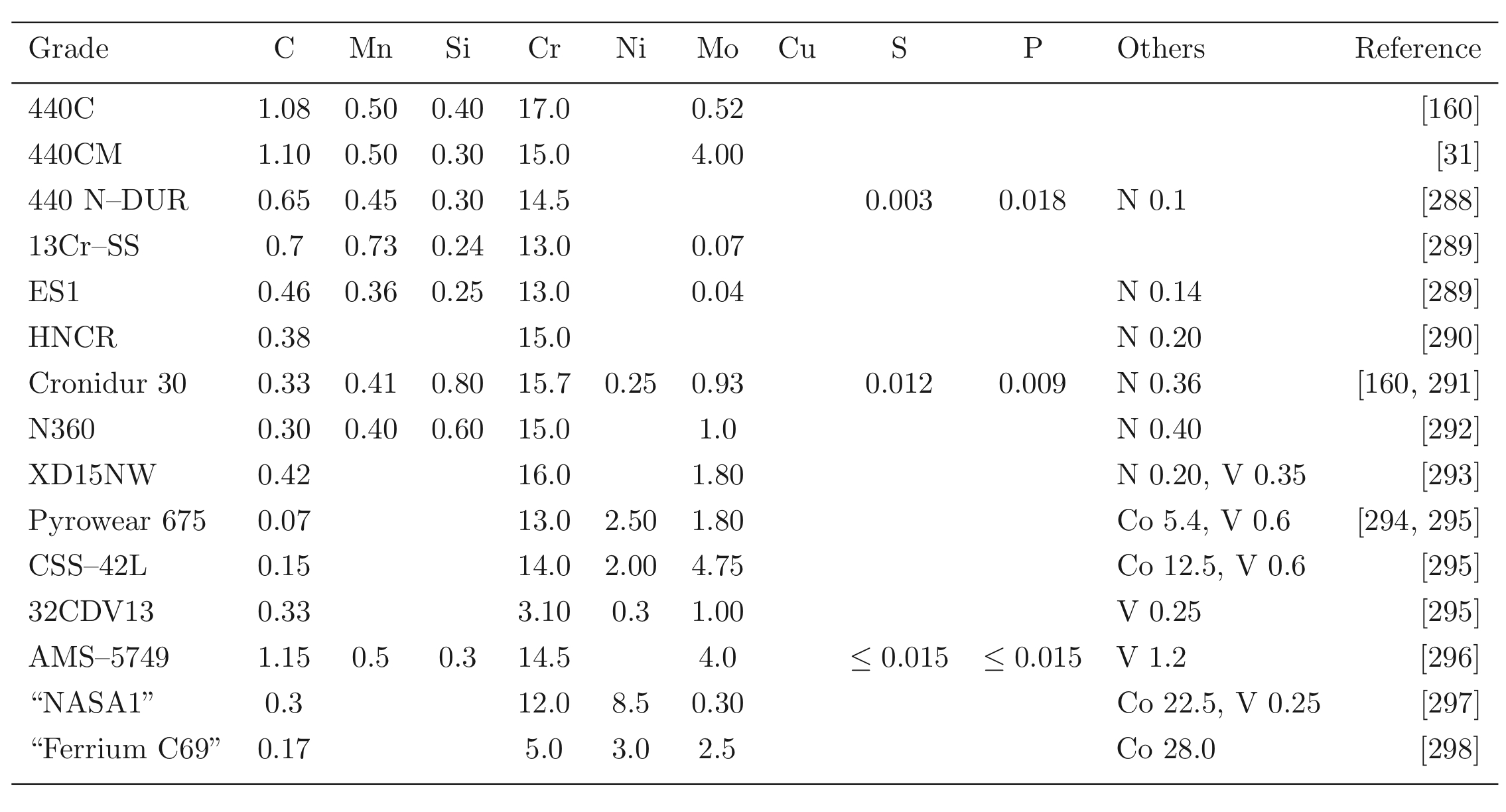 |
![\includegraphics[width=0.98\linewidth]{Ryttberg_2010.eps}](img194.png) |
It is important in alloy development programmes to appreciate that graphite is generally more stable than cementite, but is usually not observed because cementite is kinetically favoured. However, spheroidisation heat treatments can be prolonged, and graphite formation has been observed in chromium-free steels containing a relatively large concentration of silicon (0.7 wt%), [278, 277]. Silicon has a very low solubility in cementite and hence promotes graphitisation.
The structure of the steel prior to spheroidisation can be problematic for large section hot-rolled bars, which develop networks of carbides along the austenite grain boundaries in the central regions which cool relatively slowly. These network-carbides are more difficult to anneal and the problem can be mitigated by cooling more rapidly from the hot-rolling temperature [279]. Alternatively, normalising the hot-rolled steel prior to the spheroidising heat treatment has also been reported to help mitigate carbide clusters in the final microstructure [280]. Repeat annealing with a second tempering treatment at a lower temperature is said to help break up the networks [281].
Aircraft engines represent one of the most sophisticated of engineering technologies; it is not surprising that they have led the development of some quite elaborate steels. Bearings on engine shafts have to tolerate vibratory stresses, bending moments and high rotation speeds, for example, 25,000 revolutions per minute, elevated temperatures and aggressive lubrication 10 . The fracture of a bearing race can have serious consequences on the integrity of the engine [283].
The thrust to weight ratio has to be maximised in order to optimise fuel efficiency. One way of achieving this is to reduce the mass of bearings, as long as the steel used in their manufacture is able to bear the resulting increase in structural stresses [300]. Whereas in slowly rotating bearings it is the highly-stressed inner race which determines the fatigue life of the bearing, centrifugal forces accompanying high-speed rotation add to the applied loads; the contact stresses on the outer race can then reach some 2GPa [301]. Aircraft bearings have outer to inner diameter ratios of about 1.1 so that they can be approximated as thin rings for the calculation of the hoop stress which is given by ![]() where
where ![]() is the density,
is the density, ![]() the average ring radius and
the average ring radius and ![]() the angular speed of the shaft in radians per second [300]. The distance travelled by a point on the bearing raceway per minute is of the order of 3000mmin
the angular speed of the shaft in radians per second [300]. The distance travelled by a point on the bearing raceway per minute is of the order of 3000mmin ![]() , for a raceway circumference of 0.12m. 11 This typically leads to a centrifugal hoop stress in excess of 200 MPa.
, for a raceway circumference of 0.12m. 11 This typically leads to a centrifugal hoop stress in excess of 200 MPa.
It frequently is necessary to sustain combined radial and thrust loads; some illustrative data are listed in Table 9. Given these circumstances, the bearing inner ring is often press-fitted to the shaft in order to prevent relative rotation and consequent fretting or ordinary wear. This fitting adds to the hoop stresses on the ring; it is recommended that this component of the hoop stress should not exceed about 140 MPa [302].
| % of speed | % time | Thrust / N | Life / h | Maximum Hertz stress / MPa | |
| Inner ring | Outer ring | ||||
| 60 | 10 (idle) | 3114 | 1048 | 1331 | |
| 100 | 20 (take off) | 11121 | 1572 | 1944 | |
| 100 | 70 (cruise) | 6672 | 1331 | 1855 | |
One of the distinctions of steels destined for aerospace applications or arduous environments, is that they retain their hardness at temperatures in the range 120-320 ![]() C [305, 304], Fig. 37. Strength at high temperatures can also be useful in temporarily maintaining bearing integrity in circumstances where lubrication fails or becomes marginal [307, 306]. Hardness values below 58 HRC are undesirable as the usual steels then suffer from `brinelling', i.e.,the formation of grooves on the raceways. Early attempts at appropriate steel design were based on low-alloy steels modified in order to increase their temper resistance by boosting the silicon or aluminium concentrations, and introducing molybdenum carbides; Crucible Steel's vacuum-melted alloy 52CB (Table 1) is an example of this with the composition also designed to eliminate retained austenite in order to maintain dimensional stability [33, 308]. However, the best elevated temperature performance was obtained from adaptations of richly-alloyed tool steels such as M50; some typical chemical compositions are listed in Table 8. The cleanliness of aerospace bearing steels is all important and it is well-known that the fatigue life is enhanced by double vacuum melting, i.e.,vacuum induction melting and vacuum arc remelting [9]. In this latter process the material is made an electrode from which an arc is generated, which causes droplets of the metal to trickle through the vacuum and become purified. The molten metal is usually contained by a water-cooled mould and solid impurities have an opportunity to separate by floatation. The controlled solidification inherent in vacuum arc remelting results in a macroscopically uniform ingot which few solidification defects [133].
C [305, 304], Fig. 37. Strength at high temperatures can also be useful in temporarily maintaining bearing integrity in circumstances where lubrication fails or becomes marginal [307, 306]. Hardness values below 58 HRC are undesirable as the usual steels then suffer from `brinelling', i.e.,the formation of grooves on the raceways. Early attempts at appropriate steel design were based on low-alloy steels modified in order to increase their temper resistance by boosting the silicon or aluminium concentrations, and introducing molybdenum carbides; Crucible Steel's vacuum-melted alloy 52CB (Table 1) is an example of this with the composition also designed to eliminate retained austenite in order to maintain dimensional stability [33, 308]. However, the best elevated temperature performance was obtained from adaptations of richly-alloyed tool steels such as M50; some typical chemical compositions are listed in Table 8. The cleanliness of aerospace bearing steels is all important and it is well-known that the fatigue life is enhanced by double vacuum melting, i.e.,vacuum induction melting and vacuum arc remelting [9]. In this latter process the material is made an electrode from which an arc is generated, which causes droplets of the metal to trickle through the vacuum and become purified. The molten metal is usually contained by a water-cooled mould and solid impurities have an opportunity to separate by floatation. The controlled solidification inherent in vacuum arc remelting results in a macroscopically uniform ingot which few solidification defects [133].
M50 is a high-hardenability steel (Fig. 34) quenched to produce a predominantly martensitic microstructure. It relies on molybdenum carbides for its hot hardness, and is the most common alloy for the manufacture of turbine engines. They can be particularly susceptible to decarburisation and hence must be protected during heat treatment. The steel is usually preheated to 500 ![]() C, held there and then heated to 800
C, held there and then heated to 800 ![]() C, followed by austenitisation at 1100
C, followed by austenitisation at 1100 ![]() C for long enough to reach temperature. During this austenitisation, approximately 3-4 wt% of molybdenum-rich
C for long enough to reach temperature. During this austenitisation, approximately 3-4 wt% of molybdenum-rich ![]() , vanadium-rich MC and possibly chromium-rich
, vanadium-rich MC and possibly chromium-rich ![]() are not dissolved [309], Fig. 35. The steel is then quenched to 560
are not dissolved [309], Fig. 35. The steel is then quenched to 560 ![]() C and air-cooled, leading to a microstructure consisting of undissolved carbides, martensite and about 20-30% retained austenite. A sub-zero soak at about
C and air-cooled, leading to a microstructure consisting of undissolved carbides, martensite and about 20-30% retained austenite. A sub-zero soak at about ![]() C is used to reduce the retained austenite content. Secondary hardening is conducted by tempering at 540-550
C is used to reduce the retained austenite content. Secondary hardening is conducted by tempering at 540-550 ![]() C for 2h followed by air-cooling to ambient temperature. Tests indicate that the sub-zero treatment does not significantly influence fatigue life [282], which mostly scales with the hardness. When the sub-zero treatment is omitted, the alloy might be subjected repeatedly to the
C for 2h followed by air-cooling to ambient temperature. Tests indicate that the sub-zero treatment does not significantly influence fatigue life [282], which mostly scales with the hardness. When the sub-zero treatment is omitted, the alloy might be subjected repeatedly to the ![]() C tempering, with cooling to room temperature between the tempering treatments, in order to minimise the retained austenite content to less than 4% thus improving dimensional stability during service, and in order to enhance toughness [310] 12 .
C tempering, with cooling to room temperature between the tempering treatments, in order to minimise the retained austenite content to less than 4% thus improving dimensional stability during service, and in order to enhance toughness [310] 12 .
The maximum temperature at which 52100 steel can be used continuously is about 160 ![]() C, whereas M50 is designed for temperatures as high at 310
C, whereas M50 is designed for temperatures as high at 310 ![]() C, as is apparent from the hot-hardness data presented in Fig. 37. The hardness is a key factor which limits the operating temperature; it is known even for ambient temperature operation that the contact fatigue life improves as the hardness is increased beyond 54 HRC [311], and M50 is usually through-hardened to at lease 58 HRC [302]. It has been pointed out that even if the hardness remains satisfactory above 400
C, as is apparent from the hot-hardness data presented in Fig. 37. The hardness is a key factor which limits the operating temperature; it is known even for ambient temperature operation that the contact fatigue life improves as the hardness is increased beyond 54 HRC [311], and M50 is usually through-hardened to at lease 58 HRC [302]. It has been pointed out that even if the hardness remains satisfactory above 400 ![]() C, the oxidation resistance of M1, M2, M10 and M50 steels is marginal [312]. The temperature dependence of the hot-strength of a series of secondary-hardening bearing steels (M1, M50, Halmo, WB49) can be normalised as follows [313]:
C, the oxidation resistance of M1, M2, M10 and M50 steels is marginal [312]. The temperature dependence of the hot-strength of a series of secondary-hardening bearing steels (M1, M50, Halmo, WB49) can be normalised as follows [313]:
M50 is sometimes even used when the service temperature is less than 150 ![]() C because of its high rolling contact fatigue life [314], although tests done with
C because of its high rolling contact fatigue life [314], although tests done with ![]() GPa at 66
GPa at 66 ![]() C indicate that 52100 is significantly better in its ability to resist this kind of loading. Furthermore, the M series of steels are more difficult to grind and finish [312]. In general, 52100 is regarded to be superior for applications at relatively low temperatures.
C indicate that 52100 is significantly better in its ability to resist this kind of loading. Furthermore, the M series of steels are more difficult to grind and finish [312]. In general, 52100 is regarded to be superior for applications at relatively low temperatures.
![\includegraphics[width=0.98\linewidth]{TTT_Kline.eps}](img212.png) |
|
(a)
![\includegraphics[width=0.45\textwidth]{Bridge_1971.eps}](img213.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Bridge_1971_2.eps}](img214.png)
|
Most of the through-hardening steels used for aeroengine bearings are derivatives of tool steels and contain relatively large concentrations of solutes. They are not particularly ductile, with little elongation in tension tests, and a fracture toughness in the range 20-30 ![]() [287], Table 10. For this reason the M50 and 52100 steels are not used in tapered roller bearings which not only support greater loads but may require interference fits with shafts, a process which introduces tensile hoop stresses in the ring [1] and increases the chances of catastrophic raceway failure [316]. Thus, in the absence of the hoop stress, failure occurs by spalling, but otherwise the spalling is accompanied by ring failure [317]. The hoop stress
[287], Table 10. For this reason the M50 and 52100 steels are not used in tapered roller bearings which not only support greater loads but may require interference fits with shafts, a process which introduces tensile hoop stresses in the ring [1] and increases the chances of catastrophic raceway failure [316]. Thus, in the absence of the hoop stress, failure occurs by spalling, but otherwise the spalling is accompanied by ring failure [317]. The hoop stress ![]() due to press-fitting is given by [317]:
due to press-fitting is given by [317]:
![\begin{displaymath} \sigma_h\propto \frac{E\Delta r_i}{r_o^2-r_i^2}\biggl[1 - \biggl(\frac{r_o^2}{r^2}\biggr)^2\biggr] \end{displaymath}](img217.png) |
(8) |
T1 (18-4-1) is tungsten-rich, used originally in the Britain in the electroslag refined condition for gas turbine engine mainshaft bearings, hardened to some 60-65 HRC [318]. Following heat treatment, the composition of the matrix is not much different from that of M50 except that tungsten substitutes for molybdenum 13 . Its retained austenite content at about 10% following air-cooling is about a third that of M50, but has a much larger quantity of undissolved carbides (15%) in the form of ![]() . Nevertheless, the general properties of T1 and M50 are very similar, dependent mostly on the matrix ductility and composition [319].
. Nevertheless, the general properties of T1 and M50 are very similar, dependent mostly on the matrix ductility and composition [319].
The large solute content of alloys such as M50 and T1 makes them susceptible to chemical segregation during manufacture. During freezing to an ingot, the regions to solidify last are enriched in carbon and substitutional solutes which have a strong affinity for carbon [315]. As a consequence, large eutectic primary-carbides form, which although they are reduced in size by mechanical working, the fragments remain coarse. The final material contains a bimodal distribution of particles, the finer ones precipitated during tempering and the coarse carbides which are remnants of the solidification process (Fig. 36). The latter influence the development of fatigue damage and are detrimental to formability which is important during the fabrication of bearing rings. One approach is to reduce the total content of carbides without compromising other properties [286].
An alternative method studied in the context of M50 steel is to refine the dispersions by ausforming [320], in which the steel is deformed in its metastable-austenitic state at relatively low temperatures around 600 ![]() C [321, 322, 1]. This requires the time-temperature transformation diagram of the steel to have a bay at the temperature concerned, between the high-temperature diffusional transformations such as pearlite< /a>, and the low temperature displacive transformations such as bainite. As can be seen from Fig. 14steel 52100 steel is not suitable for ausforming whereas Fig. 34shows the sluggish rate of transformation in M50 at the ausforming temperature. Extensive experiments [321, 322] prove that ausformed M50 shows a significant improvement in rolling contact fatigue life as a consequence of the fragmentation and refinement of large carbides. However, ausforming is not in general practicable or cost-effective [9] and can lead to other difficulties by introducing structural defects during the warm-deformation.
C [321, 322, 1]. This requires the time-temperature transformation diagram of the steel to have a bay at the temperature concerned, between the high-temperature diffusional transformations such as pearlite< /a>, and the low temperature displacive transformations such as bainite. As can be seen from Fig. 14steel 52100 steel is not suitable for ausforming whereas Fig. 34shows the sluggish rate of transformation in M50 at the ausforming temperature. Extensive experiments [321, 322] prove that ausformed M50 shows a significant improvement in rolling contact fatigue life as a consequence of the fragmentation and refinement of large carbides. However, ausforming is not in general practicable or cost-effective [9] and can lead to other difficulties by introducing structural defects during the warm-deformation.
![\includegraphics[width=0.98\linewidth]{Kline_1978.eps}](img222.png) |
| % elongation | % reduction of area | ||||
| M50 | 17-20 | 2110 | 2600 | 5 | 10 |
| M50 NiL | 55 | 1175 | 1387 | 15 | 74 |
| RBD | 25 | 1125 | 1410 | 16 | 52 |
| T1 (18-4-1) | 20-22 | 2100 | 2500 |
| Austenitisation | Tempering | ||||
| M50 NiL | 1050 |
1220 | 1363 | ||
| M50 NiL | 1070 |
1202 | 1391 | ||
| M50 NiL | 1070 |
1173 | 1446 | ||
| M50 NiL | 1070 |
1202 | 1391 | ||
| M50 NiL | 1070 |
1207 | 1353 | ||
| M50 NiL | 1090 |
1206 | 1388 | ||
| M50 NiL | 1060 |
61 | |||
| M50 NiL | 1080 |
54 | |||
| M50 NiL | 1080 |
58 | |||
| M50 NiL | 1080 |
60 | |||
| M50 NiL | 1100 |
57 |
![\includegraphics[width=0.8\textwidth]{Bohmer_hardness.eps}](img230.png)
|
M50 NiL was developed in order to satisfy increasing demands for the structural integrity of aeroengine shaft bearings, as a derivative of M50 [325, 162]. With a composite microstructure in which the case-hardened surface is tenacious but the lower-carbon core is not, it is capable of supporting more arduous engine conditions than envisaged for M50. The core toughness is about 40-55 ![]() [324, 284] because the reduced carbon concentration leads to a better distribution of carbide particles, Fig. 38. The nickel is needed to stabilise the austenite [283]. Its hot-strength (Fig. 37) relies on secondary hardening with alloy carbides, mainly
[324, 284] because the reduced carbon concentration leads to a better distribution of carbide particles, Fig. 38. The nickel is needed to stabilise the austenite [283]. Its hot-strength (Fig. 37) relies on secondary hardening with alloy carbides, mainly ![]() ,
, ![]() and MC [326]. The last two of these carbides may remain partially undissolved during the austenitisation heat-treatment.
and MC [326]. The last two of these carbides may remain partially undissolved during the austenitisation heat-treatment.
The relatively soft core does not have sufficient hardness to resist the required contact stresses, so it is fortunate that M50 NiL can be carburised readily in a process which is relatively insensitive to variations in the processing times and temperatures. The carburised region naturally has a larger fraction of carbides and ![]() and possibly
and possibly ![]() are found in addition to the carbides present in the heat-treated core [326]. Case-hardening leads to a favourable compressive stress on the surface, which gives M50 NiL bearings a greater rolling contact fatigue life than those which are made from through-hardened M50. This state of stress in case-hardened structures also enhances the resistance to surface distress resulting from unintended metal-to-metal contact. Early attempts at making a carburisable version of M50 reduced the carbon concentration to about 0.35 wt% [327] but M50 NiL contains even less carbon in order to reduce the hardness of the core. The heat-treatment of case-carburised M50 NiL is similar to that of M50, and after multiple tempering the case contains only about 3% of retained austenite [314]. The carbides within the core of M50 NiL are less than 1 µm in size whereas they can be many tens of micrometres large in M50 [314].
are found in addition to the carbides present in the heat-treated core [326]. Case-hardening leads to a favourable compressive stress on the surface, which gives M50 NiL bearings a greater rolling contact fatigue life than those which are made from through-hardened M50. This state of stress in case-hardened structures also enhances the resistance to surface distress resulting from unintended metal-to-metal contact. Early attempts at making a carburisable version of M50 reduced the carbon concentration to about 0.35 wt% [327] but M50 NiL contains even less carbon in order to reduce the hardness of the core. The heat-treatment of case-carburised M50 NiL is similar to that of M50, and after multiple tempering the case contains only about 3% of retained austenite [314]. The carbides within the core of M50 NiL are less than 1 µm in size whereas they can be many tens of micrometres large in M50 [314].
The alloy designated RBD was developed in the U.K. for military purposes and is a carburising steel with a slightly higher carbon concentration than M50 NiL. In general, the carbide dispersions in M50 Nil are finer than RBD [284] and this gives the former a greater toughness. Both alloys are typically carburised in the range 840-950 ![]() C for periods of 4-30h [163].
C for periods of 4-30h [163].
|
(a)
![\includegraphics[width=0.50\textwidth]{Hetzner_M50NiL.eps}](img234.png) (b) (b) ![\includegraphics[width=0.40\textwidth]{carburise.eps}](img235.png)
|
An alternative approach to obtaining a temperature capability of carburising steel is to retard the martensite tempering reaction, particularly with the addition of silicon [283]. It has long been known that silicon inhibits the precipitation of cementite; concentrations of about 2 wt% silicon can change a brittle, cementite-rich www.phase-trans.msm.cam.ac.uk cast-iron into a ductile graphite-rich grey cast-iron [331]. In strong steels, the silicon is used to control the tempering of martensite [78, 332, 74, 76, 77, 333, 334]. Indeed, this is the basis of the successful alloy 300M used for aircraft undercarriages, containing about 1.6 wt.% Si; in this case the rate at which cementite precipitates from supersaturated martensite is significantly reduced when compared with a corresponding steel without the silicon [335]. The mechanism by which silicon retards the precipitation of cementite is that the driving force for precipitation is dramatically reduced when the cementite is forced to inherit the silicon present in the parent phase. Any retardation is therefore prominent for transformations such as martensite which occur at temperatures where atomic mobility is limited [336, 337]. The bearing steel CBS 600 (Table 8) has an exceptionally large silicon concentration which retards the tempering of martensite; this allows the core of a case-hardened bearing made from this material to have sufficient hardness for use up to 315 ![]() C [283].
C [283].
Attempts have been made to use a combination of nitrogen and carbon to modify the surfaces of M50 and M50 NiL whilst in the ferritic state, to improve both the fatigue and lubricated-wear resistance, with tests done at large Hertz pressures ( ![]() GPa) in order to test partial elastohydrodynamic conditions whereby wear becomes significant [338]. The diffusion/reaction process used results in two surface layers, the topmost consisting of a brittle compound with a layer underneath with a diffusion profile of nitrogen in solid solution. The former was found to be detrimental to properties and would need to be removed or minimised prior to service, but the latter led to an increase in surface hardness to values in excess of 66 HRC. It was found possible to enhance fatigue life at the large contact stress when the compound layer was appropriately controlled, and not surprisingly, the wear resistance of M50 NiL also improved significantly relative to the untreated steel. M50 had essentially identical wear resistance in both the treated and untreated states, and this observation was attributed to the large carbides in this alloy [338]. However, this may not be justified because M50 is in any case through hardened to some 60 HRC, which may be sufficient to resist wear. It remains to be demonstrated that the coarser carbides in M50 are important in resisting wear.
GPa) in order to test partial elastohydrodynamic conditions whereby wear becomes significant [338]. The diffusion/reaction process used results in two surface layers, the topmost consisting of a brittle compound with a layer underneath with a diffusion profile of nitrogen in solid solution. The former was found to be detrimental to properties and would need to be removed or minimised prior to service, but the latter led to an increase in surface hardness to values in excess of 66 HRC. It was found possible to enhance fatigue life at the large contact stress when the compound layer was appropriately controlled, and not surprisingly, the wear resistance of M50 NiL also improved significantly relative to the untreated steel. M50 had essentially identical wear resistance in both the treated and untreated states, and this observation was attributed to the large carbides in this alloy [338]. However, this may not be justified because M50 is in any case through hardened to some 60 HRC, which may be sufficient to resist wear. It remains to be demonstrated that the coarser carbides in M50 are important in resisting wear.
Nitrided M50 has been reported to reach hardness levels of 72 HRC and when subjected to rolling contact stress in excess of 5GPa, cracking was observed on the edge of the rolling track [339]. This is because the perimeter of the contact zone is subjected to a tensile stress. This mechanism of cracking is also observed in hybrid bearings where the rolling element is made of a ceramic and subjected to large contact stresses [340]. Tensile stresses have also been used to explain modes other than those typical of mechanisms associated with shear stresses [341].
CBS 1000 has a similar design philosophy to M50-NiL, in that it is used in the case-hardened condition but with the core sufficiently strengthened using secondary hardening. It has a significantly lower concentration of chromium and vanadium (Table 1); both of these solutes are strong carbide formers and at the same time reduce the activity of carbon in austenite, so it is expected that a reduced concentration should permit carbon to penetrate to a relatively greater depth during carburising than M50 NiL. The general influence of chromium on case depth has been known for some time [342]. Fig. 39compares the carbon concentration as a function of depth for M50 NiL and CBS 1000, carburised under identical conditions.
Duplex hardening involves first the normal hardening heat treatment, followed by surface nitriding. The process can be used for secondary hardening steels such as M50 and M50NiL because the nitriding typically has to be conducted at 500 ![]() C for 40-70h and the intention is not to compromise the hardness achieved following the conventional hardening heat-treatment. The surface hardness that can be achieved following nitriding is in the range 1000-1250HV; the hardness obviously declines as a function of depth, but can reach 0.2mm using the salt nitriding process [344]. Large compressive residual stresses peaking at some 1300 MPa at about 0.1-1.3mm below the surface can be achieved as a result of the nitriding process; in Fig. 40, the stress in the close proximity to the surface is influenced by the grinding operation. Some quite remarkable improvements in rolling contact fatigue life have been demonstrated in comparisons with the corresponding steels given just the conventional heat treatments [344]. Significant advantages have been observed when it comes to the operation of bearings in boundary lubrication or contaminated lubrication conditions; damage propagation rates are dramatically reduced [345].
C for 40-70h and the intention is not to compromise the hardness achieved following the conventional hardening heat-treatment. The surface hardness that can be achieved following nitriding is in the range 1000-1250HV; the hardness obviously declines as a function of depth, but can reach 0.2mm using the salt nitriding process [344]. Large compressive residual stresses peaking at some 1300 MPa at about 0.1-1.3mm below the surface can be achieved as a result of the nitriding process; in Fig. 40, the stress in the close proximity to the surface is influenced by the grinding operation. Some quite remarkable improvements in rolling contact fatigue life have been demonstrated in comparisons with the corresponding steels given just the conventional heat treatments [344]. Significant advantages have been observed when it comes to the operation of bearings in boundary lubrication or contaminated lubrication conditions; damage propagation rates are dramatically reduced [345].
![\includegraphics[width=0.98\linewidth]{Streit_2002.eps}](img238.png) |
The heat generated inside the bearing raceway during the operation of a bearing is in the area influenced by the Hertzian contacts and depends on the local values of the friction coefficient and sliding speed. That which is not dissipated in lubricant serves to heat up the raceway [346]. The extent of this temperature rise depends also on the thermophysical properties of the steel, as listed in Table 11. This particular mechanism of heat generation is said to account for about a third of the loss due to the operation of the bearing. For an oil inlet temperature of 70 ![]() C, the increase in the raceway temperature within the contact zone can be some
C, the increase in the raceway temperature within the contact zone can be some ![]() C for operating conditions typical of aeroengine bearings. This leads to a reduction in the rolling contact fatigue resistance which is greater than that expected from the corresponding reduction in hot-hardness [346], presumably because thermal activation accelerates localised damage mechanisms involving microstructural change. One additional consequence of the sliding is that there are localised temperature and pressure spikes created in the lubricant which lead to a decrease in the lubricant film thickness [347] and hence enhance damage through asperity contact.
C for operating conditions typical of aeroengine bearings. This leads to a reduction in the rolling contact fatigue resistance which is greater than that expected from the corresponding reduction in hot-hardness [346], presumably because thermal activation accelerates localised damage mechanisms involving microstructural change. One additional consequence of the sliding is that there are localised temperature and pressure spikes created in the lubricant which lead to a decrease in the lubricant film thickness [347] and hence enhance damage through asperity contact.
| Steel | Temperature | Density | Specific heat | Thermal conductivity |
| kgm |
||||
| M50 | 20 | 7780 | 448.1 | 25.0 |
| 100 | 7759 | 476 | 26.9 | |
| 200 | 7730 | 512 | 28.2 | |
| 300 | 7700 | 550 | 28.7 | |
| 400 | 7667 | 591 | 28.6 | |
| M50NiL | 20 | 7850 | 436 | 19.3 |
| 100 | 7830 | 463 | 21.3 | |
| 200 | 7804 | 500 | 23.2 | |
| 300 | 7776 | 539 | 24.5 | |
| 400 | 7745 | 581 | 25.0 | |
| Cronidur 30 | 20 | 7660 | 455 | 17.0 |
| 100 | 7640 | 487 | 18.8 | |
| 200 | 7612 | 526 | 20.6 | |
| 300 | 7583 | 566 | 21.9 | |
| 400 | 7551 | 605 | 22.4 |
Corrosion can play many roles in the operation of bearings. In ordinary bearings it may manifest locally when components are stationary for long periods, or through contamination of various sorts. Corrosion is a particular issue for naval aircraft engine bearings where corrosion rate of M50 is said to be unsatisfactory [296]. The consequences of corrosion reactions include the generation of hydrogen which penetrates the steel and does harm to its mechanical properties. The discussion of hydrogen is reserved to a later section.
Stainless steel bearings find applications in corrosive environments, such as those which might occur in the aircraft and paper industries, in food processing and in the manufacture of pumping systems. Chromium can make a steel stainless by forming a thin, coherent and electrically insulating film chromium oxide on the surface exposed to air. The concentration of chromium in solid solution must exceed about 12 wt% for this film to regenerate when damaged. Molybdenum helps improve pitting corrosion resistance [348]. Steel 440C (Table 8) is based on this principle with 17 wt% chromium and 0.75 wt% of molybdenum; the carbon concentration is about 1 wt% in order to ensure the hardness necessary for bearing applications, which is in the range 59-61 HRC [349]. Given the combination of carbon and chromium, the alloy contains coarse stringers of eutectic carbides after hot-deformation processing (Fig. 41), a mixture of ![]() and
and ![]() , 10-30 µm in size [328, 350]. The variation in hardness as a function of austenitisation temperature is illustrated in Fig. 42.
, 10-30 µm in size [328, 350]. The variation in hardness as a function of austenitisation temperature is illustrated in Fig. 42.
It is emphasised that the rolling-contact fatigue performance of steels such as 440C is sensitive to the environment they are exposed to. It has been shown, for example, that the service life is reduced by more than an order of magnitude in the presence of high-pressure, moist CO ![]() Contaminated with chloride [351]; surprisingly, the failure mechanism was apparently not different from the ordinary fatigue modes, i.e.,no particular evidence was obtained for stress corrosion or hydrogen embrittlement phenomena. Therefore, the exact mechanism of accelerated fatigue is not established.
Contaminated with chloride [351]; surprisingly, the failure mechanism was apparently not different from the ordinary fatigue modes, i.e.,no particular evidence was obtained for stress corrosion or hydrogen embrittlement phenomena. Therefore, the exact mechanism of accelerated fatigue is not established.
![\includegraphics[width=0.98\linewidth]{Hetzner_440C.eps}](img243.png) |
The question arises as to whether 17 wt% Cr is necessary for passivation since some of this will be tied up in the form of carbides, of which the coarse variety is in general detrimental to fatigue properties [1]. A variety containing only 0.7C-13Cr wt% martensitic steel (13Cr-SS, Table 8) avoids the eutectic carbides and maintains the corrosion resistance. Steel ES1 is a further development based on a combination of carbon and nitrogen, and with an even greater capacity to resist corrosion, partly because of the alloying with nitrogen [289, 350]. The bearing life is also said to be better with ES1 and this is consistent with the observation that coarse carbides in tool steels increase the rate of fatigue crack growth by initiating bursts of failure ahead of the crack tip [287]. Another steel which seems to be based on the same principles is HNCR is also a nitrogen alloyed stainless steel and in the heat-treated condition has a hardness of 58 HRC and is claimed to have a better corrosion resistance than 440C [290].
A variant of 440C has been developed with a reduced reduced carbon and chromium concentration in order to avoid the large carbides whilst maintaining the corrosion resistance; the hardness of this martensitic stainless steel `440 N-DUR' [288] is maintained at 60 HRC by adding about 0.1 wt% nitrogen. This concentration of nitrogen can be achieved without using pressurised casting techniques. One application of this alloy is in the computer industry where the absence of coarse carbides leads to a better surface finish and a reduced level of noise during operation. Steels such as 440C, 440 N-DUR and XD15N can be induction hardened [352].
![\includegraphics[width=0.98\linewidth]{Tanaka_2002.eps}](img244.png) |
Cronidur 30 is a high nitrogen martensitic steel generally used in the through-hardened condition, with outstanding corrosion resistance and a fine, relatively homogeneous microstructure, particularly in the secondary hardened condition [353, 354]; N360 is almost identical steel produced by a different manufacturer [292]. Like M50 NiL, the steel does not suffer from the presence of large carbide particles because of its low carbon concentration. In contrast, M50 and 440C (Fig. 41) both can exhibit cementite particles as large as 60 µm in size [355]. The microstructure is based on a dispersion of fine carbonitrides which are relatively stable, thus permitting prolonged use to temperatures up to 200 ![]() C, although the accumulation of damage at this temperature is not particularly different from that of M50 [291]; it has been shown that the alloy can be used in applications up to 320
C, although the accumulation of damage at this temperature is not particularly different from that of M50 [291]; it has been shown that the alloy can be used in applications up to 320 ![]() C [357, 356]. Its retained austenite content can be as high as 15%, a value which decreases during service to about 8% in the most stressed regions [291]. In its heat-treated condition the steel has a hardness of about 58 HRC,
C [357, 356]. Its retained austenite content can be as high as 15%, a value which decreases during service to about 8% in the most stressed regions [291]. In its heat-treated condition the steel has a hardness of about 58 HRC, ![]() MPa,
MPa, ![]() MPa,
MPa, ![]() %, and a fracture toughness of
%, and a fracture toughness of ![]() [358]. The alloy is found to have a much greater rolling contact fatigue life, both in full and boundary lubrication conditions, than for example M50 steel [355], Fig. 43.
[358]. The alloy is found to have a much greater rolling contact fatigue life, both in full and boundary lubrication conditions, than for example M50 steel [355], Fig. 43.
As pointed out above, Cronidur 30 is designed for through hardening; however, the alloy has been successful in engineering applications where the surface is induction hardened whilst the core is maintained relatively soft (38 HRC) [359]. It is necessary in order to achieve a surface hardness of 60 HRC, to heat-treat the alloy prior to induction hardening so that the coarse chromium-rich carbides are reprecipitated in a finer state whence they can dissolve rapidly during induction heating. Otherwise, the required surface hardness is not achieved. In this surface hardened condition, the core toughness is some 70 MPam ![]() , and a compressive stress is induced in the surface to a depth of about 1.5mm. Given the intrinsic corrosion resistance of the alloy, this represents an impressive set of properties.
, and a compressive stress is induced in the surface to a depth of about 1.5mm. Given the intrinsic corrosion resistance of the alloy, this represents an impressive set of properties.
![\includegraphics[width=0.98\linewidth]{Trojhan_1999.eps}](img250.png) |
Nitrogen has been known for some time to enhance the pitting corrosion resistance of stainless steels [361, 360]; although the mechanism must depend on the details of the corrosive environment, it is thought that the nitrogen helps from inhibiting compounds at the pit sites [362]. To achieve the high nitrogen concentration, Cronidur 30 is produced using a pressurised electroslag remelting process in which electrodes of the appropriate composition are remelted under a pressure of up to 42bars, with silicon nitride added to adjust the nitrogen concentration. The large chromium concentration aids the absorption of nitrogen by reducing its activity in the steel [363].
Another steel somewhat similar to Cronidur 30 and N360, but with a lower nitrogen concentration because it is not produced using the pressurised electroslag process, is XD15NW (Table 8). It is stainless, has excellent salt-spray corrosion resistance and like Cronidur 30, a much more uniform microstructure when compared with alloys such as 440C as illustrated in Fig. 44. Table 12shows how some of the specialist alloys fare in terms of typical property requirements; detailed information can be found in [295].
|
(a)
![\includegraphics[width=0.45\textwidth]{Tronche.eps}](img252.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Cronidur_30.eps}](img253.png)
|
| Type | Designation | Corrosion | Fatigue | Toughness | Wear |
| Through hardened | Cronidur 30 | 1 | 1 | 3 | 2 |
| XD15NW | 1 | 1 | 1 | 3 | |
| Case hardened | Pyrowear 675 | 2 | 3 | 1 | 1 |
| CSS42L | 2 | 2 | 2 | 1 | |
| Nitrided | 32CDV13 | 3 | 2 | 1 | 1 |
Cryogenic bearings are used in the NASA space shuttle and Ariane rocket engines to pump liquid hydrogen fuel. The bearing raceways are made of steel, the rolling elements from silicon nitride, and the cage is made of PTFE impregnated glass fabric; the PTFE also provides some dry lubricant between the rolling elements and raceway [294]. The martensitic stainless steel 440C has in the past been used for the raceways because it is stainless and strong (Table 13). However, the toughness is compromised by the presence of coarse carbides (Fig. 41) and Cronidur 30 or N360 is now the material of choice because of its greater toughness and superior corrosion resistance, although it should be emphasised that the reported corrosion tests are in sulphuric acid or sodium chloride solutions so their significance with respect to cryogenic pumps is not clear. When used in the induction hardened condition, its core fracture toughness is said to be in excess of 50 ![]() .
.
An experimental alloy designated NASA1 (Table 8) based on a low-carbon, secondary hardening system that avoids any carbides which are undissolved at the austenitisation temperature, has a final hardness of some 60 HRC, toughness of 47 ![]() and sufficient stress corrosion crack resistance has been designed for the pumps in the space shuttle [297], but there do not appear to be any data reported on rolling contact fatigue or performance at cryogenic temperatures. Impressive rolling contact data have been reported for a variant (Ferrium C69) [298, 364]. Work has also been done to utilise a modified version of Ferrium C69 in a surface hardened condition [365].
and sufficient stress corrosion crack resistance has been designed for the pumps in the space shuttle [297], but there do not appear to be any data reported on rolling contact fatigue or performance at cryogenic temperatures. Impressive rolling contact data have been reported for a variant (Ferrium C69) [298, 364]. Work has also been done to utilise a modified version of Ferrium C69 in a surface hardened condition [365].
| Elongation / % | Charpy / J | ||||||
| 440C, 58 HRC | Ambient | 2027 | 1273 | 2516 | 1748 | 0.2 | 19 |
| 440C, 58 HRC | 78 | 1127 | 3 | ||||
| Cronidur 30, 58 HRC | Ambient | 1864 | 1862 | 2610 | 2169 | 4 | 120 |
| Cronidur 30, 58 HRC | 78 | 20 | |||||
| Cronidur 30, 34 HRC | 78 | 1346 | 1581 | 4 | |||
Steels produced by a powder metallurgical route can be more richly alloyed than those which are cast, since chemical segregation cannot in the former case extend over distances larger than the powder size. Alloys produced by this more expensive method are usually chosen when a hardness greater than 60 HRC is required, and when the properties can be maintained at higher temperatures and loads. Abrasion resistance, operation in contaminated or corrosive environments, ability to resist shock loading are other possible distinguishing characteristics which can be achieved by manufacturing bearing rings using powder metallurgy [366].
Hybrid bearings in which the rolling elements are made from silicon nitride (Si ![]() N
N ![]() ) which makes them harder than steel balls; the elastic modulus of silicon nitride is also greater, leading to larger contact stresses on steel raceways for a given load. It follows that to achieve the same load-bearing capacity, the steel raceways must have a hardness greater than can be achieved using 52100 steel. M62 (REX20) and CRU80 (Table 8) are two examples of alloys produced using powder metallurgy, both extremely rich in carbon. They are made using gas atomisation, hot isostatic pressing and forging, resulting in a fully dense alloy at the end of the process. CRU80 has a large chromium concentration for improved corrosion resistance and was developed as a potential replacement for 440C [285]. Both are martensitic with finely dispersed alloy-carbides which enhance the wear resistance. After oil quenching from temperatures in the range 1150-1215
) which makes them harder than steel balls; the elastic modulus of silicon nitride is also greater, leading to larger contact stresses on steel raceways for a given load. It follows that to achieve the same load-bearing capacity, the steel raceways must have a hardness greater than can be achieved using 52100 steel. M62 (REX20) and CRU80 (Table 8) are two examples of alloys produced using powder metallurgy, both extremely rich in carbon. They are made using gas atomisation, hot isostatic pressing and forging, resulting in a fully dense alloy at the end of the process. CRU80 has a large chromium concentration for improved corrosion resistance and was developed as a potential replacement for 440C [285]. Both are martensitic with finely dispersed alloy-carbides which enhance the wear resistance. After oil quenching from temperatures in the range 1150-1215 ![]() C, they are repeatedly tempered at 5400-560
C, they are repeatedly tempered at 5400-560 ![]() C for two hours to give a microstructure containing about 20-23vol.% of carbides, some of which are generated by secondary hardening [366, 367]. An intermediate cryogenic treatment may be included to control the quantity of retained austenite to about 5vol.%.
C for two hours to give a microstructure containing about 20-23vol.% of carbides, some of which are generated by secondary hardening [366, 367]. An intermediate cryogenic treatment may be included to control the quantity of retained austenite to about 5vol.%.
REX20 is an air-melted powder metallurgical version of M62 tool steel, and CRU20 is simply the vacuum induction melted variant with a substantially lower sulphur content, which has been shown to have a rolling contact fatigue resistance comparable to that of silicon nitride [368]. It can achieve hardness in the range 66-67 HRC giving it a static stress bearing capacity of 3790-4100 MPa [367]. When applied in hybrid bearings, the fatigue life can be some six times greater than an identically loaded bearing made from 52100 steel [369]; indeed, the life may be determined by the failure of the balls through sintering defects rather than of the raceway.
CRU80 can achieve a hardness in the range 58-62 HRC depending on heat treatment which compares with 58 HRC for 440C wrought-steel, but can be much more corrosion resistant; it has almost twice the carbide content of 440C and hence a better adhesive or mildly-abrasive wear resistance [366].
Conventional cast and wrought bearing steels such as M50 and 440C have been compared against their powder processed variants [370]. The latter do not compete on a cost basis because the fatigue is found to be comparable to that of cast alloys, in spite of the more homogeneous and fine microstructure. It is possible that this could be explained by the much greater oxygen concentration ( ![]() ppmw) of the powder processed alloys. On the other hand, the absence of coarse carbides which originate in long-range chemical segregation results in better surface finish and reduced probability of early failures [370]. Another advantage is that the amount of waste associated with the production of rings by powder metallurgy is reduced relative to the wrought product [371]. The damage mechanism, for example the structural changes in the sub-surface layers (carbide decay and White matter), are essentially identical in roller bearing rings manufactured using powder metallurgy [373, 372]. However, there may be residual porosity from the sintering process and that can be the predominant source for the initiation of butterflies rather than the non-metallic inclusions [373], consistent with early work indicating that voids are more potent sites for butterfly formation [374].
ppmw) of the powder processed alloys. On the other hand, the absence of coarse carbides which originate in long-range chemical segregation results in better surface finish and reduced probability of early failures [370]. Another advantage is that the amount of waste associated with the production of rings by powder metallurgy is reduced relative to the wrought product [371]. The damage mechanism, for example the structural changes in the sub-surface layers (carbide decay and White matter), are essentially identical in roller bearing rings manufactured using powder metallurgy [373, 372]. However, there may be residual porosity from the sintering process and that can be the predominant source for the initiation of butterflies rather than the non-metallic inclusions [373], consistent with early work indicating that voids are more potent sites for butterfly formation [374].
Non-metallic inclusions are of particular importance in the context of steels for bearings. We shall see that refining and melting practice has to be adapted to deal with the so-called endogenous particles which are generated during the deoxidation process, and exogenous inclusions arising from slag entrapment, contamination from refractory materials and oxidation in air when the molten steel is poured without isolation from the environment.
Experiments using radioactive markers indicate that some 70% of the oxide inclusions originate from the vacuum degassing and deoxidation using aluminium, the remainder coming from the furnace slag or reactions within the mould [375, 376]. Aluminium-free deoxidation is usually based on silicon with the resulting silica absorbed into a lime-based slag; the process then includes vacuum treatment to reduce any fine SiO ![]() by the carbon present in the melt [10]. This last step is not possible with alumina given the strong affinity between aluminium and oxygen. There has been an initial study on deoxidation using an Al-Mg alloy, which at the right chemical composition changes the inclusion from alumina to an
by the carbon present in the melt [10]. This last step is not possible with alumina given the strong affinity between aluminium and oxygen. There has been an initial study on deoxidation using an Al-Mg alloy, which at the right chemical composition changes the inclusion from alumina to an ![]() spinel [377]. The spinel particles are reported to be much finer than corresponding alumina particles; the work deserves detailed investigation and characterisation.
spinel [377]. The spinel particles are reported to be much finer than corresponding alumina particles; the work deserves detailed investigation and characterisation.
The history of the manufacture of bearing steels has been summarised by [378] and is illustrated schematically in Fig. 45. In the days when bearing steels were made using air melting, the emphasis was on the type of refractory used, i.e.,whether it is acidic or basic [379, 3]. The term `basic' refers to the fact that the refractories based on magnesite (MgO) or lime (CaO) as opposed to silica which is `acidic'; slags are similarly classified and a basic slag is more conducive to the removal of impurities such as sulphur or phosphorus from the high-carbon steel melts typical in the bearings industry [380]. A basic oxide can react with water to form a base. Steel produced by acid melting has a lower content of nonmetallic inclusions (primarily silicates), with relatively benign shapes and deformability, and there are other advantages reviewed recently [381].
The next stage in obtaining better steel quality was to use selected scarp as the feedstock into electric arc furnaces to further reduce the impurity content when compared with the alloy produced from ore. The scrap, and alloy additions, determine the composition of the melt, which can then be refined to control the phosphorus, nitrogen and sulphur concentrations. The original practice was to complete the liquid steel refining within the furnace itself. However, the introduction of ladle metallurgy led to a step change both in the control of unwanted solutes and phases, and in the entire production chain. Indeed, a point was reached where the melting process (open-hearth, electric arc, basic oxygen furnace) became less important to cleanliness because the inclusion content could be greatly reduced by ladle-treatment and the careful pouring and protection of molten steel at all stages whilst it is exposed to the environment [383, 382].
The essence of ladle metallurgy is that the molten steel is refined in a separate container where the process can be controlled accurately; for example, aluminium, silicon or calcium can be injected into the molten steel to promote deoxidation and desulphurisation [385, 384]. It is known that the majority of alumina based inclusions that are found in bearing steels can be traced to the deoxidation process in the ladle furnace [375]. Argon gas stirring or inductive stirring are therefore used to encourage the alumina inclusions to float out of the melt [386]. The stirring is maintained typically for 20-30min, during which the oxygen content is reduced by the floatation of inclusions from about 12 to 6 ppmw [387]. Inductive stirring is said to be more effective in doing so [120]. Cleanliness during this secondary steel-making process is promoted by the use of a high-alumina ladle lining [389, 388]; this is because in high-alumina bricks, unstable oxides such as silica which act as sources for oxygen, are minimised [390]. A typical chemical composition of a high-alumina brick is 83% alumina and 12% silica with traces of iron oxide.
The isolation of this refining process opened up the possibility that hot iron made via the blast-furnace route can be used to produce bearing steels. Technology was then introduced to expose molten steel to vacuum as a means to reducing the oxygen, hydrogen and nitrogen contents. It is now common for bearing steels to contain less than 10 ppmw of oxygen [118, 391]. It was discovered that the contamination resulting from the transfer of molten steel at the variety of stages can be reduced significantly by the use of shrouds to isolate the streams of liquid steel from the oxygenated environment [392]. The practice of pouring the steel into the top of the ingot mould has largely been replaced by one in which the melt enters the mould from the bottom. This is because top pouring requires a greater number of operations of the slide gate at the bottom of the ladle, allowing reoxidation products to form and fall into the ingot [393]. An additional factor is that during top-pouring, the stream of metal can lack continuity, allowing a greater chance of reoxidation with the oxides ending up in the ingot.
![\includegraphics[width=0.95\textwidth]{steelmaking.eps}](img258.png)
|
There are two main routes to the making of steel for bearings: ingot and continuous casting. The processing paths are illustrated in Fig. 46. There are a lot of subtleties within the broad categories illustrated; procedures are required to maintain cleanliness with respect to inclusions and hydrogen content. For example, argon atmospheres are used to protect the molten steel during teeming, resulting in better homogeneity and cleanliness [1].
![\includegraphics[width=0.8\textwidth]{flow_Baum_1987.eps}](img259.png)
|
In ingot casting, the steel is generally made from about 100 tonnes of scrap charged into an electric-arc furnace, followed by appropriate alloying and vacuum degassing in order to reduce dissolved oxygen, carbon monoxide, hydrogen and nitrogen, and hence the inclusion content [384, 396]. Dissolved carbon becomes a powerful deoxidiser at low pressures, and the product of the deoxidation process, CO, is pumped away so that unlike conventional deoxidising elements such as silicon and aluminium, there are no oxides left behind [397]. The steel is then cast into moulds in such a way that the entrapment of inclusions from the slag in the ladle is avoided. In addition, the moulds are usually bottom fed, to minimise the exposure of the molten metal to air to minimise oxide content.
The iron for continuous casting operations is made either using scarp in an electric arc furnace or from ore in a blast furnace. It is then transferred into a ladle where it is treated with flux and oxygen with the phosphorus concentration reduced to less than 0.01 wt%. The melt is then transferred into a BOFbasic oxygen furnace also called a converter basic oxygen furnace (BOF) to adjust its carbon concentration. At the same time, ferro-chrome is added, which contains unwanted titanium [398] that oxidises and enters the FeO-MnO-Al ![]() O
O ![]() slag in the BOF. However, some of the titanium remains to form carbonitrides which can be quite coarse and hence detrimental to the fatigue properties of the final product. From the BOF, the steel is transferred into another ladle whilst maintaining the slag, for vacuum degassing. It is then continuously cast. Bearing steels made by the continuous casting route combined with all the cleaning technologies are now claimed to outperform those made using the ingot route [395].
slag in the BOF. However, some of the titanium remains to form carbonitrides which can be quite coarse and hence detrimental to the fatigue properties of the final product. From the BOF, the steel is transferred into another ladle whilst maintaining the slag, for vacuum degassing. It is then continuously cast. Bearing steels made by the continuous casting route combined with all the cleaning technologies are now claimed to outperform those made using the ingot route [395].
Segregation is a consequence of the fact that it is impractical to cool the melt at a rate which maintains equilibrium until it becomes fully solidified. Furthermore, the process of freezing does not begin homogeneously in the entire melt, but usually from the mould surface with solidification progressing towards the centre of the casting. The solute enriched liquid is therefore separated from the original solid over a large distance depending on the size of the ingot. There is no practical possibility of eliminating such long-range segregation by diffusion. There are additional phenomena which determine the pattern of macroscopic segregation. The so-called `V'-segregate in continuously cast steel occurs when tensile stresses develop due to differences in thermal gradients across the mushy zone (a mixture of solid and liquid). These cause fracture and the percolation of segregated liquid into the voids thus created [145].
Microsegregation due to cooling at rates inconsistent with homogenisation by diffusion in the solid, is confined to the dimensions of dendrite arm spacings. These spacings have been shown in Fe-Cr-C alloys to be related to solidification conditions and the phase diagram as follows [399]:
![\begin{displaymath} d_p \approx a_8 \frac{[m\overline c_{\rm Cr}(k_{\rm Cr}-1)]^... ...lta T}{m\overline c_{\rm Cr}(k_{\rm Cr}-1)\dot T}\biggr]^{1/3} \end{displaymath}](img260.png) |
(9) |
The composition variations due to microsegregation can be estimated with some accuracy on the basis of simple rules regarding the directional solidification of material with or without diffusion in the solid and mixing in the liquid [400]. In the context of bearing steels such as 52100, the segregation in ingot or continuous casts is determined essentially by the inability of chromium to move sufficiently rapidly within the solid during the course of freezing [401]. Although carbon can migrate at rates many orders of magnitude greater, it tends to associate with the chromium to form carbides.
A chemically segregated alloy in general has disadvantages in the sense that the kinetics of phase transformations and also certain properties will not be homogeneously distributed. This can lead to an uneven distribution of residual stress relative to the axes of symmetry of the component, thus leading to distortion during the subsequent stages of manufacture [242]. The 52100 type steel is sometimes thixoformed at a temperature of about 1390 ![]() C where it is about 45% liquid (Fig. 48) [403, 402] and centreline segregation in particular does not help because it spreads out along the flow lines of the component [404].
C where it is about 45% liquid (Fig. 48) [403, 402] and centreline segregation in particular does not help because it spreads out along the flow lines of the component [404].
In the context of bearing steels, which contain relatively large carbon concentrations, an important consequence of segregation is the deposition of coarse carbides in the carbon and chromium-rich domains. Such aggregates of particles are not conducive to the fatigue resistance of the material. Indeed, excessive segregation of this kind in the 52100 type steels can influence the hot-workability of ingots through the presence of a low melting-temperature eutectic [148, 407, 406, 405], can lead to cracks during deformation at ambient temperatures [408], and reduce the ability to uniformly spheroidise the microstructure thus leading to variable machinability [239]. Coarse carbides can become hard asperities which break through the lubricant film and the resulting contact with the rolling element causes damage in the form of peeling of the raceway surface [409]. Other properties such as tensile strength and work hardening characteristics are not sensitive to the segregation within tolerable limits [410]. It has also been shown that high quality finishing of bearing steel surfaces can be compromised by carbide pull-out during precise grinding operations [411, 412].
One disadvantage of continuous, as opposed to ingot casting, is the tendency to form large carbides along the centre of the casting, although the uniformity in the longitudinal direction can be better than found in ingot casting [48]. The equilibrium phase diagram for steel 52100 (Fig. 4) indicates the solidification austenite exists as a single phase below the solidus temperature, and that the first phase to precipitate in the solid-state is cementite. However, the cooling rate during solidification is in practice greater than consistent with the achievement of equilibrium, and solidification cannot occur homogeneously throughout the melt, but rather begins from the mould surfaces. As a consequence, the liquid in the centre of an ingot is enriched in solute and upon solidification contains significantly larger than equilibrium fractions of coarse carbides.
Such segregation is usually described in terms of a ratio of the carbon concentration in the affected region to the average concentration in the steel. The carbon concentration in a 52100 type steel can typically vary between 0.94-1.07 wt% as a function of position in the casting sequence, and any concentration gradients which translate into the final product can enhance distortion during heat-treatment because of the corresponding variation in transformation characteristics [413]. Much greater maximum values of carbon concentrations, ![]() wt%, and chromium up to to 3.3 wt%, have also been reported [416, 417, 145, 414, 415]; the ratio of the maximum to minimum chromium concentration in the microsegregated regions on a dendritic scale can exceed 4 wt% [400]. Excessive segregation can lead to the formation of a coarse eutectic based on chromium-rich carbides in the equiaxed regions of the ingot, with detrimental effects on the hot-workability of the steel [405]. The eutectic is thought to be ledeburite, in which liquid decomposes to a mixture of austenite and chromium-rich cementite [408, 418], but it has been suggested that the eutectic involves decomposition of liquid into three phases, the austenite, cementite and (Fe,Cr)
wt%, and chromium up to to 3.3 wt%, have also been reported [416, 417, 145, 414, 415]; the ratio of the maximum to minimum chromium concentration in the microsegregated regions on a dendritic scale can exceed 4 wt% [400]. Excessive segregation can lead to the formation of a coarse eutectic based on chromium-rich carbides in the equiaxed regions of the ingot, with detrimental effects on the hot-workability of the steel [405]. The eutectic is thought to be ledeburite, in which liquid decomposes to a mixture of austenite and chromium-rich cementite [408, 418], but it has been suggested that the eutectic involves decomposition of liquid into three phases, the austenite, cementite and (Fe,Cr) ![]() C
C ![]() [406], although the mechanism of such a reaction is not clear. The presence of (Fe,Cr)
[406], although the mechanism of such a reaction is not clear. The presence of (Fe,Cr) ![]() C
C ![]() in the segregated regions has been confirmed using microprobe analysis of the coarse particles in segregated regions of 52100 steel [419]. Some quantitative data for the distribution of inclusions in continuously cast 52100 steel containing an average of 0.012 wt% of sulphur are shown in Table 14. It is known that the segregated bands have a larger than average phosphorus concentration [420] which has a potent effect on cohesion at austenite grain boundaries in strong steels.
in the segregated regions has been confirmed using microprobe analysis of the coarse particles in segregated regions of 52100 steel [419]. Some quantitative data for the distribution of inclusions in continuously cast 52100 steel containing an average of 0.012 wt% of sulphur are shown in Table 14. It is known that the segregated bands have a larger than average phosphorus concentration [420] which has a potent effect on cohesion at austenite grain boundaries in strong steels.
| Columnar | Equiaxed | V-segregate | |
| Percentage area of sulphides | 0.08 | 0.04 | 0.10 |
| Average sulphide size / µm |
6.5 | 41.5 | 68.5 |
| Cr in sulphides / wt% | 10 | 7 | 4 |
| Percentage area of carbides | - 0.05 | 0.44 |
Studies on experimental alloys based on the 52100 composition, but with different carbon concentrations have concluded that a large carbon concentration tends to exaggerate the segregation of chromium into the final liquid to solidify under non-equilibrium conditions. It was speculated that there may be an increase in the partitioning coefficient of chromium between the solid and liquid phases, induced by a ternary interaction with a greater carbon concentration [421]. Figure 47shows that the chromium partitioning into the liquid is not substantially influenced by carbon under equilibriumconditions, but that the carbon segregation is much greater for the carbon-rich alloy.
![\includegraphics[width=0.98\linewidth]{Doherty_1966.eps}](img275.png) |
The segregation and its associated large density of coarse carbides can lead to poor mechanical performance in bearings, and are particularly harmful in conditions where the lubrication fails or in contaminated lubricants [355]; there are many other consequences, for example on the quality of machined surfaces [422]. An additional advantage of making the steel from ore is the reduced concentrations of copper and arsenic relative to steel made using scarp metal. Another variant of the process is rotary continuous casting, where either the water-cooled mould or the bar which emerges from the mould is rotated. It is said that this leads to a reduction in segregation and in the context of bearing steels, results in the same levels of cleanliness and segregation as ingot castings [426, 424, 423, 425]. Normal continuous casting has a segregation pattern similar to that of a small ingot, often described as a `V-segregate' due to its geometry [427], and rotary continuous casting reduces this structure and porosity.
The problem of centre-line segregation in continuous casting can be mitigated by soft reduction, in which the partially solidified strands are mechanically deformed in the presence of liquid at the centre of the strand (Fig. 48). Macroscopic segregation is associated with the flow of interdendritic liquid in the final stages of solidification; the deformation helps to compensate for the solidification shrinkage that drives this liquid flow [430, 432, 428, 429, 431]. It is worth noting that although soft reduction leads to less centreline segregation, greater homogeneity requires prolonged annealing, for example, 16h at 1200 ![]() C [432]. The homogenisation time
C [432]. The homogenisation time ![]() in hours, defined as that which leads to a concentration difference in the matrix of just 1% and absolute temperature
in hours, defined as that which leads to a concentration difference in the matrix of just 1% and absolute temperature ![]() needed are related by the following relation for 52100 type steels [433]:
needed are related by the following relation for 52100 type steels [433]:
Anther method to promote a larger equiaxed solidification structure along the axis of the bloom involves reducing the liquid superheat to less than ![]() C [437]. The excess carbon segregated to the centre in bearing steel blooms is known to increase with the casting superheat and casting speed [417]. Electromagnetic stirring can enhance the equiaxed zone by reducing superheat through convective heat-transfer [438, 437]. However, the method has been found to be only marginally effective in mitigating segregation during the casting of 52100 steels, and even that in circumstances where the casting speed is reduced and when the liquid steel is close to its freezing temperature [416, 417]. Any reduction in casting speed naturally is at the detriment of productivity, and the use of low superheats places significant demands on process control.
C [437]. The excess carbon segregated to the centre in bearing steel blooms is known to increase with the casting superheat and casting speed [417]. Electromagnetic stirring can enhance the equiaxed zone by reducing superheat through convective heat-transfer [438, 437]. However, the method has been found to be only marginally effective in mitigating segregation during the casting of 52100 steels, and even that in circumstances where the casting speed is reduced and when the liquid steel is close to its freezing temperature [416, 417]. Any reduction in casting speed naturally is at the detriment of productivity, and the use of low superheats places significant demands on process control.
|
(a)
![\includegraphics[width=0.50\textwidth]{soft_reduction.eps}](img281.png) (b) (b) ![\includegraphics[width=0.4\textwidth]{Hirt_2005.eps}](img282.png)
|
A recent innovation involves the application of electrical pulses to the semi-solid ingots as a means to stimulate nucleation at the free surface of the melt where the electrical current apparently focusses. The nucleated particles then sink into the underlying liquid, thus changing the coarse solidification microstructure from one dominated by the directional growth of dendrites from the mould surface, into an equiaxed set of grains originating at dendrite fragments dispersed in the liquid [439]. The electropulsing involved peak currents of about 2000 A at a frequency of 200 Hz, for a period of about 60s (the precise details have not been revealed). The columnar to equiaxed transition induced by electropulsing led to a more homogeneous structure and uniform composition in a 52100 steel. It is argued that the heating associated with the current tends to retard the nucleation of dendrites at heterogeneities such as the mould surface, and at the same time reduces their growth rate, thus allowing the particles formed at the surface to make a greater contribution [440]. However, it is not clear why nucleation at the liquid surface is not similarly retarded by the joule heating.
There has been limited work on fabrication of 52100 type bearing steel billets using the spray deposition technique [442, 441]. This method avoids long-range chemical segregation of the type typical with ingot casting since the droplets are partially solidified before they deposit and then rapidly complete solidification, but does not produce a fully dense material even when tubes are spray formed on to austenitic steel bars [443]. The pores are large, typically some 100 µm and with irregular shapes; the microstructural homogeneity can be compromised if there are variations in the cooling rate between the centre and edges of the billet [444]. The distribution of porosity is not uniform (Fig. 49), increasing towards the surface of the billet; the surface is therefore peeled prior to hot-rolling [445]. A comparison of shape changes caused by heat treatment indicates that the more homogeneous spray formed samples exhibit smaller distortion than corresponding samples from continuously cast alloys with greater variations in chemical composition [446]. Anything that favours a uniform phase transformation temperature as a function of position must lead to lower residual stresses, although the scale over which segregation must be reduced is not yet known in order to take advantage of homogeneity.
![\includegraphics[width=0.98\linewidth]{Cui_2004.eps}](img283.png) |
Hot-rolling after deposition does close some of the porosity but there is only cursory evidence that the inclusion content of the deposited material is less than the steel produced by conventional processing, in the form of low-magnification micrographs. A proper inclusion characterisation similar to the methods used for conventional bearing steels is called for. Rolling contact fatigue experiments have yet to be reported. It is surprising that the concentration of impurities such as oxygen have not been reported for the spray-formed billets, given the enormous amount of work in the literature on the critical role of oxides in bearing steels. The spray forming is carried out in an inert environment, but it is not clear how inert this is, and whether the final oxygen concentration depends on the level present in the feed stock. Similar comments apply to 52100 type steel produced using powder metallurgy [447], where the uniformity of the structure is said to be better than in the cast state; it is said that although the oxygen concentration in this case is much higher than in the cast 52100, the oxides are said to be fine and well-dispersed [448]. The 52100 has to be modified with reduced silicon and manganese concentrations down to 1500-2000 ppmw by annealing the powder in hydrogen.
Some very high carbon and solute-rich alloys, such as M62 or CRU80 (Table 8) can only be produced using powder metallurgy in order to obtain any semblance of homogeneity.
A modification of 52100 involving a reduction in the carbon and chromium concentrations and higher manganese content has been investigated with the specific aim of reducing the tendency for centreline carbide stringers in continuously cast blooms and billets from relatively small casters; it has been desginated 80CrMn4 (Table 1). It seems to mimic successfully the important mechanical and thermal processing characteristics of 52100. However, there is no further open literature on this alloy since the original publication [37].
In its ingot-cast form, M1 solidifies in the form of cellular dendrites which are surrounded by large carbides of the MC, M ![]() C and M
C and M ![]() C variety [151]. Although these cellular networks of carbides are broken up by subsequent deformation, they spread out to form the infamous banding. Gas atomisation and consolidation of the resulting powders eliminates this banding. Laser glazing, which involves the melting and rapid re-solidification of the surface to a depth of about 100 µm is effective in eliminating both banding and coarse carbides, whilst at the same time, inducing a compressive stress into the surface. It is noted that M1 is not a usual bearing steel but has historically been considered for aeroengine applications [449].
C variety [151]. Although these cellular networks of carbides are broken up by subsequent deformation, they spread out to form the infamous banding. Gas atomisation and consolidation of the resulting powders eliminates this banding. Laser glazing, which involves the melting and rapid re-solidification of the surface to a depth of about 100 µm is effective in eliminating both banding and coarse carbides, whilst at the same time, inducing a compressive stress into the surface. It is noted that M1 is not a usual bearing steel but has historically been considered for aeroengine applications [449].
The enormous success of vacuum processing has set the standard for clean bearing-steels. In vacuum induction melting (VIM), the cold metal is remelted in a furnace lined with high-purity refractory, and the melt is maintained under a vacuum with encourages the removal of gaseous impurities. A further degree of quality is achieved by vacuum arc remelting (VAR) where the ingot produced in the VIM furnace is made a consumable electrode which is remelted by striking a direct current arc under vacuum. Droplets of liquid drop from the electrode into a water-cooled mould. In the process, some oxides and nitrides dissociate and are pumped away, whereas others become separated by floatation. Vacuum processing does not on the whole change the character of inclusions but does reduce the inclusion content [450].
Vacuum melted steel is in general more susceptible to austenite grain growth than that which has been melted in air [379, 451], largely because the number density of inclusions, and the total surface area of inclusions per unit volume are dramatically reduced [452]. Coarse austenite grains make bearing steels more susceptible to the phenomenon of overheating, in which manganese sulphides liquate at the grain surfaces during heat-treatment [454, 453]. Notwithstanding these difficulties, vacuum melted samples with their lower inclusion content perform better in rolling-contact fatigue tests [451], particularly because of a reduced oxide content [455]. The concentration of oxygen in the steel decreases as the alloy is treated at higher vacuums, Fig. 50[456]. There is some evidence that electroslag refined steels outperform other casting techniques in producing steels which are less susceptible to fatigue failure at the same oxygen concentration, Fig. 97[115]. This is because the distribution of inclusion sizes is shifted towards lower mean values in the electroslag process [457]. Even better results can be obtained by ladle refining using a highly basic slag with a low FeO content, followed by vacuum degassing using the Ruhrstahl-Heraeus process in which steel is circulated between the degassing unit and the transport ladle, and finally the repetition of the ladle refining to remove large inclusions [457]. Advanced processing of this kind has essentially meant that continuous and ingot casting lead to similar qualities of bearing steels [458, 146, 394].
![\includegraphics[width=0.98\linewidth]{vacuum_oxygen.eps}](img284.png) |
Electroslag refining as an additional melt-treatment leads to improvements beyond that achievable from vacuum melting alone; it is known to lead to a reduction in the silicon and more significantly, the phosphorus concentration of the steel [459]. Electroslag remelting sometimes results in better fatigue resistance than vacuum degassed steel, primarily by reducing the incidence of low-life failures [104]. Electroslag refining leaves the steel with a large oxygen concentration, many tens of ppmw [460]. This emphasises a general point [378] that it is not simply a reduction in oxygen content that matters, but a reduction in the size of large inclusions and for a given concentration; a homogeneous distribution of inclusions must also be advantageous. The remelting provides an additional opportunity for large inclusions to be floated off. The process can also be conducted under pressure when nitrogen is an alloying element.
Low levels of critical impurities can apparently be achieved without the vacuum or electroslag remelting, by argon stirring, induction stirring and vacuum degassing of the ladle [461]. Success in this context is classified by the sum of oxygen, titanium and sulphur being less than 80 ppmw. The use of ceramic filters to remove large non-metallic inclusions remains a contender in the search for cleaner steels [378], although the subject does not seem to have made much progress since 1988.
Many bearing steels are ingot cast and the pipe created by the contraction of the liquid on solidification is removed prior to processing. Inadequate cropping of this pipe can lead to the entrapment of very large oxide inclusions, several mm in dimension, in the final processed product [462], Fig. 51. It has been known for a long time that the steel is dirtiest along the axis of the ingot so that rolling contact fatigue improves with distance away from that axis [463].
A further indication of anisotropy in forged samples made from ingots is the fact that fatigue performance is optimum when the angle that the forging direction makes with the rolling contact surface is zero; a large angle in contrast, favours the early onset of damage [465, 64, 463, 464, 3]. Some of this anisotropy, often referred to as `grain flow orientation', is related to the alignment of chemical segregation bands along the primary deformation direction, which may or may not at the same time be associated with excess preponderance of carbides (see for example, Fig. 6 of [465]), and of inclusions depending on the cleanliness of the steel. The bands are known to be favoured crack propagation directions depending on the nature of the stress that the steel is subjected to [467, 466]. Segregated `carbide streaks' and large carbides are known to be damaging in rolling contact fatigue [64]. There is clear evidence that strings of non-metallic particles aligned normal to the contact surface are much more harmful than those parallel to that surface [468]; the Charpy toughness is also sensitive to the orientation relative to the grain flow [469]. Since the occurrence of large carbides is associated with chemical segregation, the problem becomes more severe when the final size of the bar stock is large, since the mechanical reduction from ingot to the bar is then smaller. It is well-established that even in modern clean steels, larger plastic reductions during the manufacture of bar lead to better fatigue properties because the inclusions are broken into finer particles by the deformation [390].
|
(a)
![\includegraphics[width=0.45\textwidth]{Trojahn1.eps}](img285.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Trojahn2.eps}](img286.png)
|
Aluminium has a strong affinity for oxygen and hence is added to bearing-steel melts as a deoxidiser. Most of the added Al combines as Al ![]() O
O ![]() and floats off into the slag assuming that the time available is sufficient for this process. An excessive use of aluminium can reduce the viscosity of the slag, making the electrical arc of the furnace less stable. In practice, particles of alumina greater than about 20 µm tend to be removed into the slag. Any aluminium left in the solidified steel is mostly in the form of alumina particles which can be detrimental to the mechanical properties of the bearing. Typical concentrations of aluminium in the final steel are in the range 0.02-0.04 wt% [456]. For reasons which have not been discussed, ball-bearing steels which are not deoxidised using aluminium have better workability and surface quality following cutting or grinding operations [470].
and floats off into the slag assuming that the time available is sufficient for this process. An excessive use of aluminium can reduce the viscosity of the slag, making the electrical arc of the furnace less stable. In practice, particles of alumina greater than about 20 µm tend to be removed into the slag. Any aluminium left in the solidified steel is mostly in the form of alumina particles which can be detrimental to the mechanical properties of the bearing. Typical concentrations of aluminium in the final steel are in the range 0.02-0.04 wt% [456]. For reasons which have not been discussed, ball-bearing steels which are not deoxidised using aluminium have better workability and surface quality following cutting or grinding operations [470].
Large calcium-containing inclusions are detrimental to the fatigue properties of bearing steels [471]. Calcium-silicon alloys are added to steel for a variety of reasons. Solid alumina inclusions can block casting nozzles, but this problem is reduced by rapid reaction with calcium to form a liquid calcium aluminate [472]. There is, however, a tendency to form a CaO-rich glaze on the ladle used in secondary steelmaking, which can in principle introduce calcium-containing non-metallic inclusions in the melt [389]. The growth rates, at a given oxygen concentration in liquid iron, of calcium and magnesium oxides are significantly smaller than of alumina [473]; this could imply that these oxides are less readily extracted from the steel into the slag by floatation.
Calcium also has a strong affinity for sulphur and hence helps reduce the quantity of sulphides which may influence fatigue behaviour, although some data indicate that the fatigue resistance of 52100 type steel is insensitive to quite large variations in the sulphur concentration [138, 474]. For ![]() -MnS, the expansion coefficient is
-MnS, the expansion coefficient is
![]() over the range 225-591
over the range 225-591 ![]() C and
C and
![]() between 591-928
between 591-928 ![]() C [475]. These values are somewhat smaller than the expansivity of austeniteso that significant stresses may not develop around the sulphide during cooling from elevated temperatures. The expansion coefficient of austenite in 52100 type steel has been measured to be
C [475]. These values are somewhat smaller than the expansivity of austeniteso that significant stresses may not develop around the sulphide during cooling from elevated temperatures. The expansion coefficient of austenite in 52100 type steel has been measured to be ![]() , [476].
, [476].
Inclusions, some of which are listed in Table 15, are problematic in bearing steels for a variety of reasons:
|
(a)
![\includegraphics[width=0.42\textwidth]{Bomas_Alumina.eps}](img290.png) (b) (b) ![\includegraphics[width=0.47\textwidth]{Bomas_empty.eps}](img291.png) (c) ![\includegraphics[width=0.5\textwidth]{Bomas_TiC.eps}](img292.png)
|
Studies have indicated that in modern steels, it is the titanium nitrides and carbonitrides which are most harmful to rolling contact fatigue, followed by oxides (particularly the globular particles which are spinels of calcium and aluminium oxides) and sulphides [128, 471]. Titanium carbonitrides have sharp corners, remain strongly bonded to the matrix and hence crack eventually, leading to a sharp wedge which propagates [484]. This is not the case for alumina particles which debond and hence do not crack. Sulphide coatings on oxides reduce the potency of the oxides to induce damage [485, 128], presumably because the sulphide is able to hot-deform and hence accommodate the incompatibility of plastic strain between the oxide and steel. However, such conclusions cannot be generic and must depend on the method of testing, whether in push-pull or rolling contact loading (section 21.2.3), the detailed chemical composition and processing of the steel concerned. For example, Ti(C,N) of identical size and location as oxides do not seem to induce the formation of butterflies [127].
| Inclusion | Shape | Hardness | Stress | Modulus | ||
| / HV30 | / |
/ GPa | ||||
| 52100 | 750 | 12.5 | 210 | |||
| MnS, CaS | Streaky | 150-170 | 18.1 | Low | 147 | A |
| Al |
Aggregates | 8.0 | Tensile | 387 | B | |
| Ca aluminates | Globular | 900-2500 | 6.5-10.0 | Tensile | 113-350 | B,D |
| CaO.6Al |
8.8 | |||||
| CaO.2Al |
5.0 | |||||
| CaO.Al |
6.5 | |||||
| 12CaO.7Al |
7.6 | |||||
| 3CaO.Al |
10.0 | |||||
| MnO-SiO |
Oblong | 5.0 | Tensile | 73 | C | |
| TiC | Sharp cuboids | 9.4 | Tensile | 320 | T | |
| TiN | Sharp cuboids | 9.4 | Tensile | 320 | T |
There is little doubt that when it comes to hardened, high-carbon steels containing proeutectoid carbides, the fracture toughness is determined by those particles either promoting void formation or initiating cleavage cracks. A large class of such alloys has more or less the same, relatively low level of toughness ( ![]() MPam
MPam ![]() ) once the hardness exceeds about 50 HRC, whereas for lower strength alloys the toughness increases sharply as the hardness (carbon concentration) is reduced [488]. Non-metallic inclusions, dissolved hydrogen and factors such as the austenite grain size can also influence the brittleness of badly processed bearing steels.
) once the hardness exceeds about 50 HRC, whereas for lower strength alloys the toughness increases sharply as the hardness (carbon concentration) is reduced [488]. Non-metallic inclusions, dissolved hydrogen and factors such as the austenite grain size can also influence the brittleness of badly processed bearing steels.
The fracture toughness in mode I loading tends for hardened 52100 type steels have values in the range 15-20 MPam ![]() , the lower values corresponding to larger carbon concentration within the steel [60, 489], Fig. 53. It is possible that some of the observed scatter is due to a factor which has received little attention, anisotropy [490], given that the steels such as M50 and 52100 are deformed into their final shapes and hence will have a distribution in size and shape of inclusions which is not orientation independent.
, the lower values corresponding to larger carbon concentration within the steel [60, 489], Fig. 53. It is possible that some of the observed scatter is due to a factor which has received little attention, anisotropy [490], given that the steels such as M50 and 52100 are deformed into their final shapes and hence will have a distribution in size and shape of inclusions which is not orientation independent.
![\includegraphics[width=0.98\linewidth]{Beswick_toughness.eps}](img302.png) |
Phosphorus is a particular concern in the toughness of strong steels and bearing alloys are no exception [492, 491]. It is an element that is difficult to remove during steelmaking because it is noble with respect to iron during oxygen blowing, so the actual concentration in bearing steels is generally larger than that indicated in Table 3. Phosphorus, along with antimony, tin and arsenic have a potent influence in embrittling the austenite grain boundaries, a phenomenon often expressed empirically using a Bruscato factor ( ![]() ) [493, 494] in order to highlight the relative potency of a variety of tramp elements where
) [493, 494] in order to highlight the relative potency of a variety of tramp elements where
| (11) |
It is interesting that the addition of 0.22 wt% of molybdenum to 52100 steel increases the ultimate tensile strength in the quenched and tempered state from about 2150 to 2450 MPa, even though the proof strength decreases from 1500 to 1400 MPa [29]. Since the steel without molybdenum has negligible ductility, it may be assumed that the higher ultimate strength is because of the greater plasticity of the molybdenum variant, although the original work [29] did not report these details. Any increase in ductility would be consistent with the suppression of embrittlement of the austenite grain surfaces. The original work on the molybdenum modified 52100 was on a steel containing 0.0075 wt% phosphorus and 0.25 wt% molybdenum; they all outperformed Mo-free 52100 in toughness and in rolling contact fatigue performance [28]. Phosphorus may also embrittle by accelerating the formation of cementite at austenite grain surfaces during heat treatment in the ![]() phase field, possibly because it is incorporated in the growing cementite [503].
phase field, possibly because it is incorporated in the growing cementite [503].
The levels of toughness encountered in the best of the hardened 52100 type steels are not enough to cope with severe static or dynamic structural loads, such as those encountered by hub bearings in the automotive industries. As shown in Fig. 12, such a bearing has raceways which are integral with the flanges, and the unit has to be capable of enduring both bearing and structural loads on the wheel of a driven car [88]. To cope with this, the material can be given a special tempering heat treatment which reduces its hardness to about 250HV, which is only slightly higher than the soft-annealed condition at 230HV. However, the ferrite grain size resulting from this so-called `tough temper' is much finer at ![]() µm which compares with tens of micrometers in the soft condition, Fig. 54. This contributes to toughness, whereas the raceways are induction hardened to cope with rolling contact stresses. The hub bearing in effect has a composite microstructure. The toughness values of the soft-annealed and tough-tempered states are 70-80
µm which compares with tens of micrometers in the soft condition, Fig. 54. This contributes to toughness, whereas the raceways are induction hardened to cope with rolling contact stresses. The hub bearing in effect has a composite microstructure. The toughness values of the soft-annealed and tough-tempered states are 70-80 ![]() and 135-145
and 135-145 ![]() respectively [88].
respectively [88].
|
(a)
![\includegraphics[width=0.55\textwidth]{Beswick_1988a.eps}](img307.png) (b) (b) ![\includegraphics[width=0.33\textwidth]{Beswick_1988b.eps}](img308.png)
|
Some surprisingly large values of the fracture toughness, in the range 42-52 ![]() have been reported for 52100 type steel in the quenched and tempered martensitic condition, and when isothermally transformed into mixed microstructures of bainite and martensite [176]. The hardness of all the samples tested exceeded 59 HRC. However, the toughness tests were carried out using non-standard procedures, i.e.,with the fatigue-induced pre-crack replaced by a spark-machined slit so these are not valid data. It has been argued that three-point chevron-notched specimens can be used to determine the fracture toughness without pre-cracking the samples [504]. Samples with these notches were tested with and without pre-cracking and yielded quite high fracture toughness values from 41-53
have been reported for 52100 type steel in the quenched and tempered martensitic condition, and when isothermally transformed into mixed microstructures of bainite and martensite [176]. The hardness of all the samples tested exceeded 59 HRC. However, the toughness tests were carried out using non-standard procedures, i.e.,with the fatigue-induced pre-crack replaced by a spark-machined slit so these are not valid data. It has been argued that three-point chevron-notched specimens can be used to determine the fracture toughness without pre-cracking the samples [504]. Samples with these notches were tested with and without pre-cracking and yielded quite high fracture toughness values from 41-53 ![]() for samples of 52100 steel heat treated to give hardnesses in the range 60-63 HRC. The significance of these high values of toughness is not clear in terms of comparisons against standard tests.
for samples of 52100 steel heat treated to give hardnesses in the range 60-63 HRC. The significance of these high values of toughness is not clear in terms of comparisons against standard tests.
The speed at which a crack propagates is determined by a parameter known as the dynamic stress intensity ![]() ; it represents the material's resistance to dynamic crack growth and is often referred to as a dynamic fracture toughness, although it is not a single valued material parameter as
; it represents the material's resistance to dynamic crack growth and is often referred to as a dynamic fracture toughness, although it is not a single valued material parameter as ![]() .
.
The speed of the crack increases rapidly with the magnitude of the dynamic stress intensity but eventually reaches some terminal velocity beyond which it becomes insensitive to ![]() . The value of
. The value of ![]() at which the crack speed becomes zero ( i.e.the crack arrests) is designated
at which the crack speed becomes zero ( i.e.the crack arrests) is designated ![]() and is usually smaller than
and is usually smaller than ![]() since the stress intensity required to initiate a crack is usually greater than that to propagate it. Fig. 55illustrates the dynamic stress intensity measured at a crack speed of 2ms
since the stress intensity required to initiate a crack is usually greater than that to propagate it. Fig. 55illustrates the dynamic stress intensity measured at a crack speed of 2ms ![]() for 52100 steel samples taken from tubes, quenched after austenitisation at a variety of temperatures followed by tempering at 160
for 52100 steel samples taken from tubes, quenched after austenitisation at a variety of temperatures followed by tempering at 160 ![]() C for 1.5h [505]. It is not clear why the cold-rolled tubes perform better than those which were heat treated from the hot-rolled condition. Blunt-notch impact tests reveal a similar correlation, that cold-working of the steel prior to the heat-treatment needed to produce martensite leads to an improvement in the energy absorbed, although
C for 1.5h [505]. It is not clear why the cold-rolled tubes perform better than those which were heat treated from the hot-rolled condition. Blunt-notch impact tests reveal a similar correlation, that cold-working of the steel prior to the heat-treatment needed to produce martensite leads to an improvement in the energy absorbed, although ![]() was not similarly enhanced [60]. The mechanism is unrelated to refinement since other methods of achieving smaller austenite grains did not lead to better toughness. There are data showing that cold deformation leads to an increase in the density of the steel [505] but the mechanism for this is not clear since the original interpretation that the introduction of defects into the microstructure causes densification is incorrect [506, 507].
was not similarly enhanced [60]. The mechanism is unrelated to refinement since other methods of achieving smaller austenite grains did not lead to better toughness. There are data showing that cold deformation leads to an increase in the density of the steel [505] but the mechanism for this is not clear since the original interpretation that the introduction of defects into the microstructure causes densification is incorrect [506, 507].
![\includegraphics[width=0.98\linewidth]{Dynamic_Beswick_1993.eps}](img311.png) |
The Charpy impact properties of bearings steels are expected to be poor when compared with values typical of the much lower strength structural steels. Undissolved cementite or other coarse carbide particles do not help in this respect. Impact energy measured on un-notched 10mm diameter cylinders give values in the range 48-71J, measured at room temperature, have been reported for 52100 type steel [176]. Another study where the sample shape was not specified reports an impact energy range of 43-74J [508].
Given that the notch toughness of traditional bearing steels in their hardened condition is limited, it is found that the presence of a notch dominates crack initiation during rotating-bending fatigue tests, rather than inclusions. Thus, inclusions are not found on the fracture surfaces of tests on notched samples, whereas the origin of the fatigue crack can be traced to an inclusion when un-notched samples are used [509].
Fatigue is intriguing because in well-designed structures it occurs slowly and leads eventually to failure at stresses much smaller than those associated with the breaking strength of the material. To paraphrase Wöhler [510], rupture may be caused by the repeated application of stresses, none of which equal the carrying strength [511].
There are two kinds of fatigue tests where explicit stress concentrations are avoided so that phenomena related to crack initiation can be investigated. In one case, a smooth sample is rotated whilst it is bent so that the surface undergoes cyclic tension and compression with each revolution. The distribution of stress through such a sample is not uniform and there is a neutral axis where the stress is zero. In the another test, a sample is loaded axially so that the gauge length is uniformly stressed, with the advantage that a larger volume of material is exposed to the stress, making the detection of inclusion initiated fatigue more likely. This difference between the bending and axial modes on the exposed volume seems well-established and yet there are still experiments being reported to reach the same conclusion [512]. The results in both cases are expressed as `` ![]() -
- ![]() " curves, by plotting the alternating stress amplitude
" curves, by plotting the alternating stress amplitude ![]()
![]() Stress amplitude in fatigue versus the logarithm of the number of cycles
Stress amplitude in fatigue versus the logarithm of the number of cycles ![]() that cause failure,
that cause failure, ![]() Number of fatigue cycles for failure Fig. 56.
Number of fatigue cycles for failure Fig. 56.
![\includegraphics[width=0.98\linewidth]{SN.eps}](img313.png) |
Materials which strain-age exhibit a fatigue limit ![]() , which is the value of
, which is the value of ![]() below which failure in principle does not ever occur during cyclic loading. The limit is usually ascribed to dynamic strain-ageing in which the mobile dislocations are pinned by interstitials. Another view is that the limit should be identified with the need for plasticity to spread across grain boundaries for the successful propagation of cracks [514, 515, 513].
below which failure in principle does not ever occur during cyclic loading. The limit is usually ascribed to dynamic strain-ageing in which the mobile dislocations are pinned by interstitials. Another view is that the limit should be identified with the need for plasticity to spread across grain boundaries for the successful propagation of cracks [514, 515, 513].
For materials which do not exhibit a fatigue limit, it is conventional to define an endurance limit 14 Bearing steels might fall into this category [26] and data from fatigue tests carried out to a billion cycles seem to confirm this [516, 517].
Recent work based on torsion testing has confirmed that there is no observable fatigue limit for the 52100 type steel heat-treated to a hardness range 58-62 HRC [518]. The existence of a true fatigue limit for bearing alloys was in doubt as long ago as 1936 ([519], cited in [518]). Assuming that strain-ageing, in which carbon atoms render dislocations sessile, is responsible for creating a fatigue limit, the absence of the limit could be explained by the existence of mobile dislocations in the martensitic or bainitic steels, or because the microstructure is intrinsically heterogeneous and hence leads to stress concentrations which stimulate dislocation mobility. Indeed, it is possible by inducing strain ageing to increase the endurance limit for 52100 steel in its spheroidised [520] and hardened [521] states. The issue of whether or not a true fatigue limit exists is important in the application of empirical equations of the type used in defining bearing life, as discussed in section 17.2.
The endurance limit ![]() , which is identified as the stress amplitude corresponding to a fatigue life of say
, which is identified as the stress amplitude corresponding to a fatigue life of say ![]() , has to be chosen so as to reflect the life of the component. For example, the endurance limit was historically set at
, has to be chosen so as to reflect the life of the component. For example, the endurance limit was historically set at ![]() but many modern bearings are designed to last much longer and hence utilise a larger limit of
but many modern bearings are designed to last much longer and hence utilise a larger limit of ![]() Cycles. The definition of the endurance limit is clear in tests where samples are uniaxially loaded (axial or rotating bending), but it is also used in the context of more the complex stress systems associated with rolling contact, to describe the contact pressure which avoids failure for
Cycles. The definition of the endurance limit is clear in tests where samples are uniaxially loaded (axial or rotating bending), but it is also used in the context of more the complex stress systems associated with rolling contact, to describe the contact pressure which avoids failure for ![]() [118]. In summary [522],
[118]. In summary [522],
| (12) |
Cracks initiate at the free surface of a homogeneous sample either due to the existence of stress concentrations, for example from machining marks, the intersection of grain boundaries with the surface, due to the development of slip steps at the free surface, from surface-breaking inclusions [524] or even unfavourable crystallographic orientations [525]. Fatigue experiments are done under conditions where the maximum stress is less than the macroscopically measured yield strength ![]() . As a result, the mechanisms for the surface initiation of fatigue cracks usually predominate at relatively large applied stresses, as will become apparent in the discussion of fatigue data that follows.
. As a result, the mechanisms for the surface initiation of fatigue cracks usually predominate at relatively large applied stresses, as will become apparent in the discussion of fatigue data that follows.
It is intriguing why surface initiation becomes more difficult at low stress amplitudes, so that cracks begin instead from sub-surface non-metallic inclusions [125] or embrittled prior-austenite grain boundaries [527, 526], Fig. 57. This change in the location of fatigue failure is a general observation not restricted to bearing steels [528]. Surfaces of fatigue tensile-test samples are often prepared by gentle grinding or fine machining to ensure a roughness which does not exceed a few micrometers. This process introduces longitudinal stresses up to about ![]() MPa, which even after electropolishing to a depth of 20 µm, remain to a level of about
MPa, which even after electropolishing to a depth of 20 µm, remain to a level of about ![]() MPa [181, 529]. These compressive stresses counteract the applied force in tension so that surface initiation should predominate only at large stresses. Compressive surface stresses introduced by shot-peening lead to a transfer of the fatigue initiation site from the surface to sub-surface even at high cyclic stress [530]; as expected, the fatigue life of sub-surface initiated fracture does not change when this happens. Similarly, the removal of surface stresses by electropolishing transfers the initiation site to the surface even at low stress amplitudes [529]. Specimens which are circumferentially notched, and hence contain stress gradients which focus at the surface, inevitably fail by fatigue crack initiation at the surface [482, 529].
MPa [181, 529]. These compressive stresses counteract the applied force in tension so that surface initiation should predominate only at large stresses. Compressive surface stresses introduced by shot-peening lead to a transfer of the fatigue initiation site from the surface to sub-surface even at high cyclic stress [530]; as expected, the fatigue life of sub-surface initiated fracture does not change when this happens. Similarly, the removal of surface stresses by electropolishing transfers the initiation site to the surface even at low stress amplitudes [529]. Specimens which are circumferentially notched, and hence contain stress gradients which focus at the surface, inevitably fail by fatigue crack initiation at the surface [482, 529].
|
(a)
![\includegraphics[width=0.45\textwidth]{Sakai_axial.eps}](img325.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Sakai_bending.eps}](img326.png)
|
Attempts have been made to interpret the data such as those presented in Fig. 57in terms of two ![]() -
- ![]() Curves, representing surface and interior crack nucleation sites [516, 25]. The utility of such a representation is not clear, and indeed is not distinct in many experimental data [531]. And of course, it is necessary to consider the relevance of such tests in the context of the particular application.
Curves, representing surface and interior crack nucleation sites [516, 25]. The utility of such a representation is not clear, and indeed is not distinct in many experimental data [531]. And of course, it is necessary to consider the relevance of such tests in the context of the particular application.
Perhaps the focus needs to be on why the failure initiation shifts to the surface at large stresses; it seems likely that the observations are due to an inadequate accounting for compressive stresses existing in the test-sample surface, left over for example, from machining operations. This conclusion is backed by work which shows with clarity that the transition from sub-surface to surface initiation can be induced by gentle grinding of the sample surface in order to introduce shallow ( ![]() m) compressive stresses into the surface [532, 533]. Indeed, if circumstances are such that the compressive stress is relaxed gradually during testing, then the focus of fracture once again shifts to the surface. Surface decarburisation can dramatically influence both the magnitudes of the stresses in an
m) compressive stresses into the surface [532, 533]. Indeed, if circumstances are such that the compressive stress is relaxed gradually during testing, then the focus of fracture once again shifts to the surface. Surface decarburisation can dramatically influence both the magnitudes of the stresses in an ![]() -
- ![]() Curve, and the transition from surface to interior initiation as the stress is reduced [24]. In some cases the so-called duplex
Curve, and the transition from surface to interior initiation as the stress is reduced [24]. In some cases the so-called duplex ![]() -
- ![]() Curve appears in rotating bend tests but not in axially loaded samples, emphasising again the role of the surface [534].
Curve appears in rotating bend tests but not in axially loaded samples, emphasising again the role of the surface [534].
Fractographic studies of failed ![]() -
- ![]() samples reveal failure modes in three categories. When cracks initiate at the surface, there is a half-penny shaped smooth fatigue-crack (Fig. 58a, [i]) front that propagates into the sample, followed by a rougher region (Fig. 58a, [ii]) where grains have detached at their austenite boundaries, and then rapid fracture containing river lines consistent with the direction in which a fast fracture proceeds. It is suggested [125, 535] that region [i] is generated by the steady advance of a fatigue crack as the stress intensity range exceeds the threshold value
samples reveal failure modes in three categories. When cracks initiate at the surface, there is a half-penny shaped smooth fatigue-crack (Fig. 58a, [i]) front that propagates into the sample, followed by a rougher region (Fig. 58a, [ii]) where grains have detached at their austenite boundaries, and then rapid fracture containing river lines consistent with the direction in which a fast fracture proceeds. It is suggested [125, 535] that region [i] is generated by the steady advance of a fatigue crack as the stress intensity range exceeds the threshold value ![]() . The front dividing regions [i] and [ii] is defined by the locus of all points where
. The front dividing regions [i] and [ii] is defined by the locus of all points where ![]() .
. ![]() Threshold stress intensity range for crack propagation in tensile mode I As the stress intensity increases due to crack growth, region [ii] develops with a rough fracture surface corresponding to crack propagation by grain boundary failure. Final failure occurs when the stress intensity at the crack tip reaches the critical value
Threshold stress intensity range for crack propagation in tensile mode I As the stress intensity increases due to crack growth, region [ii] develops with a rough fracture surface corresponding to crack propagation by grain boundary failure. Final failure occurs when the stress intensity at the crack tip reaches the critical value ![]() , the fracture toughness of the material.
, the fracture toughness of the material. ![]() Mode I fracture toughness For 52100 type steel,
Mode I fracture toughness For 52100 type steel,
![]() and
and ![]() [125].
[125].
Fig. 58b shows a classic `fish-eye' fracture surface due to crack initiation at an inclusion. The features are essentially the same as a surface-initiated crack except that the shape of the fatigue crack is that of a complete penny rather than a half-penny; fish-eyes can be elliptical in shape when they develop in heterogeneous stress fields, for example when the surface layers are hardened and placed in compression, or when bending moments are applied during fatigue [536]. For the same reason, the size of fish-eyes may not be uniform; the dimensions increase as a function of depth below the compressed surface of nitrided or carburised components [536]. In Fig. 58c the crack has initiated at an inclusion but in the proximity of the surface, so that a part of it has reached the surface, giving rise to a so-called `contact fish-eye'.
It has been suggested that cryogenic treatment of 52100 steel can lead to improvements in the endurance limit as measured during rotating-bending tests, possibly due to the precipitation of fine carbides [180]. However, there is no proof or mechanism proposed to show why carbides should precipitate at -196 ![]() C, and the observed changes in endurance limit are rather small and may not be significant when scatter. Another study investigated differences between cryogenic treatment at 77K and 193K, but no attempt was made to measure the retained austenite content and the level of characterisation was in general too coarse to draw significant conclusions [537]. The subject of cryogenic treatment and its effects has been thoroughly reviewed in the context of tool steels [538] and it is possible that the influence of cold treatments is not simply on the retained austenite content, but studies are called for where the mechanisms of any effects are established with some clarity.
C, and the observed changes in endurance limit are rather small and may not be significant when scatter. Another study investigated differences between cryogenic treatment at 77K and 193K, but no attempt was made to measure the retained austenite content and the level of characterisation was in general too coarse to draw significant conclusions [537]. The subject of cryogenic treatment and its effects has been thoroughly reviewed in the context of tool steels [538] and it is possible that the influence of cold treatments is not simply on the retained austenite content, but studies are called for where the mechanisms of any effects are established with some clarity.
|
(a)
![\includegraphics[width=0.75\textwidth]{surface_Peet.eps}](img332.png) (b) ![\includegraphics[width=0.45\textwidth]{Sakai_fish.eps}](img333.png) (c) (c) ![\includegraphics[width=0.45\textwidth]{Sakai_contact.eps}](img334.png)
|
Rotating-bending fatigue machines can achieve loading frequencies of about 50Hz and servohydraulic testers some 400-1000Hz [540]. In contrast, piezoelectric devices are used to test smooth samples using axial loading or torsion, at frequencies in the range 20-100kHz in order to reasonably rapidly achieve fatigue data up to ![]() Cycles [543, 541, 542].
Cycles [543, 541, 542].
Testing in tension-compression involves keeping a constant displacement amplitude during the test. For most of the fatigue life there is little difference in specimen loading between stress and strain controlled experiments until the fatigue crack becomes large. [544]. The specimen in ultrasonic fatigue vibrates in resonance with the stimulus and the sample is designed so that the point half way along its length is a displacement node where the stress is maximum [546, 545]. Hour-glass shaped samples are normally used. Parallel gauge lengths may be introduced in order to increase the volume at risk, although the distribution of stress within that length will not be uniform. On the other hand, samples can be designed so that the variation of stress within the straight section is small [547].
Conventional tests for some 10 ![]() Cycles would take more than a decade to complete, whereas with a 100kHz ultrasonic machine, the test would be completed in less than 300h. The samples can be notched in order to introduce stress concentrations. There are important factors to bear in mind with high frequency tests:
Cycles would take more than a decade to complete, whereas with a 100kHz ultrasonic machine, the test would be completed in less than 300h. The samples can be notched in order to introduce stress concentrations. There are important factors to bear in mind with high frequency tests:
Fig. 59compares data obtained in a conventional test at 50Hz [125] and those measured using 20kHz ultrasonic loading [543]. The two sets deviate substantially at all stages of life where a comparison can be made. For ![]() , both kinds of tests are dominated by failure at inclusions within the steel rather than by crack propagation from the surface.
, both kinds of tests are dominated by failure at inclusions within the steel rather than by crack propagation from the surface.
![\includegraphics[width=0.98\linewidth]{gigacycle.eps}](img338.png) |
It is not entirely clear why there is a discrepancy between the two kinds of tests, with the ultrasonic tests consistently indicating lower fatigue strength. This is in contrast, for example, to the behaviour of aluminium alloys where high-frequency testing yields a significantly greater fatigue life at all stress amplitudes [540]. The minimum diameters of the samples studied are identical for the two kinds of tests, at 3mm; the volume of material exposed to the maximum stress should therefore be similar. The samples used to generate all the results illustrated in Fig. 59are ``hour-glass" in shape, i.e.,they have no parallel gauge length. Furuya [547] has shown that the volume of material at risk can be altered by controlling the extent of the parallel gauge length, in which case the fatigue properties deteriorate as the volume of highly-stressed material is increased. The probability of finding critical inclusions in the test sample increases when the volume is large, except when damage initiates from the specimen surface. These considerations do not of course explain the discrepancy illustrated in Fig. 59.
Fig. 60shows a more comprehensive comparison between conventional and ultrasonic data. The underestimation of fatigue strength by high-frequency testing is maintained for all frequencies where comparisons can be made. The reproducibility of the martensitic steel data for SUJ2 is impressive given the independent sources of the data, but a significantly different behaviour is observed when martensitic 100Cr6 is tested. The bainitic and martensitic structures from the same steel show a similar fatigue strength in the gigacycle regime. Detailed analysis is not possible since the specimen geometry and specific heat treatments were not quoted in [554].
Also plotted in Fig. 60are 30 Hz tests [555] which have a much lower fatigue strength than the data reported in [125]. The reason for this discrepancy is not clear and specimen dimensions are not stated in the original publication [555], but it led Baudry et al.to conclude that gigacycle tests are validated as a reliable tool for fatigue assessment.
![\includegraphics[width=0.98\linewidth]{Almaraz2.eps}](img339.png) |
Furuya [547] concludes that large specimens should be used when conducting gigacycle fatigue tests. However, this applies also to conventional low-frequency tests. The important point is to use a sample size consistent with the goal of the experiment, and to use the same risk volume for both conventional and ultrasonic tests if comparisons are to be made.
It may be speculated that the larger strain rates associated with 20kHz testing makes the steel behave in a more brittle manner - an increase in strain rate is known to raise the shear yield strength in bearing steels [17]. This hypothesis is consistent with data on lower strength steel, illustrated in Fig. 61, where the difference between the ultrasonic and conventional testing is small. The formation of slip bands during testing usually degrades fatigue life because the deformation is heterogeneous and hence intense. It has been demonstrated that in a ductile steel containing only 0.13 wt% carbon, slip bands form during conventional testing but not at ultrasonic loading frequencies, leading to a greater fatigue life [553]. This phenomenon presumably is not relevant in bearing steels which are brittle and hard.
![\includegraphics[width=0.98\linewidth]{Furuya_2010.eps}](img340.png) |
Figure 62illustrates ultrasonic fatigue data from samples which were electropolished in order to reduce the compressive surface residual-stresses that arise when the tensile samples are ground. The results for the steel in the bainitic condition are particularly interesting because there isn't much of a difference between surface and interior initiated failure, emphasising the role of the ratio of residual to applied stress in determining whether damage begins at the free surface or at inclusions within the steel. The figure includes for comparison purposes, data from the alloy in its quenched and tempered condition; these tests were on an hour-glass shaped sample exposed to a relatively smaller risk volume. In spite of this, the bainitic microstructure shows better fatigue resistance presumably because of its greater ductility.
Mayer et al.[557] have conducted variable amplitude fatigue tests; the accumulated damage ![]() at any point in the test is approximated by
at any point in the test is approximated by
![\includegraphics[width=0.98\linewidth]{Mayer.eps}](img346.png) |
The discussion of push-pull and rotating bending tests highlights the sensitivity of the method to specimen design and risk volume, and of the state of the surface both in terms of roughness and with regard to stresses residing in the specimen surface as vestiges of sample preparation. Tests involving bending expose a smaller volume to damaging stresses when compared with push-pull tests; they therefore are associated with greater fatigue lives, Fig. 63. For the same reason, hour-glass shaped samples will give better performance push-pull tests than those with long, parallel gauge lengths. And larger diameter samples should fail after fewer cycles because the probability of finding large inclusions increases with the exposed volume.
The data from these experiments cannot be used to assess the performance of the material in rolling contact fatigue. Neither the stresses, the shape of the imposed stress cycle, nor the failure mechanisms are identical for uniaxial and rolling contact tests. The question then arises as to why this method remains popular as a method of studying the fatigue properties of bearing steels:
![\includegraphics[width=0.98\linewidth]{Nakajima_2010.eps}](img348.png) |
It is not entirely clear why uniaxial fatigue tests on bearing are conducted using an ![]() ratio of
ratio of ![]() . This does not approximate what happens in rolling contact fatigue where mode II sliding shear is relevant, and is better represented as a combination of torsion and compression. It is known that tests conducted using
. This does not approximate what happens in rolling contact fatigue where mode II sliding shear is relevant, and is better represented as a combination of torsion and compression. It is known that tests conducted using ![]() given better fatigue lives than
given better fatigue lives than ![]() [175], presumably because it is the shear stresses which matter in the initiation of cracks at inclusions, and also because the stress range is greater in the latter case.
[175], presumably because it is the shear stresses which matter in the initiation of cracks at inclusions, and also because the stress range is greater in the latter case.
![]() Fatigue crack length or half-length for surface breaking cracks
Fatigue crack length or half-length for surface breaking cracks ![]() Exponent in Paris law for fatigue crack growth per cycle
Exponent in Paris law for fatigue crack growth per cycle ![]() Critical value of stress intensity which leads to unstable crack propagation
Critical value of stress intensity which leads to unstable crack propagation
There are circumstances in which the life of a component is limited by the rate at which cracks grow rather than by the crack initiation event. The fracture mechanics approach addresses the advance of sharp cracks per cycle of fatigue loading ( ![]() ) as a function of the stress intensity range
) as a function of the stress intensity range ![]() . Figure 64illustrates the general trend with perceptible growth beginning at a threshold value
. Figure 64illustrates the general trend with perceptible growth beginning at a threshold value ![]() , followed by a Paris law regime in which
, followed by a Paris law regime in which
![\includegraphics[width=0.98\linewidth]{Paris.eps}](img357.png) |
Typical values of the crack advance per cycle for 52100 steel are illustrated in Fig. 65, where it is seen that an increase in the austenitisation temperature leads to more rapid crack growth whereas higher tempering temperatures are associated with lower crack rates [60]. Both of these effects are related to the amount of carbon in solid solution within the martensite, since a higher concentration makes the martensite more brittle. The threshold ![]() in mode I loading is in the range 3.3-8.3
in mode I loading is in the range 3.3-8.3 ![]() [60]. The threshold value can be sensitive to microstructure but effect is not large for strong steels [560], and bearing steels fall into this category. Other modes of loading, involving shear, are particularly important in the context of rolling contact fatigue are discussed at length in section 15.3.
[60]. The threshold value can be sensitive to microstructure but effect is not large for strong steels [560], and bearing steels fall into this category. Other modes of loading, involving shear, are particularly important in the context of rolling contact fatigue are discussed at length in section 15.3.
![\includegraphics[width=0.98\linewidth]{Beswick_fatigue.eps}](img358.png) |
As might be expected, fatigue crack growth rates decrease when the crack front encounters a compressive stress in case-hardened steels, and if the carburising results in a tensile residual stress field, then the crack accelerates [562, 343, 561]. The influence of residual stress during fatigue crack growth can be approximated by combining the applied stress intensity with another term (an effective stress intensity, [343]) given by ![]() where
where ![]() is the internal stress with the appropriate sign, and
is the internal stress with the appropriate sign, and ![]() is an empirical distance loosely associated with the depth over which the internal stress pattern exists.
is an empirical distance loosely associated with the depth over which the internal stress pattern exists.
Fig. 66compares the crack growth rates observed in 52100 steel and M50 steels, both in their through hardened conditions. The M50 steel exhibits a significantly slower growth rate, presumably because of the vacuum induction melting and vacuum arc remelting procedures implemented in its manufacture, and possibly the absence of cementite particles that exist in the 52100 alloy.
![\includegraphics[width=0.98\linewidth]{crack_growth.eps}](img363.png) |
The fatigue life of bearings is determined primarily by three factors [563]: the detachment of material (spalling) following the initiation of cracks below the contact surface, spalling due to surface irregularities and due to distresscaused by surface roughness or inadequate lubrication. Surface roughness is also related quantitatively to vibration levels [564]. We shall primarily be concerned in this review with the first two of these failure mechanisms and mostly with sub-surface initiated fracture. Modern bearing steels are clean but inclusions persist, and surface initiated fracture usually is associated with loads which are well above the design specifications.
The analysis presented here is for an idealised situation involving only elastic deformation, and as such is not fully representative of what happens in rolling contact during the operation of bearings. This is because the surface of a rolling element or raceway will tend to be rough and the pressures may be sufficiently large to cause a certain amount of plasticity. The formalism is nevertheless useful in illustrating the consequences of rolling contact, and as will be seen later, may become representative once the material has work hardened during the course of operation. However, for detailed quantitative work which also attempts to estimate the development of residual stress, a full three-dimensional elastic-plastic model which includes work-hardening must be used [565].
The stress field created when two frictionless bodies are pressed together into elliptical contact whilst avoiding plasticity was first studied by Hertz [567, 566]. If the curvatures of the two stationary solids of revolution are ![]() and
and ![]() respectively, then
respectively, then ![]() Relative curvature
Relative curvature ![]() is the relative curvature given by
is the relative curvature given by ![]() . A full discussion for a variety of contact geometries is available in [567], but assuming a circular contact area of radius
. A full discussion for a variety of contact geometries is available in [567], but assuming a circular contact area of radius ![]() Radius of contact area
Radius of contact area ![]() , the variation of pressure
, the variation of pressure ![]() Contact pressure
Contact pressure ![]() as a function of distance
as a function of distance ![]() from the centre of the contact area, given by [567, 566]
from the centre of the contact area, given by [567, 566]
The corresponding ![]() Radial stress radial and
Radial stress radial and ![]() Tangential stress tangential stresses within the contact circle, at the surface are given by:
Tangential stress tangential stresses within the contact circle, at the surface are given by:
![$\displaystyle \frac{1-2\nu}{3} \frac{r_0^2}{r^2}\biggl(1-\biggl[1-\frac{r^2}{r_0^2}\biggr]^{3/2}\biggr) - \sqrt{1-\frac{r^2}{r_0^2}}$](img380.png) |
|||
![$\displaystyle -\frac{1-2\nu}{3} \frac{r_0^2}{r^2}\biggl(1-\biggl[1-\frac{r^2}{r_0^2}\biggr]^{3/2}\biggr) - 2\nu\sqrt{1-\frac{r^2}{r_0^2}}$](img382.png) |
(16) |
| (17) |
|
(a)
![\includegraphics[width=0.45\textwidth]{hertz_coordinates.eps}](img384.png) (b) ![\includegraphics[width=0.45\textwidth]{hertz_pressure.eps}](img385.png) (c) (c) ![\includegraphics[width=0.45\textwidth]{Hertz_radial.eps}](img386.png)
|
![\begin{displaymath} \frac{\sigma_r}{p_0}=\frac{\sigma_\theta}{p_0} = -(1-\nu)\bi... ...r\} \biggr]+\frac{1}{2}\biggl(1+\frac{z^2}{r_0^2}\biggr)^{-1} \end{displaymath}](img388.png) |
(18) |
 |
(19) |
| (20) |
The equivalent stress, often known as the von Mises stress, is given by
| (21) |
![\includegraphics[width=0.98\linewidth]{contact_shears.eps}](img398.png) |
Many studies have been conducted to study which shear stress, ![]() ,
, ![]() or the von Mises shear stress is most damaging in the context of fatigue [302, 314]. Their roles can in principle be determined by comparing the respective stress distributions against the location of maximum damage in experiments; thus, cracks have been observed to initiate at inclusions located at the shallower depth corresponding to the orthogonal shears [147]. However, whichever shear stress is considered, the maximum occurs below the contact surface and as will be seen later, this has significant consequences to the development of damage. Notice that the shear stress is proportional to the contact pressure
or the von Mises shear stress is most damaging in the context of fatigue [302, 314]. Their roles can in principle be determined by comparing the respective stress distributions against the location of maximum damage in experiments; thus, cracks have been observed to initiate at inclusions located at the shallower depth corresponding to the orthogonal shears [147]. However, whichever shear stress is considered, the maximum occurs below the contact surface and as will be seen later, this has significant consequences to the development of damage. Notice that the shear stress is proportional to the contact pressure ![]() but the proportionality constant will depend on the ellipticity of the contact. The ellipticity defined as the ratio of the minimum to maximum diameters is typically 0.80 for the inner race of a bearing [570].
but the proportionality constant will depend on the ellipticity of the contact. The ellipticity defined as the ratio of the minimum to maximum diameters is typically 0.80 for the inner race of a bearing [570].
If plastic yielding is avoided, then the contact will not leave any residual stresses or damage after the loading cycle is completed. If the yield criterion is however, exceeded, then there are three phenomena which occur during cyclic contact [571] 15 :
| Shakedown pressure / MPa | Operating pressure / MPa | ||
| Steel 52100 | Steel 1070 | ||
| Line contact ( |
2040 | 2560 | 1400-1800 |
| Point contact ( |
2400 | 3010 | 2000-2800 |
The shakedown limit will be different in a material which in its initial unloaded state contains residual stresses. Furthermore, a steel containing retained austenite will have a longer shakedown period than one which does not, because the progressive transformation of the austenite into martensite under the influence of stress [565]. On the other hand, the work-hardening resulting from the formation of fresh martensite leads to a smaller plastic strain prior to the achievement of the shakedown condition; this is reflected in the development of a smaller groove depth during rolling contact [565]. According to Voskamp [575] the first stage of bearing operation leads to the transformation of austenite and cyclic hardening, with prolonged rolling contact causing microstructural changes that are associated with cyclic softening so that the shakedown limit is exceeded and damage accumulation accelerates, leading finally to failure. The details of these microstructural changes are discussed in section 21.
The shakedown process can be visualised more simply in terms of a constant applied-stress fatigue test. The alternating stress amplitude is therefore fixed but the plastic strain per cycle decreases as the material cyclically hardens, until eventually the strain ceases to increase on a macroscopic scale [bainite" id="tex2html676">100, 576], Fig. 70a. The reduction progressive in plastic strain during cyclic loading is illustrated in Fig. 70b for 52100 steel in its martensitic and bainitic conditions. In the former case, it is the decomposition of retained austenite during the early stages that contributes to the plastic strain recorded, whereas the absence of retained austenite in the bainitic condition means that the total plastic strain is rather small at all stages of deformation. Cyclic deformation is discussed in more detail in section 5.3.
|
(a)
![\includegraphics[width=0.45\textwidth]{Kettunen.eps}](img402.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Christ_cyclic.eps}](img403.png)
|
Whereas the discussion here has focused on deformations that occur as a consequence of contact, the implementation of the bearing into service can introduce additional stresses which have a dramatic influence on the fatigue behaviour. Bearings are sometimes press-fitted on to shafts, a process which introduces hoop stresses, and the speed of rotation speed can give rise to significant centrifugal forces which are greatest on the inner ring. It has been estimated that the combination of these two stresses with Hertzian loading can reduce the fatigue life by 90% in aeroengine bearings [577]. Any tangential tensile stress is detrimental to bearing performance [578]. Aircraft engine bearings are susceptible because they have heavy interference fits, and particularly high rotation speeds. The centrifugal forces associated with these speeds can generate large ![]() GPa) contact stresses between the rolling elements and rings in addition to hoop stresses which make the bearing sensitive to catastrophic failure following damage due to spall formation [324, 303]. This is why, for example, M50NiL is used for the bearing rings rather than M50, since in its case-hardened condition the former has a larger core toughness.
GPa) contact stresses between the rolling elements and rings in addition to hoop stresses which make the bearing sensitive to catastrophic failure following damage due to spall formation [324, 303]. This is why, for example, M50NiL is used for the bearing rings rather than M50, since in its case-hardened condition the former has a larger core toughness.
The calculations of contact stresses could in principle form the basis of methods for predicting failure. Rolling contact fatigue life might be estimated from some combination of models of the nucleation and growth of cracks in fatigue loading. An example [558] of such an approach is presented here with the aim of illustrating the framework; it is appreciated that there are additional complexities which must be accounted for when dealing with real scenarios, but such an approach can nevertheless be stimulating. Actual models used in declaring bearing life are described in section 17.
Uniaxial fatigue tests of smooth samples test initiation and could form the basis for assessing nucleation. The slope of the ![]() versus
versus ![]() Curve (Fig. 56) when testing smooth specimens for fatigue crack initiation, between the limits
Curve (Fig. 56) when testing smooth specimens for fatigue crack initiation, between the limits ![]() (ultimate tensile strength) and
(ultimate tensile strength) and ![]() tends to be a straight line, described as the Basquin law [579]:
tends to be a straight line, described as the Basquin law [579]:
The location of crack initiation is assumed to correspond to the point where the ratio of the maximum shear stress to microhardness is at a maximum, although this cannot be generally true since it is inclusions which initiate cracking in practice. The location of the maximum shear stress and inclusion need not coincide, and a lower stress region containing a weak inclusion may initiate failure.
Having defined the nucleation stage, crack propagation is represented by the Paris law (equation 14) so that a combination of the nucleation and growth models give an equation of the form
| (23) |
This discussion above does not consider the micromechanisms of crack evolution, nor of the crack morphologies. It has been shown in a rather elegant study [581] that the initiation of cracks is governed by the superposition of the local stress field in the vicinity of an inclusion, with the applied contact pressure. It follows that the starting orientation of the crack, assuming that this is determined by the stress field alone as opposed to fracture along features such as prior austenite grain boundaries, will be different from the path taken by the fracture front when it is beyond the influence of the inclusion. The initiation life is defined in this context by the change in the propagation orientation of the crack, and this turns out to be about a tenth of the total rolling contact fatigue life (including some sliding) tests done at realistic Hertzian pressures. The crack orientation at the start tends to be variable since it is the local structure of the inclusion and matrix with dominates the process. The subsequent change in orientation is governed more by the continuum components of the applied stress field and this is more predictable, at some 15 ![]() to the raceway surface. However, this angle can be dramatically modified when the crack encounters residual stress fields in the proximity of the raceway surface. If the circumferential residual stress is sufficiently large and compressive then the subsurface crack may propagate parallel to the raceway without breaking the surface.
to the raceway surface. However, this angle can be dramatically modified when the crack encounters residual stress fields in the proximity of the raceway surface. If the circumferential residual stress is sufficiently large and compressive then the subsurface crack may propagate parallel to the raceway without breaking the surface.
The life of a component is determined by its ability to perform its intended role; when it is no longer able to do this, it is considered to have failed. In the case of ball-bearings such as the one shown in Fig. 71, a failure is considered to occur when the bearing is no longer able to perform rotations or when rotations take place with excessive vibrations and noise. Failure may also occur in a more dramatic manner by fracture through the entire section of a bearing component. Complete failures happen in very few cases because the bearings are stopped when vibrations and noise are detected beyond predetermined thresholds; continued use leads to seizure. Vibration and noise normally arise due to the formation of spalls and pits at the contact surface between the raceway and the balls [582].
![\includegraphics[width=0.98\linewidth]{bearing.eps}](img415.png) |
There are many causes why a component subjected to contact fatigue can fail. The component will be subjected to wear if the lubrication is not appropriate. Indents eventually appear on the contact surfaces if the lubrication contains dust or is not filtered [583]. If the load is too high, seizure will occur, but if all of these are avoided then the only alternative and viable cause of failure is due to the continuous accumulation of damage which can be accelerated by plastic deformation and strain or stress-induced structural changes due to service load, leading eventually to spalling [586, 585, 584]. The useful life is dependent on the stressed volume, alternating shear stress, number of stress repetitions, depth of alternating shear stress and the state of residual stress [587].
Bearings are generally regarded as components which have high surface-integrity and hence the fatigue problems that occur usually are attributed to damage within the steel itself. In 52100 steel quenched and tempered to a hardness of 753HV, the endurance limit on smooth-specimen tests has been determined to be ![]() Shear stress amplitude
Shear stress amplitude ![]() MPa for
MPa for ![]() Cycles [18]. When crack-like features were introduced at the otherwise smooth surface, the crack propagation rates were found to be extremely slow at less than
Cycles [18]. When crack-like features were introduced at the otherwise smooth surface, the crack propagation rates were found to be extremely slow at less than ![]() mcycle
mcycle ![]() .
.
Rolling contact fatigue is a common type of failure encountered in bearings which are well-lubricated so that other mechanisms of damage originating at the contact surface do not determine life. 16 It is influenced by parameters such as contact pressure, material properties, lubricant properties, surface roughness, amount of relative sliding or slip in the contact, microstructure (including retained austenite content), residual stresses and inclusion size and nature [589, 185, 588]. It differs from structural fatigue (bending or torsion) in that the cyclic stress originates in Hertzian contact, when a curved surface rolls over another curved or flat surface under normal load. The mechanism for failure under these circumstances was first proposed by Suh [590]; near-surface plastic deformation leads to the heterogeneous nucleation of voids or microcracks which then grow or connect by a fatigue mechanism [227, 591]; it has also been suggested that the defects may grow in a ductile manner by progressive shear of the surface layer [574]. Once damage is exposed to the surface, material may be removed from the bearing as spalls or other debris, and this in turn can enhance abrasive wear and eventual loss of integrity.
In tests designed to monitor fatigue crack growth, sliding shear at the crack faces is described as mode II loading which is fully reversed ![]() Ratio of minimum to maximum stress during fatigue loading(
Ratio of minimum to maximum stress during fatigue loading( ![]() ) in order to replicate what happens during rolling contact. Stresses applied normal to the crack faces fall into the category of mode I, which is experimentally easier to apply, but is not representative of rolling contact. In fact the mode II shear is superimposed on a compressive stress during rolling contact; tests can be conducted to simulate these conditions by applying both torsion and compression simultaneously to cylindrical samples, and there is limited evidence that the crack morphologies are similar to those observed in rolling contact fatigue [467, 466], although White matter formation (secton 21) seems to be absent. However, there is some evidence of a qualitative correlation between fatigue crack growth rates monitored in mode I loading, and rolling contact fatigue results [592, 218].
) in order to replicate what happens during rolling contact. Stresses applied normal to the crack faces fall into the category of mode I, which is experimentally easier to apply, but is not representative of rolling contact. In fact the mode II shear is superimposed on a compressive stress during rolling contact; tests can be conducted to simulate these conditions by applying both torsion and compression simultaneously to cylindrical samples, and there is limited evidence that the crack morphologies are similar to those observed in rolling contact fatigue [467, 466], although White matter formation (secton 21) seems to be absent. However, there is some evidence of a qualitative correlation between fatigue crack growth rates monitored in mode I loading, and rolling contact fatigue results [592, 218].
Threshold stress intensities ![]() Threshold stress intensity range for crack propagation in shear mode II
Threshold stress intensity range for crack propagation in shear mode II ![]() Threshold stress intensity range for crack propagation in shear mode III
Threshold stress intensity range for crack propagation in shear mode III ![]() and
and ![]() for the shear modes II and III respectively, have been determined by observing non-propagating cracks in cyclic torsion tests (
for the shear modes II and III respectively, have been determined by observing non-propagating cracks in cyclic torsion tests ( ![]() ) and have been found to be in the range 6-20
) and have been found to be in the range 6-20 ![]() (Fig. 72), with not much of a difference between the values for modes II and III [595, 18, 593, 594]. The higher values corresponding to longer cracks in experiments where the applied stress was progressively reduced until the cracks stopped growing; the experiment suffers from the fact that fractures formed at higher stresses have relatively blunt tips which may not propagate as the loading is reduced. This would result in an overestimation of the threshold intensity for the longer crack lengths. Much smaller values of
(Fig. 72), with not much of a difference between the values for modes II and III [595, 18, 593, 594]. The higher values corresponding to longer cracks in experiments where the applied stress was progressively reduced until the cracks stopped growing; the experiment suffers from the fact that fractures formed at higher stresses have relatively blunt tips which may not propagate as the loading is reduced. This would result in an overestimation of the threshold intensity for the longer crack lengths. Much smaller values of ![]() have been found for a similar steel as used in [18] in tests where crack closure was prevented.
have been found for a similar steel as used in [18] in tests where crack closure was prevented.
In an interesting study, Matsunaga et al.[594] discovered that the threshold values of ![]() and
and ![]() depend on the crack size, because debris develops due to the rubbing together of crack faces in the shear mode of deformation. This debris then acts to mechanically interfere with the relative motion of the faces, in effect providing a mechanical interlock of asperities. They described this as an example of a sliding mode of crack closure. The threshold therefore increases as the non-propagating crack becomes larger; the effect persists even in the absence of a compressive stress normal to the crack faces. It has in fact been known for some time that short cracks (dimensions less than those required to justify continuum mechanics) grow faster than long ones in mode I loading due to the absence of crack closure effects [596].
depend on the crack size, because debris develops due to the rubbing together of crack faces in the shear mode of deformation. This debris then acts to mechanically interfere with the relative motion of the faces, in effect providing a mechanical interlock of asperities. They described this as an example of a sliding mode of crack closure. The threshold therefore increases as the non-propagating crack becomes larger; the effect persists even in the absence of a compressive stress normal to the crack faces. It has in fact been known for some time that short cracks (dimensions less than those required to justify continuum mechanics) grow faster than long ones in mode I loading due to the absence of crack closure effects [596].
|
(a)
![\includegraphics[width=0.45\textwidth]{Muramoto.eps}](img421.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{pred111.eps}](img422.png)
|
Failure is usually defined by spalling, which begins with microcracks initiating below the bearing surface, followed by coalescence of multiple microcracks which then reach the surface. The detailed topology of the internally cracked surface depends on factors such as the rolling contact stress, the temperature and any crystallographic texture that develops under the bearing surface during prolonged fatigue [598]. It is found that relative to the rolling direction, the leading edge of the spall is sharper than that which trail s, and there may be further fine-scale damage on the trail ing edge through debris created by spalling [599]. Damage mechanics calculations indicate that the crack initiation part is a small fraction of the total life so that much of the observed scatter may be ascribed to the propagation stage [600].
Although bearing life can be declared in terms of the cycles to the initiation of a spall, impending failure is not noticed until the bearing loses material in the form of spalls which propagate. For this reason it is important to understand the phenomena describing the period between spall initiation and detachment [601]. The need for better metallurgical properties which increase this period would help improve bearing reliability in critical applications.
Bamberger [283] has reviewed the understanding of aeroengine bearing materials. He concludes that although sub-surface nucleated fatigue-spalls are the most understood of phenomena, well-designed and processed bearings made using high-quality steels rarely fail from this mechanism. Fatigue failures in these circumstances usually occur only when the bearing is overloaded, consistent with the fact that accelerated experiments run at unrealistic large stresses also lead to failure in this manner. But in practice, experience suggests that only some 10% of highly-loaded bearings, including those in the aeroengine and rail road applications, fail due to sub-surface initiated fatigue [9]. The vast majority ( ![]() ) of operational failures are attributed to surface distresswhere damage occurs due to pitting, surface fatigue, scoring, debris damage, contamination, plasticity, smearing etc.[283]. Corrosion is a contributing factor to another 10% of failures.
) of operational failures are attributed to surface distresswhere damage occurs due to pitting, surface fatigue, scoring, debris damage, contamination, plasticity, smearing etc.[283]. Corrosion is a contributing factor to another 10% of failures.
The most serious fracture for an aeroengine bearing would be that of the bearing raceway because secondary damage might then compromise the integrity of the engine. In contrast, spalling damage is gradual and can be detected through vibration or other sensors.
The mechanically-induced transformation of austenite during rolling contact fatigue can be beneficial in hardening regions where the stresses or strains are localised. Such transformation may also give rise to beneficial residual stresses (section 4). Many of the experiments probing these phenomena are done at unrealistically large stresses; for example, for contact pressures in excess of 5 GPa, it is reported that a greater retained austenite content is beneficial to the life of 52100 steel [185]. The ![]() life doubled with a doubling in the
life doubled with a doubling in the ![]() Content, although it was noted that the prior austenite grain size was not kept constant in this comparison; neither was the carbon concentration of the martensite. There is other evidence of a beneficial effect of retained austenite on bending fatigue [602], on fatigue crack propagation [603, 604], near threshold crack growth rates and environmentally-assisted cracking [605], fatigue resistance of carburised steel [606] and with respect to rolling contact fatigue [607, 608]. Any such benefit would naturally have to be weighed against other consequences such as a reduced elastic limit [609] or dimensional stability (section 20.8).
Content, although it was noted that the prior austenite grain size was not kept constant in this comparison; neither was the carbon concentration of the martensite. There is other evidence of a beneficial effect of retained austenite on bending fatigue [602], on fatigue crack propagation [603, 604], near threshold crack growth rates and environmentally-assisted cracking [605], fatigue resistance of carburised steel [606] and with respect to rolling contact fatigue [607, 608]. Any such benefit would naturally have to be weighed against other consequences such as a reduced elastic limit [609] or dimensional stability (section 20.8).
Crack nucleation at the surface is not common in rolling contact because of the compressive stress that exists just below the contact regions [610]. It is, however, possible for fatigue cracks to originate from the contact surface in the presence of appropriate stress concentrations or thermal damage, or because of a combination of stresses from rolling contact and bending-type fatigue loading [610]. Surface-initiated spalls due to features such as machining marks are easily identified using fractography because the marks influence the shape of the spall [612, 611]. Fatigue striations near the point of initiation seem to be more readily observed with surface initiated spall than in cases where damage begins deep inside the material [611], possibly because of the greater constraint associated with sub-surface damage. Combinations of rolling contact and sliding can also lead to surface initiation [613] and this is the mechanism common in rail way lines where sliding features more prominently. Such cracks subsequently propagate through the sub-surface zone with the highest mode II shear stress.
Fig. 73shows an admittedly simplified interpretation based on the work in [612]. Furrows caused by machining marks alter the shape of the spall in a distinct manner and hence the connection with the spall is easy to notice. Indents, when they have a smooth shape, can indicate the initiation site, but they may be rough, in which case it is difficult to distinguish between pits and dents unless the former contains some evidence for the mechanism of pit formation, for example in the form of corrosion signals.
![\includegraphics[width=0.98\linewidth]{surface_initiation.eps}](img425.png) |
A complication from surface initiated cracks is that lubricant or corrosive media can penetrate the open crack [614], and transmit the Hertzian contact pressure at the mouth of the crack to underlying crack faces, although the magnitude of the pressure must decrease towards the crack front. The penetration of the lubricant is most effective when there is a combination of sliding and rolling contact which helps to open up the crack mouth [591]. When penetration does occur, the resultant periodic and large pressure pulses at the crack face play an essential role in the propagation of fracture [615]. There would therefore be a particular dependence of failure on the frequency of the pressure pulses and hence the operating conditions. Very high speeds may not give sufficient time for the pressure to be transmitted to the crack front [616]. The crack path itself can be complicated; it can turn up towards the surface or continue propagating away from the surface depending on the local stress states including contributions from any residual stresses [617].
Not much attention has been paid to optimising the toughness of bearing steels. It is known, however, that even surface initiated cracks tend to penetrate the depth of the material when the threshold crack intensity range for fatigue crack growth in mode I is below about 5 ![]() [615].
[615].
It is frequently difficult in post-mortems to distinguish between surface and interior initiated cracks. In general, an oval spall indicates a sub-surface initiated failure whereas a fan shaped spall is taken to indicate surface initiation [573]. But if lubricants play a role in surface-breaking cracks as described above, then Littmann [613] has shown that the appearance of the damage will be quite different Fig. 74. A surface-initiated crack in the presence of a lubricant would exhibit pronounced branching and ill-defined spalls; the fluid pressure increases the tensile mode stress intensity at the crack tip and hence causes it to branch in an orientation normal to the maximum tensile stress [618]. An increase in the severity of crack-branching correlates strongly with a reduction in the ![]() life of bearing steels [619]. The detailed path of the crack can be affected by hoop stresses introduced during press-fitting, which tend to drive the crack towards the bearing bore [324].
life of bearing steels [619]. The detailed path of the crack can be affected by hoop stresses introduced during press-fitting, which tend to drive the crack towards the bearing bore [324].
Surface cracks are also susceptible to any corrosive influence from contaminants within the lubricant. Although such media may not cause significant general attack, their influence can be prominent in the vicinity of the crack tip where the conjoint effect of stress and corrosion can accelerate crack growth [620].
![\includegraphics[width=0.98\linewidth]{Littmann.eps}](img427.png) |
Bearing life is usually declared by conducting rolling contact fatigue tests on full-scale bearings. However, accelerated tests are useful in the assessment of new materials or technologies. Such tests may involve much larger contact stresses than would be experienced in service and hence cannot be used as an indicator of bearing life. Furthermore, the true contact stress will be reduced if the bearing raceway is plastically deformed causing the contact area between the surfaces in rolling contact to increase [622, 621, 623]; in extreme circumstances, a shallow groove forms on the raceway through the plastic accommodation of the rolling element. Empirical correlations exist, for example in the case of M50 bearings, the spalling-limited life in rolling contact at two different Hertzian pressures are related by [570]
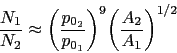 |
(24) |
It is also possible that at the very high loads associated with accelerated testing, the material fails by mechanisms not related to those that arise during service [623], rendering the results useless in assessing bearing life under realistic conditions. The smearing of cracks by plastic deformation is a case which occurs only at abnormal rolling contact stresses.
Bearing quality is often associated with acoustic and vibrational performance because the resulting small oscillatory motions cause wear and material transfer between the abutting surfaces. Fretting occurs when two bodies in contact rub against each other, with the rubbing action described in terms of a contact stress, and the amplitude and frequency of the slip oscillation. When the amplitude is a few micrometers, the oscillations lead to the initiation and propagation of fatigue cracks. Larger amplitudes lead to fretting wear and damage, and the creation of debris that enhances the abrasion. It is this loose and voluminous debris which is the characteristic feature of fretting wear [626]. The problem can be made worse when debris is retained in the affected zone because the fretting surface is much larger than the oscillation amplitude [627]. The parameters that influence fretting include relative humidity, temperature, frequency, the roughness of the surfaces in contact, normal force, displacement amplitude and the number of cycles [628]. The length of the fatigue crack initiated in fretting is thought to be proportional to the width of the contact patch and this is important in determining whether the crack propagates [629]. Some data are illustrated in Fig. 75, showing how weight loss due to fretting corrosion varies with the oscillation frequency and material hardness.
![\includegraphics[width=0.98\linewidth]{Paland.eps}](img431.png) |
Surface damage due to fretting influences rolling contact fatigue by acting as stress concentrators which in turn cause premature spalling. Experiments on M50 steel reveal that fretting wear created using a slip amplitude is 21µm and 10Hz with a Hertzian contact pressure of 1.1GPa can lead to significant reductions in the rolling contact fatigue life measured with a contact pressure of 3.4GPa, as illustrated in Fig. 76[631].
![\includegraphics[width=0.98\linewidth]{fretting.eps}](img432.png) |
A body of evidence has established that the presence of hydrogen in bearing steels leads to a deterioration in mechanical properties, including the resistance to fatigue [634, 633, 635], irrespective of the mode of loading.
Phenomena associated with damage, such as White matter, also become more prominent when cyclic stress is applied in the presence of hydrogen. This is why traces of the decomposition products of lubricant [636], water in the lubricant used in bearings [637] 17 , water created through chemical reactions [135], or exposure to hydrogen sources through other corrosion reactions, can lead to a reduction in bearing life. It has long been known that operating bearings in a hydrogen atmosphere leads to hydrogen embrittlement and extensive surface pitting and flaking [639]. Recent work has shown that if hydrogen present in the atmosphere around a ball bearing then it can be mechanically squeezed into the steel [640]. Hydrogen sulphide ( ![]() ) has a similar effect to hydrogen because it inhibits the recombination of hydrogen atoms at the metal surface [635].
) has a similar effect to hydrogen because it inhibits the recombination of hydrogen atoms at the metal surface [635].
Hydrogen has an undesirable influence on both the 52100 type and stainless steels such as 440C (Table 1) [641]. For reasons which remain a mystery, its penetration into 440C during hydrogen charging is relatively reduced so that the deterioration in fatigue properties is proportionately smaller, Fig. 77a, [635]. One possibility is that the high chromium concentration in 440C retards the diffusion of hydrogen, as the comparison of the diffusion coefficients in a low-alloy ferritic steel (0.09C-0.5Mn wt%) and a ferritic stainless steel (0.26C-14.1Cr-13.Ni-0.4Mn-0.4Si wt%) shown in Fig. 77b, [642].
|
(a)
![\includegraphics[width=0.45\textwidth]{Ciruna.eps}](img434.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Eschbach.eps}](img435.png)
|
It is astonishing that the concentration of hydrogen that leads to perceptible degradation can be as small as 1 part per million, and even this value may represent different forms of hydrogen within the steel. Diffusible hydrogen is that which is in solid solution or is weakly trapped within the steel; it can migrate through the steel and escape into the atmosphere. In order to study the effect of such hydrogen on fatigue, within a time scale which avoids significant loss by diffusion, it is necessary to use high frequency (20kHz) ultrasonic loading. Such tests have been shown to approximate conventional low-frequency push-pull fatigue experiments in samples which are not charged with hydrogen [27], with the results being largely independent of frequency [542]. It is worth noting that very high frequency testing can lead to adiabatic heating, but the temperature excursions can in principle be avoided by specimen design [643] and air-blast cooling.
On the other hand, tests which monitor fatigue crack growth rates show a strong dependence on frequency, with crack advance occurring some 30 times faster in hydrogen charged samples relative to uncharged specimens when tested at 0.2-20Hz, but the difference vanishes when the frequency is increased to 20Hz [644, 645]. It is postulated that this is because hydrogen has time to accumulate at crack tips at low loading frequencies, thus giving rise to slip localisation and a decrease in the plastic zone size at the crack tip [645]. The validity of this argument is confirmed by observations on austenitic stainless steels, where the diffusivity of hydrogen is about three or four orders of magnitude slower than in ferrite, Table 17. It is found that to detect the influence of hydrogen on the fatigue of austenitic steels, the test must be conducted at a very low frequency (0.0015Hz), in order to permit the hydrogen to diffuse to the tips of the propagating cracks [646].
| Steel | Diffusivity / |
| 304 ( |
|
| 316 ( |
|
| 316L ( |
|
| 405 ( |
Fig. 78illustrates some tests on 52100 steel in which tensile specimens were charged with hydrogen and then immediately tested using ultrasonic loading [27]. The distribution of hydrogen within the specimens is not necessarily homogeneous so that the concentrations plotted require interpretation. But it remains valid to suggest that there is a marked deterioration in the fatigue strength in the presence of hydrogen. The fatigue properties recover when the hydrogen is permitted to escape from the steel prior to testing, as illustrated by the single black point on Fig. 78. This confirms in the context of bearings, a generally known fact that it is the diffusible hydrogen that does the damage [647], rather than any that is trapped, for example at interfaces, within the material.
![\includegraphics[width=0.98\linewidth]{diffusible_H_fatigue.eps}](img441.png) |
![\includegraphics[width=0.98\linewidth]{diffusible_inclusions.eps}](img442.png) |
Neglecting the few surface initiated failures, fish-eye cracks initiated in the hydrogen-free sample at alumina or TiN inclusions, or from an unspecified source within the matrix (this could, for example, have originated at the prior austenite grain boundaries given the high phosphorus concentration of the steel used, 0.016 wt%). The effect of hydrogen was to eliminate the matrix failures and increase the proportion of failures at TiN particles. Fig. 79summarises the sources of crack initiation as a function of the diffusible hydrogen concentration. Alumina is responsible for the majority of failures, especially in hydrogen-charged specimens; Matsubara and Hamada [27] attribute this to the development of tensile stresses around the alumina, arising during heat treatment due to differential thermal contraction [648], and the migration of hydrogen to those locations. Notice that the presence of hydrogen in the vicinity of the alumina particles seems to degrade fatigue properties, whereas that trapped in the coherency fields of vanadium and molybdenum carbides leads to an improvement in the resistance to hydrogen-induced static failure [649]. This must be attributed both to the much larger size, lack of toughness and lack of cohesion with the matrix when it comes to alumina particles. The interpretation of stress fields around inclusions is sometimes complicated by the fact that they may not be homogeneous; thus, a sulphide coating on alumina can reduce the stress field [650].
A popular mechanism used to explain the interaction between fatigue and hydrogen is that the latter enhances dislocation plasticity [652, 651] by reducing the barriers to dislocation motion; the velocity at which dislocations move for a given stress therefore increases [653]. This in turn is supposed to lead to localised deformation in the vicinity of the fracture surface, giving the appearance of brittle fracture. Although this interpretation in based on localisedenhancement, macroscopic observations are used to back the argument. For example, Fig. 80shows a tensile test conducted, in which pure iron was subjected to hydrogen charging, and illustrates the large reductions in flow stress that occur when the charging current is switched on. This softening is assumed to promote localised plasticity which in turn stimulates the development of White matter. The localisation is said to occur because the stress field at a crack tip attracts hydrogen which in turn softens the enriched region by facilitating slip [655, 654, 653]. This causes the formation of shallow and sufficiently numerous and microscopic ductile-voids which rapidly link in order to give what appears to be a macroscopically brittle failure. The mechanism of ductile-void formation is not explained, and the number density required to produce an apparently brittle failure is not clear. Hydrogen-induced failure at the austenite grain surfaces is also explained by this ductile mechanism because of a postulated tendency for hydrogen to aggregate there.
![\includegraphics[width=0.98\linewidth]{Jagodzinski.eps}](img443.png) |
The mechanism by which hydrogen is supposed to reduce the barriers to dislocation motion is based on the decoration of the dislocations by hydrogen atoms (rather like Cottrell atmospheres). This in effect reduces the strain field of individual dislocations, so that interactions between neighbouring dislocations diminish. For this mechanism to be effective the dislocations must move sufficiently slowly for the hydrogen to continuously remain bound to the dislocations [656]. In other words, the strain rate for a given dislocation density cannot be large compared with the ability of hydrogen to diffuse with the dislocations. This may explain why the test illustrated in Fig. 81, showing the decreases in flow stress on hydrogen charging, was conducted at such a slow strain rate. It is questionable whether the softening phenomenon applies during the process of rolling contact fatigue with high-frequency cyclic stresses.
The softening of pure iron due to hydrogen is in stark contrast to its well-known effect in embrittling ferrite by raising the ductile-brittle transition temperature, thus promoting cleavage fracture [647]. This effect which seems on the whole to be neglected in the literature on bearing steels. Hydrogen embrittlement leads to a dramatic reduction in ductility and toughness, particularly of strongsteels [657, 556]. Fig. 81a illustrates a typical result where a Fe-0.22C-1.05Mn-0.26Si wt% steel is tested after quenching to martensite and then tempering at 150 ![]() C for 10h, with and without hydrogen charging. Such embrittlement must influence the development and propagation of fatigue damage. There is evidence, for example, that cracking precedes the formation of white-etching matter during rolling contact fatigue in hydrogen-charged 52100 type steel so it could be argued that it is this microscopic fracture which is responsible for the acceleration of damage accumulation mechanisms rather than increased plasticity [658].
C for 10h, with and without hydrogen charging. Such embrittlement must influence the development and propagation of fatigue damage. There is evidence, for example, that cracking precedes the formation of white-etching matter during rolling contact fatigue in hydrogen-charged 52100 type steel so it could be argued that it is this microscopic fracture which is responsible for the acceleration of damage accumulation mechanisms rather than increased plasticity [658].
An alternative interpretation of the role of hydrogen is that it embrittles by weakening atomic bonding to give brittle failure with negligible localised deformation. The hydrogen is therefore associated with a reduction in the cohesive energy of iron [660, 659]. First-principles calculations support a dramatic reduction in cohesive energy in cleavage fracture on the usual ![]() planes of ferrite due to the presence of hydrogen; on the other hand, they do not show that slip becomes easier with the introduction of hydrogen when vacancy generation is neglected [661].
planes of ferrite due to the presence of hydrogen; on the other hand, they do not show that slip becomes easier with the introduction of hydrogen when vacancy generation is neglected [661].
There are results which contradict the softening theory, and show instead that the hardness increases in proportion to the hydrogen content [662]. Similarly, the yield strength has been reported to increase in a hydrogen charged specimen [663]. Hydrogen induced hardening is also reported for 440C martensitic bearing-steel [664]. Attempts have been made to explain the inconsistencies by arguing that the presence of hydrogen limits the number of slip systems that operate, thereby leading to an increase in strength, in nickel alloys [665] and austenitic steel [653]. Observations on austenitic steels show that deformation becomes more heterogeneous with the distance between slip traces increasing in the presence of hydrogen. The proposals, however, remain speculative in the context of ferritic steels where pencil glide dominates deformation.
The observation of microplasticity on the otherwise brittle fracture surfaces of hydrogen-charged specimens is sometimes used to support the claim that the hydrogen enhances plasticity [651]. However, cleavage in iron is well-known to be associated with microscopic plasticity, in that the energy absorbed in creating the free surfaces is far greater than the surface energy per unit area [666].
It is relevant to enquire which mechanism, softening or embrittlement, plays the dominant role in enhancing the rate of fatigue crack initiation or propagation. For steel which is much stronger than pure iron, Fig. 81a shows that the dominant change in property is the loss of ductility on hydrogen charging. Fig. 81b is a plot of the pure iron data on the same scale and it is clear that any softening due to hydrogen is a small effect. Evidence on nickel suggests that hydrogen softening manifests primarily at low stresses, less than about 200 MPa, in a regime where dislocations move slowly [653]. The stresses involved in the rolling contact fatigue of bearing steels are much larger. Hydrogen charged notched tensile specimens of hardened 52100 type steel undergo brittlefracture at a stress much lower than uncharged samples [667].
|
(a)
![\includegraphics[width=0.45\textwidth]{hydrogen_Lee2010b.eps}](img446.png) (b) (b) ![\includegraphics[width=0.40\textwidth]{Jagodzinski_2.eps}](img447.png)
|
An unusual effect has been observed with austenitic stainless steels charged with hydrogen, that beyond a certain concentration, the fatigue properties are enhanced [668]. The amount of martensitic transformation that occurs in the vicinity of the crack tip decreases as the hydrogen concentration is increased. The effect is said to be associated with the hardening of the austenite by hydrogen but the details are not established.
To summarise, the mechanism often assumed to promote rapid fatigue damage in bearing steels, i.e., hydrogen-enhanced local plasticity, should not be considered established since the deductions are largely based on observations of the deterioration of properties following the introduction of hydrogen. Such deterioration could in fact follow directly from the classical embrittlement theory for strong steels, whereby cleavage fracture is promoted at the expense of macroscopic ductility and it is this which leads to the reduction in bearing life.
The total concentration of hydrogen in a steel ![]()
![]() Total concentration of hydrogen in steel is the sum of that which is in solid solution
Total concentration of hydrogen in steel is the sum of that which is in solid solution ![]()
![]() Hydrogen in solid solution and a residue which is trapped at a variety of sites [669]:
Hydrogen in solid solution and a residue which is trapped at a variety of sites [669]:
The free energy change when a dissolved hydrogen atom enters a trap is usually approximated by a binding enthalpy ![]()
![]() Enthalpy which binds hydrogen to a trap, which can be utilised to estimate the fraction of occupied traps [669]:
Enthalpy which binds hydrogen to a trap, which can be utilised to estimate the fraction of occupied traps [669]:
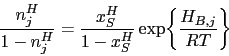 |
(26) |
The tendency for a steel to absorb hydrogen is often studied by cathodically charging small steel specimens with hydrogen, which either remains in solid solution or is trapped. Given time, the former is able to diffuse out of the sample over a period of time at ambient temperature, leaving behind the trapped hydrogen. A programmed temperature furnace connected to a gas chromatograph can then be used to progressively un-trap the hydrogen by thermal desorption as the sample is heated. The escape of the hydrogen occurs at higher temperatures for traps with larger binding enthalpies.
Fig. 82shows two examples of such experiments. In the case of the bearing steel SUJ2 [27], the sample was tested immediately after charging and it was established using a control experiment where the sample was heated at 3 ![]() , that the peak below about 150
, that the peak below about 150 ![]() C is due to the evolution of diffusible hydrogen. Data confirming the attribution of this peak to diffusible hydrogen are available also for lower carbon quenched and tempered steels [556] and for pure iron and eutectoid steels [672]. The actual temperature range over which diffusible hydrogen is released will depend on the heating rate and sample size used in thermal desorption analysis. A useful practical definition of diffusible hydrogen is that which escapes when the steel is left at room temperature for several days [673]. The subsequent smaller peak at temperatures in excess of 350
C is due to the evolution of diffusible hydrogen. Data confirming the attribution of this peak to diffusible hydrogen are available also for lower carbon quenched and tempered steels [556] and for pure iron and eutectoid steels [672]. The actual temperature range over which diffusible hydrogen is released will depend on the heating rate and sample size used in thermal desorption analysis. A useful practical definition of diffusible hydrogen is that which escapes when the steel is left at room temperature for several days [673]. The subsequent smaller peak at temperatures in excess of 350 ![]() C corresponds to the release of trapped hydrogen, although the nature of the traps was not stated.
C corresponds to the release of trapped hydrogen, although the nature of the traps was not stated.
The second steel is not a bearing alloy, and is tested after allowing the diffusible hydrogen to escape from the 8mm diameter samples by holding at 20 ![]() C for 100h [674]. It is heat treated to precipitate fine particles of (V,Mo)
C for 100h [674]. It is heat treated to precipitate fine particles of (V,Mo) ![]() C
C ![]() which through their coherency strain fields are able to trap hydrogen. The peak corresponding to this particular alloy therefore represents only the trapped hydrogen. Similar experiments have shown the tendency for small particles of niobium carbide in steel to form strong traps for hydrogen [675]. There have recently been direct observations using atom probe tomography, of deuterium trapped at titanium carbide particles in steel [676].
which through their coherency strain fields are able to trap hydrogen. The peak corresponding to this particular alloy therefore represents only the trapped hydrogen. Similar experiments have shown the tendency for small particles of niobium carbide in steel to form strong traps for hydrogen [675]. There have recently been direct observations using atom probe tomography, of deuterium trapped at titanium carbide particles in steel [676].
![\includegraphics[width=0.98\linewidth]{hydrogen_evolution.eps}](img465.png) |
In most circumstances, the formation of an isolated spall represents the beginning of the end of useful life. The indent left when a spall forms is repeatedly impacted by the bearing rollers during the operation of the bearing. The leading edge is in general little affected by the passage of the rolling element. Fig. 83shows the development of severe damage as a spall initiated at deliberately introduced stress concentrations propagates by progressive material removal at the leading edge, with damage growing along the rolling direction.
|
(a)
![\includegraphics[width=0.25\textwidth]{spall_propagation_a.eps}](img466.png) (b) (b) ![\includegraphics[width=0.25\textwidth]{spall_propagation_b.eps}](img467.png) (c) (c) ![\includegraphics[width=0.25\textwidth]{spall_propagation_c.eps}](img468.png)
|
The stresses following a single impact are compressive on the surface, with tensile hoop stresses below the surface Fig. 84a,b. The analysis [601] shows that the residual stresses along the surface following three impacts become tensile, reaching values in excess of 2 GPa. Cracks therefore form as illustrated in Fig. 84c and on further impact the cracked region breaks away allowing the spall to propagate [601]. Pitting was initiated at a specific location in the samples shown in Fig. 84using hardness indents to create a local heterogeneity; it is interesting that the same effect can be achieved using a local thermal treatment which changes the microstructure in the vicinity of the heat input [677].
|
(a)
![\includegraphics[width=0.45\textwidth]{Branch_radial2.eps}](img469.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Branch_hoop2.eps}](img470.png) ![\includegraphics[width=0.7\linewidth]{spall_propagation.eps}](img471.png)
|
The toughness of the steel also appears to influence the rolling-contact fatigue life, especially in circumstances where environmental effects through for example, the presence of water in the lubricant can have an adverse effect on the bearing life [20, 678]. It seems that in the 1C-1.5Cr steel, a lower bainitic microstructure can be produced by isothermal transformation to hardness levels which are comparable to those achieved with tempered martensite. It is argued that the greater toughness of lower bainite, when compared with the twinned martensite, leads to better performance in fatigue [20, 679, 218]. The relatively poor toughness of the martensite has been reported to lead to dramatic ultimate fracture whereas the lower bainitic rings failed by slow wear [20]. The heat-treatment used to generate bainite in 52100 steel usually involves transformation for a few hours at about 250 ![]() C, and hence is more expensive than quenching and tempering, which explains why the latter is the chosen method for well-lubricated bearings.
C, and hence is more expensive than quenching and tempering, which explains why the latter is the chosen method for well-lubricated bearings.
![\includegraphics[width=0.98\linewidth]{Bergen_1981.eps}](img472.png) |
There is independent evidence that the modification of 52100 steel with molybdenum, which presumably by mitigating the effects of phosphorus, simultaneously improves toughness and rolling contact fatigue performance [28].
There is some interesting work in the context of the rolling-contact fatigue of back-up rolls used in steel mills [617]. The rolling-contact life of surface initiated cracks scales with the microstructural parameter ![]() Yield strength
Yield strength ![]() bainite sheaf width
bainite sheaf width ![]() where
where ![]() is the yield strength and
is the yield strength and ![]() is the width of the bainite sheaves. The latter controls the effective grain size and hence determines the deflection of cracks across large misorientation boundaries, whereas the former is related to the ease of plasticity.
is the width of the bainite sheaves. The latter controls the effective grain size and hence determines the deflection of cracks across large misorientation boundaries, whereas the former is related to the ease of plasticity.
Failures of high-speed bearings sometimes occur through a phenomenon known as surface distress. There are many mechanisms which result in this kind of damage. Particle-contaminated lubricants can cause raceway indentations, Fig. 86[680]. The partial breakdown of lubricant films and the resulting contact at asperities leads to the formation of small cracks which develop into shallow craters. The damage due to such contact can be reduced if a minimal thickness of lubricant film is maintained to prevent local welding between asperities [681]. There is a distinction made therefore, between elastohydrodynamic lubrication in which the film is sufficiently thick to prevent interference between asperities, and the microscopic version of this which prevents the welding of rough surfaces.
The development of surface damage is therefore not simply a material (steel) issue, but involves the complete system including surface-engineering. For example, the pressure dependence of the shear strength of the lubricant can influence the nature of the pits that eventually develop on the bearing surfaces [682]. The pits are caused by the large pressure gradients that develop close to the bearing surface, and corresponding large shear stress gradients.
![\includegraphics[width=0.98\linewidth]{Nierlich.eps}](img474.png) |
It is useful to emphasise at the outset that full scale experiments which assess the life of a manufactured bearing are not precisely reproducible. Scatter is said to occur when the outcome is different even though an experiment is repeated without changing the control parameters [683]. Repeated rolling contact fatigue tests on bearings exhibit scatter because there are parameters which cannot in practise be reproduced. For example, the probability of finding inclusions in the volume of the test sample that is at the greatest risk. There may exist variations within samples from the same batch of steel, between batches from the same manufacturer, and between steels within the same specification range but supplied from different sources [451]. Real materials are heterogeneous and bearing steels are no exception. The heterogeneities are usually regarded to be randomly distributed and this often forms the basis of models which account for scatter [684].
Any modelling of bearing life must therefore account for the role of statistically distributed defects and yet remain sufficiently simple for practical application.
There are several representations of statistical distributions capable of dealing with repeated measurements which lead to somewhat different outcomes. We shall see that the mathematical form of the Weibull distribution makes it particularly suitable for estimating the service lives of bearings, although log-normal distributions have also been shown to be satisfactory when representing data with low failure probabilities [685].
When a large number of measurements is made of the lifetime of a component and a distribution is plotted, the probability of small or long lives is generally small, with the distribution peaking somewhere in between, Fig. 87. A Weibull probability density function has the form
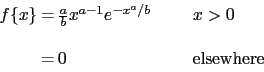 |
(27) |
| (29) |
The versatility of the Weibull distribution to take on the characteristics of other types of distributions is illustrated by setting ![]() , in which case the distribution takes the form of an exponential, with a constant failure rate function, Fig. 87. A constant failure rate is unusual but might arise in special cases where there is regular maintenance.
, in which case the distribution takes the form of an exponential, with a constant failure rate function, Fig. 87. A constant failure rate is unusual but might arise in special cases where there is regular maintenance.
Equation 28is sometimes written with an additional parameter as follows:
The common assumption is that the material tested is heterogeneous with a distribution in the potency of defects. An alternative scenario is that only the extreme defects govern fatigue life and that all such defects have the same severity; the observed dispersion is then attributed to the probability of finding such extreme defects in the stressed volume [688]. There does not seem to have been an attempt to distinguish these models using experimental data, but it is in any case likely that the true dispersion is a consequence both of a distribution in the severity of defects and the probability of these defects lying within the stressed volume. After all, the volume discussed is not homogeneously stressed so it is feasible that a less severe defect in a highly stressed region is as damaging as an extreme defect lying in the less loaded region.
We now see how the Weibull distribution features in the methodologies used to define bearing life.
A definition of the life of a rolling bearing is the number of revolutions before the fatigue-induced detachment of spalls perceptibly influences the noise and vibration characteristics. The common method for estimating the life of bearings was proposed by Lundberg and Plamgren [689], based on a formula which takes account only of load, and is based on Weibull [690].
Equation 30is rewritten here in terms of the fracture stress ![]() of a brittle material as follows:
of a brittle material as follows:
| (31) |
However, there is a difficulty in applying the Weibull equation to rolling contact. The equation gives the static breaking strength assuming that the first crack in a brittle solid leads to a break. This is not the case for bearings where cracks that originate at a depth have to develop in order to break the surface and allow fracture to occur. Lundberg and Plamgren therefore suggested that it is necessary to account for the depth at which the most dangerous stress occurs. They suggested the following functional form for probability of survival given a number of stress-cycles ![]() , material and the stressed volume
, material and the stressed volume ![]() :
:
| (32) |
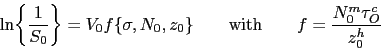 |
(33) |
There are complications to this simple interpretation since ![]() is not always found to be constant, but rather dependent on the Hertzian pressure [622, 621]. When vacuum processing began to be used, it was found that in practice these exponents were measured to be 4 for ball bearings and 5 for roller bearings [517]. Note the
is not always found to be constant, but rather dependent on the Hertzian pressure [622, 621]. When vacuum processing began to be used, it was found that in practice these exponents were measured to be 4 for ball bearings and 5 for roller bearings [517]. Note the ![]() is an estimate based on a finite number of tests, whereas the term
is an estimate based on a finite number of tests, whereas the term ![]() is sometimes reserved for a corresponding life evaluation based on an ``essentially infinite" population, often referred to as a catalogue-rated life [613].
is sometimes reserved for a corresponding life evaluation based on an ``essentially infinite" population, often referred to as a catalogue-rated life [613].
Some of the issues associated with an exponent ![]() which is dependent on load arise from the possible existence of a limiting load below which damage is not perceived for a specified number of fatigue cycles. If the steel concerned exhibits a fatigue limit (as opposed to an endurance limit, section 14) then equation 35has been modified [692, 691] as follows, based on the logic that the effective stress in determining life is now
which is dependent on load arise from the possible existence of a limiting load below which damage is not perceived for a specified number of fatigue cycles. If the steel concerned exhibits a fatigue limit (as opposed to an endurance limit, section 14) then equation 35has been modified [692, 691] as follows, based on the logic that the effective stress in determining life is now ![]() :
:
The original formulation of the Lundberg and Plamgren method was found to be too limiting because it did not contain sufficient parameters to deal with advances in material and associated technologies. that it underestimated the life because it was based on old data. It was therefore phenomenologically modified, by Ioannides et al. [693], to take into account the nature of the material used and the type of lubricant. The expected bearing life ![]() is then
is then
As an example ![]() and
and ![]() for VIM-VAR M50 [696]; in another study,
for VIM-VAR M50 [696]; in another study, ![]() has values of 1, 3 and 6 for material that is air-melted, vacuum induction melted and vacuum induction melted
has values of 1, 3 and 6 for material that is air-melted, vacuum induction melted and vacuum induction melted ![]() vacuum arc refined, respectively [697]. Relationships such as that in equation 37can be modified to account for the presence of hoop stresses due to mechanical fitting of a bearing to a shaft, or to residual stresses built into the steel prior to service [302]. Some typical values of the material and processing factors are shown in Table 18, and there may be other terms related to speed and misalignment effects that influence life [698].
vacuum arc refined, respectively [697]. Relationships such as that in equation 37can be modified to account for the presence of hoop stresses due to mechanical fitting of a bearing to a shaft, or to residual stresses built into the steel prior to service [302]. Some typical values of the material and processing factors are shown in Table 18, and there may be other terms related to speed and misalignment effects that influence life [698].
A processing parameter ![]() is concerned with factors such as melting practice, thermomechanical treatment, hardness and the difference in hardness between the rolling element and raceway.
is concerned with factors such as melting practice, thermomechanical treatment, hardness and the difference in hardness between the rolling element and raceway.
It is worth pointing out that the stress used in these calculations should in principle allow for any residual stresses, loads arising from centrifugal forces and press-fitting [317], and where relevant, thermal stresses due to temperature variations [699]. The role of temperature is complicated by the fact that lubricant properties also change. It is the case that in general, the fatigue properties of common bearing steels deteriorate during operation at temperatures greater than ambient.
| Alloy or Processing | ||
| 52100 | 2.0 | |
| M1 | 0.6 | |
| M2 | 0.6 | |
| M10 | 2.0 | |
| M50 | 2.0 | |
| M50 | 2.0 | |
| VIM | 3 |
Residual stress is that which remains in a body after processing or use [701, 700]: it can be detrimental as it may reduce the tolerance of the material to an externally applied force, such as the load that a structure has to endure. In the context of rolling bearings, the stresses can be beneficial if they are compressive and localised at the surface so as to compensate for contact loads, section 4. Alternatively, they can be detrimental to the manufacturing process in that they cause distortions which can be elastic (`springback' [702]) or permanent, for example ovality, taper or buckling of rings and bending of shafts [703]. Tensile residual stress in general reduces fatigue life, and compressive residual stress improves it, but the effect is via shear stresses and the consequence on life have been expressed empirically as follows:
| (38) |
However, the details of how the residual stress patterns affect the life of components are not easy to assess, because the residual stresses are self equilibrating over a variety of distances and are influenced by a multitude of factors [704]. In an ideal situation a favourable residual stress will superimpose on an elastic stress and this will result in an enhanced fatigue life for a component. In the case of bodies of revolution, such as rings, the residual stresses which need to be taken into account are the tangential and axial components, because the radial stress is generally minor [705].
Residual stress is classified according to the scale over which it self-equilibrates. Long-range stresses (type I) equilibrate over macroscopic dimensions. Type II residual stress equilibrates over a number of grain dimensions. Type III stresses, on the other hand, balance within the grain [701, 700].
Macrostress(type I stress or body stress) can because of heterogeneities associated with mechanical, chemical or thermal operations performed on the body. Chemical changes propagating from the surface to the interior give rise to macrostress. Thermal volume changes induce residual stress if the body is stress-free at the time when a non-uniform temperature distribution subsequently becomes so. Macro residual-stresses can accumulate during cyclic loading, because there will be some plastic deformation, the material will strain harden, its capacity for plastic stress redistribution will decrease and the stress amplitude will rise in spite of the constant amplitude of the load acting upon the structural part [706].
Microstress(types II and III) results from small scale inhomogeneities such as inclusions with thermal expansion coefficients different from that of the surrounding matrix and can be particularly relevant to damage initiation. There are many types of microstresses, due to the grain structure (thermal stresses due to anisotropic thermal expansion of the grains), from the inherent inhomogeneity of deformation process (including stress accompanying martensitic transformation) and microstresses around inclusions [707]. It has been demonstrated that inclusions such as alumina, which have a smaller thermal expansion coefficient than steel, will on cooling from elevated temperatures induce `thermal' tensile stresses in the surrounding matrix [708, 477]; the strain around an alumina particle during quenching of a bearing steel from 850 ![]() C is about
C is about ![]() [709]. The effects are short range and are likely to have the greatest influence on crack nucleation rather than subsequent longer range growth [708]. In contrast, inclusions such as manganese sulphides, which shrink more rapidly that steel, will have weak or debonded interfaces on cooling from high temperatures. Such inclusions effectively provide a free internal surface which becomes susceptible to crack initiation. In fact, a void on its own is a potent site for fatigue crack initiation and a debonded inclusion can be regarded similarly [477]; an inclusion which has not debonded can still be severely detrimental to fatigue initiation if it cracks because it not only makes a small surface available but also provides a concentration of stress. Bearing steels contain many phases and the distribution of microstress is known to be heterogeneous; in 52100 steel the residual stress in retained austenite has been shown to be tensile in nature but compressive within the martensite in a mixture where the latter occupies 0.83 volume fraction of the structure [710]. The relationship between these microstresses and those distributed over much larger scales does not seem to have been explored.
[709]. The effects are short range and are likely to have the greatest influence on crack nucleation rather than subsequent longer range growth [708]. In contrast, inclusions such as manganese sulphides, which shrink more rapidly that steel, will have weak or debonded interfaces on cooling from high temperatures. Such inclusions effectively provide a free internal surface which becomes susceptible to crack initiation. In fact, a void on its own is a potent site for fatigue crack initiation and a debonded inclusion can be regarded similarly [477]; an inclusion which has not debonded can still be severely detrimental to fatigue initiation if it cracks because it not only makes a small surface available but also provides a concentration of stress. Bearing steels contain many phases and the distribution of microstress is known to be heterogeneous; in 52100 steel the residual stress in retained austenite has been shown to be tensile in nature but compressive within the martensite in a mixture where the latter occupies 0.83 volume fraction of the structure [710]. The relationship between these microstresses and those distributed over much larger scales does not seem to have been explored.
Residual stresses in general can be introduced by thermo-mechanical processes such as machining, burnishing, coating, sand blasting and shot peening, which induce short-range residual stress or by heat treatment, rolling, forging, and welding which induce long-range residual stress. Details, such as the medium into which a hot steel may be quenched can have a large influence, both on the sign and magnitude of the residue of forces locked within the component [711].
The stress can develop during the heterogeneous processing of steel due to the volume expansion associated with the transformation from austenite to various body-centred cubic phases [712]. Heat treatment of the material can add to the residual stress. Carburizing induces compression in the hardened surface layers because of the expansion of the lattice by the carbon enrichment; the core resists this expansion thus putting the surface layers in compression [713]. Honing, hard turning and other machining operations in general induce short-range (50-100 µm depth, [168]) compressive residual stress in the component, due to the mechanical deformation of the surface layers being resisted by the undeformed interior [716, 714, 715]. The full residual stress distribution as a function of depth, resulting from gentle grinding has been characterised [717].
There are two categories of grinding, one used for getting to the approximate dimensions using cuts as deeps as 10mm and relatively slow component feed rate, typically 100 µmmmin ![]() . Shallow cuts are in the range 5-100 µm with much greater feed rates
. Shallow cuts are in the range 5-100 µm with much greater feed rates ![]() mms
mms ![]() ) [718]. The former process naturally creates heat and damage which extends to a greater depth within the steel. Grinding induces tension into the surface when the heat generated using alumina or silicon carbide abrasives tempers the structure causing shrinkage relative to the unaffected base material, Fig. 88[724, 720, 722, 723, 719, 721]. If the surface temperature rises sufficiently to cause austenitisation, then the volume expansion due to subsequent martensitic transformation leaves the surface in compression, to be balanced by tensile stresses at a depth where the steel is tempered by the heat. Sub-surface cracks can then form in the tensile region, which eventually may break through the surface [532]. Grinding using a diamond-impregnated wheel, with its greater cutting ability and thermal conductivity, leads to the development of tensile sub-surface stresses akin to machining [725]. The nature of the coolant used during grinding, whether for example, it is a water-based liquid or oil, can lead to a reduction in the tensile residual stress or alter the form of the stress profile as a function of depth [726]. The effect seems to be primarily through the ability of the lubricant to reduce the temperature increase due to grinding; a high-viscosity lubricant is not helpful in this respect.
) [718]. The former process naturally creates heat and damage which extends to a greater depth within the steel. Grinding induces tension into the surface when the heat generated using alumina or silicon carbide abrasives tempers the structure causing shrinkage relative to the unaffected base material, Fig. 88[724, 720, 722, 723, 719, 721]. If the surface temperature rises sufficiently to cause austenitisation, then the volume expansion due to subsequent martensitic transformation leaves the surface in compression, to be balanced by tensile stresses at a depth where the steel is tempered by the heat. Sub-surface cracks can then form in the tensile region, which eventually may break through the surface [532]. Grinding using a diamond-impregnated wheel, with its greater cutting ability and thermal conductivity, leads to the development of tensile sub-surface stresses akin to machining [725]. The nature of the coolant used during grinding, whether for example, it is a water-based liquid or oil, can lead to a reduction in the tensile residual stress or alter the form of the stress profile as a function of depth [726]. The effect seems to be primarily through the ability of the lubricant to reduce the temperature increase due to grinding; a high-viscosity lubricant is not helpful in this respect.
![\includegraphics[width=0.98\linewidth]{Brinksmeier_1982.eps}](img531.png) |
Burnishing is deliberate process in which the surface is permanently deformed, both in order to induce favourable residual stresses and to improve surface finish [727]; it is generally limited to steels which are softer than most bearing steels. However, it is used for 52100 steel in order to mitigate damage due to hard turning. A modern variant of this involves the use of ultrasonic vibrations to actuate a tool through a distance of about 70 µm; the tool impinges on the steel surface to leave it plastically deformed. The process has been shown to induce a large compressive residual stress in the range 500-900 MPa when hardened 52100 steel is treated in this way, to a depth in excess of 240m [728]. The rolling contact fatigue life has been found to be much improved when a comparison is made against the same material in its ground state for tests conducted at contact stresses in excess of 4GPa. The technique seems to be in its early stages of development and is being investigated in a number of contexts involving the enhancement of fatigue life [731, 730, 729]. It is even argued that the microdimples introduced on the steel surface help trap lubricant and thus result in a reduction of the friction coefficient associated with the Stribeck curve (section 27) to be reduced for all values of the specific film thickness ratio ![]() [732, 733]. Lubricant supplied by indents which are some 2-4 µm deep lead to an increase in the lubrication film thickness [734].s
[732, 733]. Lubricant supplied by indents which are some 2-4 µm deep lead to an increase in the lubrication film thickness [734].s
Machining-induced stresses, whilst important, may not have an overriding influence on sub-surface initiated rolling contact fatigue since the location of the damaging shear stresses is usually at greater depths. Under normal machining circumstances, i.e.with tools which are not excessively worn and have reasonable feed and cutting rates, the stress profile that develops is illustrated schematically in Fig. 89. Such a profile can apparently be predicted quantitatively using finite element modelling [183, 735]. In some innovative work on 52100 steel, the method has been used first to create a dataset of the parameters characterising the stress, which then form the basis of a neural network model linking the profile to material, cutting conditions and tool geometry [736]. This final model can be used to discover the conditions appropriate for desired distributions of residual stress as function of steel hardness, tool tip-radius, cutting speed, and rake angle. The method apparently has reasonable accuracy although it is not clear whether, within the limits of uncertainties, that there should be a unique relationship between the manufacturing parameters and residual stress profile. In inverse problems like this it is often the case that the same output can be reproduced using different sets of inputs [737, 738].
![\includegraphics[width=0.98\linewidth]{Umbrello.eps}](img532.png) |
The simple explanation of why a residual stress develops within a bearing raceway is that the deformation due to rolling contact is heterogeneous. There is a volume of material located under the surface which experiences the maximum shear stress. It therefore deforms and pushes against its surroundings which are less stressed. This puts that volume under compression. The question arises as to why this stress is important in determining life if it is compressive. The answer is that the stress is a consequence, not the cause of microstructural damage resulting from localised deformation. It is this damage that eventually nucleates fracture.
The residual stress patterns usually found beneath the raceway of new and used bearings are illustrated in Fig. 90; only the tangential stress is plotted as a function of the depth below the surface - it is necessary in principle to represent the stress as a tensor consisting of six independent components but only the tangential and axial components are in practice found to be significant [565] 18 . The characteristic feature for a new bearing is the large compressive stress in the close proximity of the surface, resulting from the finishing process; this stress is not changed during the running of the bearing [314]. The magnitude of the stress then decreases with depth, gradually levelling around zero [739, 111]. The depth beneath the raceway where the maximum residual stress is recorded varies as a function of bearing geometry [740] but it is difficult to be precise given additional dependencies on load and temperature [741, 598].
The stress pattern and its evolution as illustrated in Fig. 90is a consequence of localised deformation in the subsurface volume with displacements estimated to be less than 5 ![]() m, and correlates with the development of structural and crystallographic changes in the affected regions [598]. The magnitude of the residual stress correlates with the contact pressure but saturates for very large pressures (
m, and correlates with the development of structural and crystallographic changes in the affected regions [598]. The magnitude of the residual stress correlates with the contact pressure but saturates for very large pressures ( ![]() MPa) [742]. These issues can of course be complicated by the presence of retained austenite which when induced to transform into martensite alters the pattern of stresses via the change in density. [743]. However, the role of retained austenite in steels such as 52100 is likely to be confined to the initial loading cycles during which it is induced to decompose.
MPa) [742]. These issues can of course be complicated by the presence of retained austenite which when induced to transform into martensite alters the pattern of stresses via the change in density. [743]. However, the role of retained austenite in steels such as 52100 is likely to be confined to the initial loading cycles during which it is induced to decompose.
![\includegraphics[width=0.98\linewidth]{cyc.eps}](img535.png) |
For the used bearings, as shown in Fig. 90, the compressive residual stress peaks at a depth between 0.1 and 0.5 mm with increasing cycles, the depth apparently coinciding with that of the maximum shear stress; the position of the latter naturally changes as the state of residual stress develops [744, 111, 598].
The distribution of tangential stress as a function of the type of heat-treatment in new bearing rings is illustrated in Fig. 91. It is not clear why the bainitic ring maintains a compressive stress to a much larger depth.
![\includegraphics[width=0.98\linewidth]{Hengerer_1993b.eps}](img536.png) |
The carbon potential of the atmosphere used during heat-treatment at elevated temperatures also influences the state of stress left in the steel following quenching and tempering. The value of the potential relative to the chemical composition of the steel determines whether the steel surface becomes enriched or depleted in carbon. A low carbon potential leads to the decarburisation of the surface and hence the development of tensile residual stress [747, 746], whereas the opposite occurs when the carbon potential is high for the steel concerned. When there is no carbon-enrichment, the residual stress is zero, as illustrated in Fig. 92. Tensile stresses at the surface are obviously detrimental to subsequent fatigue performance but can also lead to quench-cracking [748].
![\includegraphics[width=0.98\linewidth]{carbon_potential.eps}](img537.png) |
The changes in stress patterns illustrated in Fig. 92for 52100 steel are typical of through hardened bearing steels including those for aerospace applications, for example M50 [291] but not so for the case hardened alloys such as M50 NiL (Fig. 136) where the bearing begins with a built in compressive tangential-stress distribution which penetrates deep below the surface. This latter distribution remains compressive even after prolonged service, with clear benefits to fatigue resistance [291]. It is in this context important to realise that the stress pattern that develops in through-hardened bearings during service, although compressive, is a reflection of the accumulation of damage, whereas that induced through surface treatments such as case-hardening is present prior to service and is benign. Attempts have been made in the past to overload through-hardened bearings prior to normal service in hope that the resulting sub-surface compressive stresses can be beneficial but this neglects the damage that is associated with the accumulation of such stresses.
Induction heat-treatment is likely to become the process of choice when it comes to the surface hardening of bearings, because it can result in considerable cost and time advantages. We focus here on the relationship between bearing-steel composition and the stress profile that results on induction heat-treatment. Fig. 93shows the residual stress as a function of depth following the induction hardening and low-temperature tempering of two steels: ShKh4, ShKh15G (Table 1), with the latter alloy possessing a greater hardenability. The original paper [21] does not provide an interpretation of the results, but they can be rationalised once it is appreciated that the core of the low-hardenability steel was unaffected by the induction treatments, whereas alloy ShKh15G became through hardened.
If only the surface becomes austenitic and then transforms into martensite then the resulting expansion leaves it in a state of compression. However, if the whole sample becomes austenitic and subsequently transforms into martensite, then the expansion of the late-transforming core leaves the surface in a state of tension.
![\includegraphics[width=0.98\linewidth]{Pchelkina.eps}](img538.png) |
It is possible to induce favourable residual stresses within a bearing by overloading the raceway for a number of cycles at a high contact stress ( ![]() -
- ![]() GPa) in order to induce a small amount of plastic deformation [589, 749], Fig. 94. This is prior to the bearing entering service where it experiences much lower contact stresses over millions of cycles and the process has been shown to result in an enhanced rolling contact fatigue life in accelerated tests conducted with
GPa) in order to induce a small amount of plastic deformation [589, 749], Fig. 94. This is prior to the bearing entering service where it experiences much lower contact stresses over millions of cycles and the process has been shown to result in an enhanced rolling contact fatigue life in accelerated tests conducted with ![]() GPa. It is argued that this prestressing involves a relatively small number of loading cycles and hence does not lead to significant microstructural damage of the kind associated with long term service, for example in the form of White matter. It is noteworthy that the prestressing operation did not result in a deterioration of the roughness in the raceway. Experiments suggest that in accelerated tests, the rolling contact fatigue performance is better following prestressing [749]. However, it is important to note that the difference in the measured residual stresses in prestressed bearings and those which have not been subjected to this treatment becomes insignificant after a period in service which is shorter than the bearing life [749]. The value of prestressing is not therefore obvious.
GPa. It is argued that this prestressing involves a relatively small number of loading cycles and hence does not lead to significant microstructural damage of the kind associated with long term service, for example in the form of White matter. It is noteworthy that the prestressing operation did not result in a deterioration of the roughness in the raceway. Experiments suggest that in accelerated tests, the rolling contact fatigue performance is better following prestressing [749]. However, it is important to note that the difference in the measured residual stresses in prestressed bearings and those which have not been subjected to this treatment becomes insignificant after a period in service which is shorter than the bearing life [749]. The value of prestressing is not therefore obvious.
![\includegraphics[width=0.98\linewidth]{Cretu.eps}](img541.png) |
Ultrasonic testing can have a major advantage in terms of the volume of material examined in order to characterise the dispersion of inclusions [750]. The inclusion size-range appropriate for this technique is illustrated in Fig. 95. The optical emission spectroscopy method is essentially a surface method because only a small volume of material is interrogated, Fig. 96[751].
![\includegraphics[width=0.98\linewidth]{Umigame3.eps}](img542.png) |
![\includegraphics[width=0.98\linewidth]{Meyer_2007.eps}](img543.png) |
This relies on the attenuation of X-rays as they pass through the sample; features within an optically opaque sample can be revealed in three-dimensional form if their ability to absorb X-rays is different from that of the steel. Such differences in absorption can arise from variations in density or chemical composition. The X-rays pass through the sample of interest and images are collected from a variety of orientations; these are then reconstructed into a three-dimensional representation. Image processing software can be used to eliminate the matrix and show the shape of the inclusions in isolation. Elongated strings of inclusions which undulate in three dimensions would appear as isolated segments in two-dimensional sections.
Using this technique, it has, for example, been possible to interrogate a steel sample (0.5mm thick) taken from a fractured specimen, to understand the formation and linkage of voids to a resolution of a few m [752]. There are also some remarkable three-dimensional perspectives of inclusion and inclusion clusters in 52100 type steel [684].
Although classified as a non-destructive technique, samples do have to be machined out from an engineering component to a size which is transparent to the X-rays used. The sample itself is of course not affected by the X-irradiation.
This is a destructive technique. Metallographic sections are examined as a function of depth in order to reconstruct the three-dimensional form of features such as inclusions or cracks. Automated procedures have been developed in which the ultrasonically vibrating cutting devices are able to control the depth of machining to about 0.5m while maintaining a mirror finish [753]. As a result two-dimensional images with a resolution of 1m can be collected using optical microscopy directly on the machined surface, without further metallographic preparation needed. The resulting images of inclusions in bearing steels are revealing in terms of the sharpness of their edges and planar morphologies [753].
A reliablepopulation of bearings is one which will statistically fulfill an ![]() life expectation and not suffer from an unexpectedly large number of failures at small fractions of that life. The
life expectation and not suffer from an unexpectedly large number of failures at small fractions of that life. The ![]() fatigue limited life often scales systematically with macroscopic measures related to inclusions, for example the overall oxygen concentration, as illustrated in Fig. 97. This is because it depends mainly on the smaller (
fatigue limited life often scales systematically with macroscopic measures related to inclusions, for example the overall oxygen concentration, as illustrated in Fig. 97. This is because it depends mainly on the smaller ( ![]() m size) and more uniformly dispersed inclusions within the steel. The observed scatter in plots such as that illustrated in Fig. 97is attributed to the fact that the size distribution of inclusions can be different for a given oxygen concentration [118].
m size) and more uniformly dispersed inclusions within the steel. The observed scatter in plots such as that illustrated in Fig. 97is attributed to the fact that the size distribution of inclusions can be different for a given oxygen concentration [118].
![\includegraphics[width=0.98\linewidth]{Unigame.eps}](img546.png) |
Unexpected failures in bearings are often due to the presence of exceptionally large inclusions present in critical locations, i.e.,the volume of material obtained on multiplying the Hertzian contact are between a rolling element and the inner race, and the depth of the region experiencing 90% of the shear stress. To characterise cleanliness in such circumstances requires a focus on the largest inclusions, which because of their rarity are also the most difficult to detect using standard techniques.
Extreme value statistics are based on the measurement of the distribution of inclusions which exceed a defined threshold size, rather than the entire distribution which may include fine, innocuous inclusions. If a field of view is inspected during measurements of inclusion sizes, then only those exceeding the threshold size are counted to form the distribution. The aim is to accurately represent the tail of the distribution of all inclusions. The subject has been reviewed recently [754] where the seminal work of Murakami and co-workers where estimates of the maximum size of inclusions in a large volume of strong steel are related to their fatigue behaviour.
Little attention has been paid to the fact that inclusions and their distributions in bearing steels tend to be anisotropic, particularly when the components of the bearing are mechanically worked into shape at some stage in their manufacture. It is known that the fatigue properties, as represented in ![]() -
- ![]() or rolling contact experiments, vary with test orientation [755]. Ma and co-workers have assessed this variation by correlating the projected area presented by inclusions on a particular section of the steel, against the fatigue life measured by stressing in a direction normal to that section [756]. This makes physical sense because the quantity of inclusion/matrix interface must be proportional to the number density of fatigue crack initiation sites. The ``fatigue limit"
or rolling contact experiments, vary with test orientation [755]. Ma and co-workers have assessed this variation by correlating the projected area presented by inclusions on a particular section of the steel, against the fatigue life measured by stressing in a direction normal to that section [756]. This makes physical sense because the quantity of inclusion/matrix interface must be proportional to the number density of fatigue crack initiation sites. The ``fatigue limit" ![]() Stress corresponding to fatigue limit in
Stress corresponding to fatigue limit in ![]() -
- ![]() tests
tests ![]() is found to vary with the projected area of inclusions as follows:
is found to vary with the projected area of inclusions as follows:
![\begin{displaymath} \sigma_w \propto \frac{{\rm HV+120}}{A_P^{\frac{1}{10}}} \ti... ...erline \sigma]}\biggr)^{0.226+10^{-4}{\rm HV}}\qquad {\rm MPa} \end{displaymath}](img548.png) |
(39) |
Early tests on M2high-speed steels (Table 1) revealed that the presence of retained austenite is detrimental to the fatigue performance of ball bearings, although the mechanism of this effect was not resolved [451]. An opposite effect is reported for the 52100 type steels, where the austenite enhances contact fatigue performance of steel balls [743], when a bearing operates in contaminated lubrication [79, 32], and in the context of carburised gear components [757].
There are suggestions based on modelling that any amount of austenite leads to a deterioration in fatigue performance because the volume expansion accompanying its transformation introduces localised stresses [758, 759]. However, the model is somewhat simplistic in that transformation plasticity is not in reality limited to volume change and furthermore, any martensite that is induced during fatigue should act to relieve local stresses through variant selection [761, 760]. The assumption that the transformation strain is limited to the effect of the density change on martensite formation is not a true reflection of stress-induced transformation as is assumed in these models. Indeed, it has been demonstrated that retained austenite leads to cyclic hardening through transformation, and enhances the development of a mean compressive stress [606, 182]. The effect is said to scale with the amount of austenite, especially when the steel concerned is intrinsically brittle.
To summarise, retained austenite is an important phase in common bearing steels which are based on a predominantly martensitic microstructure. Whereas it is definitely established that the dimensional changes that occur when it transforms can compromise the mechanical fit of the bearings against its shaft, there are contradictory studies on its role in determining the fatigue properties of bearing steels. It is useful therefore to look at some of its fundamental characteristics. The dimensional stability issue is in any case most important in the aerospace industry where bearings are press-fitted on to shafts and where the very high rotation speeds lead to elastic expansion of the rings; the literature does not indicate this is a generic problem in most engineering applications.
It is worth noting at the outset that the vast majority of reported retained austenite measurements do not quote uncertainties, which can be large if the sample preparation leaves the surface in a plastically deformed state [762], because conventional X-rays penetrate at most to a depth of 10m into the steel. The number of diffraction peaks used in the calculation of the phase fraction can dramatically influence the outcome [763]. There will be real variations as a function of depth if the material is not homogeneous; for example, measurements based on sound velocities, which cover larger volumes, can give substantially different retained austenite content than determinations using X-rays [764].
The retained austenite content of hypereutectoid steels naturally varies with the austenitisation temperature ![]() which in practice is less than the
which in practice is less than the ![]() temperature of the alloy, Fig. 98a. It is worth emphasising that it is not just
temperature of the alloy, Fig. 98a. It is worth emphasising that it is not just ![]() which determines the carbon concentration of the austenite, since rate at which carbides dissolve also depends on factors such as the size distribution of spheroidised carbide present in the microstructure prior to heating, and this can in turn influence the retained austenite content on quenching. [247]. Further data are illustrated in Fig. 98b which shows the austenite content for untempered specimens. When dimensional stability due to the decomposition of retained austenite during service is an issue, then the phase can be minimised by using an appropriate tempering heat treatment. An appropriate choice of austenitisation and tempering conditions can completely remove any retained-austenite in 52100 steel without compromising the hardness [765].
which determines the carbon concentration of the austenite, since rate at which carbides dissolve also depends on factors such as the size distribution of spheroidised carbide present in the microstructure prior to heating, and this can in turn influence the retained austenite content on quenching. [247]. Further data are illustrated in Fig. 98b which shows the austenite content for untempered specimens. When dimensional stability due to the decomposition of retained austenite during service is an issue, then the phase can be minimised by using an appropriate tempering heat treatment. An appropriate choice of austenitisation and tempering conditions can completely remove any retained-austenite in 52100 steel without compromising the hardness [765].
Tempering leads to a dramatic reduction in the quantity of retained austenite (Fig. 98). On the one hand there is the partitioning of carbon from supersaturated martensite into the retained austenite which should make the austenite more stable [766], but on the other hand, the austenite can in principle decompose into bainite as long as the tempering time is sufficiently large [769, 767, 768]. Whether bainite actually forms as the retained austenite in bearing steels decomposes remains to be demonstrated because it is possible that existing martensite-austenite interfaces move concurrently with the precipitation of carbides [770, 771]. Comprehensive data on the kinetics of austenite decomposition in the 52100 type steel as a function of manganese concentration and tempering temperature are reported in [772].
|
(a)
![\includegraphics[width=0.4\textwidth]{Beswick_retained.eps}](img551.png) (b) (b) ![\includegraphics[width=0.50\textwidth]{Banerjee.eps}](img552.png)
|
Refrigeration at sub-zero temperatures does not have much of an effect on reducing the amount of retained austenite in samples of 52100 steel which have been quenched andtempered, Table 3. The ability of the austenite in these tempered samples to resist decomposition during sub-zero cooling is probably associated with the partitioning of some carbon from the martensite into the austenite during the tempering heat treatment [774], which would have the effect of reducing its martensite-start temperature. There is direct evidence for such an effect in other steels [775]. Indeed, the sub-zero treatment of untempered martensite in 52100 steel does lead to a substantial reduction in ![]() , Table 19[91], presumably because the carbon has not been partitioned into the austenite. Furthermore, ageing the steel at room temperature prior to refrigeration increases the stability of the austenite [776, 777], as does a reduction in the rate at which the steel is quenched to martensite [778, 779]. The former effect is illustrated in (Fig. 99). Carbon can diffuse from martensite at temperatures well below room temperature [781, 780]. As discussed in the following paragraph, the stability of the retained austenite is found to be consistent with theory when the martensite-start temperature is known even for tempered specimens. An alternative interpretation of the influence of tempering on the stability of the retained austenite is that it reduces microstresses within the sample and in that way stabilises the austenite to transformation during refrigeration.
, Table 19[91], presumably because the carbon has not been partitioned into the austenite. Furthermore, ageing the steel at room temperature prior to refrigeration increases the stability of the austenite [776, 777], as does a reduction in the rate at which the steel is quenched to martensite [778, 779]. The former effect is illustrated in (Fig. 99). Carbon can diffuse from martensite at temperatures well below room temperature [781, 780]. As discussed in the following paragraph, the stability of the retained austenite is found to be consistent with theory when the martensite-start temperature is known even for tempered specimens. An alternative interpretation of the influence of tempering on the stability of the retained austenite is that it reduces microstresses within the sample and in that way stabilises the austenite to transformation during refrigeration.
![\includegraphics[width=0.98\linewidth]{Fletcher_1948.eps}](img557.png) |
 |
It should be emphasised at the outset that the measurement of retained austenite content requires careful sample preparation. This is because X-rays do not generally penetrate more than 10m into steel so that any local deformation of the surface will change the quantity of austenite and the resolution of diffraction information [773]. As a result there are large variations reported when identical samples are analysed by different laboratories [783]. Samples should therefore be chemically polished or electropolished prior to being subjected to diffraction.
The fraction of austenite ![]() that remains untransformed in an otherwise martensitic steel can in principle be calculated using the Koistinen and Marburger equation [712]:
that remains untransformed in an otherwise martensitic steel can in principle be calculated using the Koistinen and Marburger equation [712]:
![\includegraphics[width=0.98\linewidth]{Beswick_1984.eps}](img569.png) |
There are nevertheless difficulties in applying this method to bearing steels for two reasons. First, it is the carbon concentration in solid solution that determines the martensite-start temperature, whereas most bearing alloys are austenitised at a temperature which leaves some cementite particles undissolved. It cannot be assumed that the time at the austenitisation temperature is sufficient for the fraction of cementite to correspond to equilibrium [106]. The role of the microstructure prior to austenitisation is clear from the work of Stickels [182]; Table 4shows how the retained austenite content is sensitive to both the austenitisation conditions and the initial microstructure. The pearlitic cementite is finer in scale, and presumably does not contain the equilibrium concentration of, for example, chromium, that the spheroidised cementite should. Therefore, it is less stable during austenitisation and leads to a larger amount of retained austenite. The kinetics of carbide dissolution during austenitisation, and hence the martensite-start temperature of the austenite will depend on whether the steel was hot or cold deformed prior to the hardening heat-treatment.
| Initial microstructure | Austenitisation treatment | % |
| Spheroidised carbides in ferrite | 840 |
8 |
| Spheroidised carbides in ferrite | 840 |
12 |
| Pearlite | 840 |
17 |
| Spheroidised carbides in ferrite | 927 |
23 |
| Pearlite | 927 |
30 |
Another problem in attempting to estimate ![]() for a carburised case is that the concentration of carbon is then unlikely to be constant as a function of depth. In a study where a 6mm diameter sample was through-carburised to 1.1 wt% carbon, and confirmed to have a homogeneous microstructure,
for a carburised case is that the concentration of carbon is then unlikely to be constant as a function of depth. In a study where a 6mm diameter sample was through-carburised to 1.1 wt% carbon, and confirmed to have a homogeneous microstructure, ![]() was measured to be 0.35 [35]. The calculated
was measured to be 0.35 [35]. The calculated ![]() temperature is then
temperature is then ![]() C, which in conjunction with equation 40indicates incorrectly that the sample would be fully austenitic at ambient temperature. To obtain the correct value of
C, which in conjunction with equation 40indicates incorrectly that the sample would be fully austenitic at ambient temperature. To obtain the correct value of ![]() , it would be necessary for the martensite-start temperature to be about 120
, it would be necessary for the martensite-start temperature to be about 120 ![]() C. When the same material was cooled to
C. When the same material was cooled to ![]() C,
C, ![]() was measured to be 0.14 whereas an
was measured to be 0.14 whereas an ![]() of 120
of 120 ![]() C would leave only a fraction 0.03 of the austenite untransformed.
C would leave only a fraction 0.03 of the austenite untransformed.
The two observations can be reconciled if it is assumed that the sample has a heterogeneous distribution of carbon so that the initial martensite which forms on cooling to ambient temperature is from the low concentration regions, so that the remaining higher carbon austenite will better resist transformation on cooling to a liquid nitrogen temperature.
There is some evidence that the ultrasonic stressing up to 270 MPa of hardened 52100 type steel during tempering leads to an accelerated decrease in the retained austenite content [788]; the original work did not consider whether this is some peculiar effect due to the ultrasonic cycling of stress or simply a stress-induced transformation of retained austenite. However, Fig. 101shows that the phenomenon is most prominent at the higher tempering temperatures, where contrary to the trend, the influence of stress alone would be smaller because of the increase in the thermodynamic stability of the austenite [790, 789]. It is argued that the mechanism involves the highly localised generation of heat at lattice perturbations [788], but how this relates specifically to retained austenite decomposition remains unclear. A useful experiment might involve the repetition of the experiments using monotonically stressed samples.
![\includegraphics[width=0.98\linewidth]{Puskar_1973.eps}](img572.png) |
Bearing steels in the 52100 category are often quenched into warm oil at 50 ![]() C, primarily in order to mitigate thermal shock and its consequences. The retained austenite present after the untempered-steel cools to ambient temperature can be induced to transform further into martensite by sub-zero cooling. However, it has been pointed out that this sometimes leads to a deterioration in toughness and fatigue resistance [791, 792], presumably because of microcracking within the virgin martensite.
C, primarily in order to mitigate thermal shock and its consequences. The retained austenite present after the untempered-steel cools to ambient temperature can be induced to transform further into martensite by sub-zero cooling. However, it has been pointed out that this sometimes leads to a deterioration in toughness and fatigue resistance [791, 792], presumably because of microcracking within the virgin martensite.
In order to avoid this, it is found that the retained austenite content is reduced when the components are, after oil quenching, rinsed immediately in water at 15-20 ![]() C. The water rinsing leads to an initial reduction in the content of austenite, but the results in Fig. 102do not show other significant differences in the kinetics of decomposition during isothermal heat treatment. Given this, it is not clear why the water rinsed samples are claimed to be more dimensionally stable.
C. The water rinsing leads to an initial reduction in the content of austenite, but the results in Fig. 102do not show other significant differences in the kinetics of decomposition during isothermal heat treatment. Given this, it is not clear why the water rinsed samples are claimed to be more dimensionally stable.
![\includegraphics[width=0.98\linewidth]{Hengerer_1988.eps}](img573.png) |
There are two aspects to the mechanical behaviour of retained austenite, its susceptibility to ordinary plastic deformation, and secondly to stress- or strain-induced martensitic transformation. There is little information on the former. However, in an elegant study, Zaccone and co-workers [602, 609] demonstrated that the austenite in 52100 type steel is relatively soft and hence in the composite microstructure, undergoes microscopic plastic deformation during the early stages of straining, resulting in an overall reduction of the elastic limit. The elastic limit decreases as the amount and size-scale of retained austenite is increased. Notice that these observations are in contrast to the so-called TRIP-assisted steels where the finer retained austenite contains a much greater carbon concentration and hence is harder than the surrounding bainitic ferrite [203].
The second aspect of the stability of the retained austenite relates to both thermodynamic and kinetic aspects of diffusionless transformation. Martensite is triggered when the chemical free energy change ![]() for the transformation of austenite to ferrite without a composition change achieves a critical value
for the transformation of austenite to ferrite without a composition change achieves a critical value ![]() , i.e.,when a sufficiently large undercooling is reached below the equilibrium transformation temperature [57, 793, 794]. The temperature at which martensite first forms is designated
, i.e.,when a sufficiently large undercooling is reached below the equilibrium transformation temperature [57, 793, 794]. The temperature at which martensite first forms is designated ![]() .
.
Since martensitic transformation causes a deformation, it can also be stimulated by applying an external stress which supplements the chemical component. The additional free energy due to the interaction of the applied stress and the shape deformation of martensite is the mechanical free energy ![]() [795, 796]. The transformation from austenite can therefore be stimulated at a temperature above
[795, 796]. The transformation from austenite can therefore be stimulated at a temperature above ![]() , simply by applying a stress. The mechanical free energy due to the interaction of the stress with the shape deformation is given by [795]:
, simply by applying a stress. The mechanical free energy due to the interaction of the stress with the shape deformation is given by [795]:
What all this means is that when a bearing steel containing retained austenite is put into service, the imposed stresses may stimulate martensite to form. Fig. 103shows the plastic strain recorded when a quenched and tempered molybdenum-modified 52100 steel (referred to as `MMM' in Table 1), containing about 12% ![]() , is subjected to a uniaxial load in compression or tension [29]. The strains recorded are less than the 0.2% used to define a proof strength and it is noteworthy that they occur at rather small stresses. The strains illustrated are largely due to the transformation of retained austenite, and are smaller in compression than in tension; this is expected from equation 41because the
, is subjected to a uniaxial load in compression or tension [29]. The strains recorded are less than the 0.2% used to define a proof strength and it is noteworthy that they occur at rather small stresses. The strains illustrated are largely due to the transformation of retained austenite, and are smaller in compression than in tension; this is expected from equation 41because the ![]() is negative in compression and hence opposes the positive dilatational component
is negative in compression and hence opposes the positive dilatational component ![]() (Table 5).
(Table 5).
For the data illustrated in Fig. 103the magnitude of ![]() at
at ![]() is 1415Jmol
is 1415Jmol ![]() . That of
. That of ![]() for a uniaxial tensile stress of 500 MPa can be estimated to be a maximum of 430Jmol
for a uniaxial tensile stress of 500 MPa can be estimated to be a maximum of 430Jmol ![]() and when this stress is uniaxial compression, 290Jmol
and when this stress is uniaxial compression, 290Jmol ![]() . The mechanical driving force is therefore rather small compared with the chemical component so it is unlikely that there would be strong variant selection [789]; in such circumstances, the transformation strain will be close to isotropic and will reflect the volume change component only. In both cases, the mechanical driving force assists the formation of martensite because the shear component of strain overwhelms the much smaller dilatational term.
. The mechanical driving force is therefore rather small compared with the chemical component so it is unlikely that there would be strong variant selection [789]; in such circumstances, the transformation strain will be close to isotropic and will reflect the volume change component only. In both cases, the mechanical driving force assists the formation of martensite because the shear component of strain overwhelms the much smaller dilatational term.
It has been argued, on the basis of austenite contents measured using two different X-ray line intensities ( ![]() and
and ![]() planes), that during the application of stress, the rate of austenite transformation is a function of the crystallographic orientation of the austenite grains. While it is true that there must be some dependence of the influence of stress on the austenite orientation [789], the reason for obtaining different
planes), that during the application of stress, the rate of austenite transformation is a function of the crystallographic orientation of the austenite grains. While it is true that there must be some dependence of the influence of stress on the austenite orientation [789], the reason for obtaining different ![]() for the 002 and 022 diffraction peaks may well be the existence of texture, in which case it is not appropriate to calculate two different retained austenite contents, but rather to take the weighted average intensities of different peaks and estimate a single
for the 002 and 022 diffraction peaks may well be the existence of texture, in which case it is not appropriate to calculate two different retained austenite contents, but rather to take the weighted average intensities of different peaks and estimate a single ![]() [763].
[763].
That the stresses associated with the plasticity (Fig. 103) are small is a reflection of the fact that the deformation is due to martensitic transformation of retained austenite rather than ordinary plasticity involving slip dislocations. Indeed, it is found in compression experiments on quenched and tempered 52100 steel that most of the retained austenite present in the initial microstructure decomposes into martensite at strains less than 0.05 [801].
| Transformation | ||
| Martensite | 0.24 | 0.03 |
| Bainite | 0.22 | 0.03 |
| Widmanstätten ferrite | 0.36 | 0.03 |
![\includegraphics[width=0.98\linewidth]{Christ_uniaxial.eps}](img584.png) |
The changes in retained austenite content of the steel as a function of fatigue loading with a stress amplitude of 1500 MPa have also been studied [29], Table 6. Much of the austenite decomposes in the first cycle of fatigue. When the very first part of the cycle begins with compression, the retained austenite content hardly changes, because the stress then acts against any volume change due to transformation. It is also interesting that changes in ![]() following the first cycle are minimal, presumably because of mechanical stabilisation [804, 805, 807, 806, 803, 802, 809, 808, 810] and due to the refinement of the remaining austenite, which has the effect of reducing the
following the first cycle are minimal, presumably because of mechanical stabilisation [804, 805, 807, 806, 803, 802, 809, 808, 810] and due to the refinement of the remaining austenite, which has the effect of reducing the ![]() temperature [814, 815, 812, 811, 813].
temperature [814, 815, 812, 811, 813].
| Number of cycles | ||
| 0 | 11.7 | 11.0 |
| 10 | ||
| 1 | 3.1 | 4.7 |
| 50 | 3.7 | 11.0 |
There is a peculiar effect that the plastic deformation of retained austenite can either make it stable or unstable with respect to martensitic transformation. It is nucleation which limits the formation of martensite [818, 817] so the introduction of deformation-induced defects can accelerate transformation. However, the interface connecting martensite and austenite has a dislocation structure which is glissile; any obstacles placed in its path will hinder the progress of the transformation. A sufficiently large density of defects in the austenite can completely suppress the transformation, a phenomenon known as mechanical stabilisation [804, 802, 803]. The term `sufficiently large', is in the context of the free energy difference driving the ![]() Change; if the magnitude of the latter is large then the onset of mechanical stabilisation occurs at a larger number density of defects [809].
Change; if the magnitude of the latter is large then the onset of mechanical stabilisation occurs at a larger number density of defects [809].
The defects that lead to stabilisation can be induced by the transformation itself; thus, bainite plates stop growing before they impinge hard obstacles because of the plastic collapse of the surrounding austenite [809, 819]. There is one study published on 52100 steel in which the formation of isothermal martensite creates defects which mechanically stabilises the remaining retained austenite to further transformation [820, 194].
Ferrite is ferromagnetic under ambient conditions in low-alloy steels, whereas austenite has rather complicated magnetic properties but on average can be regarded as non-magnetic. This means that the transformation of austenite is accelerated, i.e.,there is a rise in the martensite-start temperature, when it occurs under the influence of an external magnetic field [822, 823, 821]. Equation 40would then suggest that the amount of austenite retained at ambient temperature should decrease. However, there are some odd results reported for 52100 steel where the application of magnetic fields during heating to the austenitisation temperature led to changes in the retained austenite content, Fig. 104. The changes observed, although consistent, are rather small and possibly within the experimental error associated with retained austenite measurements. Other experiments indicated significant improvements in the fatigue properties; this subject needs further investigation.
![\includegraphics[width=0.98\linewidth]{Gheorghies.eps}](img586.png) |
Changes is component dimensions are attributed to a large variety of phenomena, many of which have been described by Mayr [825]. The key aspects covered in various parts of this review are summarised in Fig. 105, and specific issues relating to microstructure discussed in this section.
The dimensional changes that occur as a consequence of alterations in microstructure can be significant when considered, for example, in the context of the tolerances associated with fitting bearings on shafts. The first precipitate to form during the tempering of martensite between 50-150 ![]() C in the 52100 steel is
C in the 52100 steel is ![]() -carbide which causes negligible shrinkage [791], the strains typically being less than
-carbide which causes negligible shrinkage [791], the strains typically being less than ![]() [826]. It is the volume expansion due to the decomposition of retained austenite that dominates dimensional change, with some compensation due to shrinkage if the conditions are appropriate for the precipitation of cementite (Fig. 106). The observed strain is about
[826]. It is the volume expansion due to the decomposition of retained austenite that dominates dimensional change, with some compensation due to shrinkage if the conditions are appropriate for the precipitation of cementite (Fig. 106). The observed strain is about ![]() per percent of retained austenite that decomposes in a 52100 type steel.
per percent of retained austenite that decomposes in a 52100 type steel.
![\includegraphics[width=0.98\linewidth]{Hengerer.eps}](img590.png) |
Given a detailed knowledge of the quantities, chemical compositions and densities of the phases that occur in steels, it is in principle possible to calculate the changes in size that occur when steel is subjected to heat treatment [827, 831, 830, 828, 829]. Similar work has been done in the context of bearing steels, in an attempt to relate observed dimensional changes those due either to phase transformation or due to tempering reactions [220, 832, 833]. The problem is relatively simple when describing isotropic strains due to the transformation of a single phase, for example, the case where retained austenite decomposes into a mixture of cementite and ferrite. The complexity increases dramatically when discussing tempering, which in practice involves many reactions occurring simultaneously, so that somewhat arbitrary assumptions must be made in dividing the decomposition into separable stages. A comparison between calculations and observations then inevitably requires a level of fitting to the experimental data. For example, in the most recent work on 52100 steel [220] it is assumed that carbon is more stable in cementite than at dislocations whereas it is known that the introduction of dislocations causes the dissolution of cementite [834].
The decomposition of retainedaustenite into martensite, either under the influence of stress or when the steel is cooled below ambient temperature, must lead to dimensional changes given that the density of the parent phase is greater than that of the product. The resulting expansion is of the order of 4m per 100 µmm [835]; this of course is a much smaller strain than expected if a fully austenitic 52100 steel were to transform into martensite [836]. Such changes have been measured for bearing steels and although the heat-treatment conditions were not fully reported, the strain increases as the transformation is suppressed to lower temperatures [832]. This is because difference in density increases for transformation at lower temperatures since the thermal expansion coefficient of austenite is much greater than that of ferrite. However, this change has been demonstrated to be much smaller than the distortion that occurs during quenching [23]. Nevertheless, for bearings which are in service, the transformation of austenite can lead to a change in clearance [769], which in turn can alter the state of stress [32]. The transformation product is untempered martensite; this may or may not embrittle the steel depending on the scale of the region of austenite available for transformation [223, 222]. Fine particles of untempered, high-carbon martensite do not crack because of the difficulty in transferring stress over small length scales [236].
The magnitude of the volumetrictransformation strain is illustrated in Fig. 107a, for a carburised steel which initially contains about 35% of retained austenite, when subjected to fatigue by axial loading ( ![]() ), as a function of the test temperature. The volumetric transformation strain decreases as the test temperature is increased primarily because the thermodynamic stability of the austenite increases and it becomes less susceptible to stress-induced martensitic transformation.
), as a function of the test temperature. The volumetric transformation strain decreases as the test temperature is increased primarily because the thermodynamic stability of the austenite increases and it becomes less susceptible to stress-induced martensitic transformation.
|
(a)
![\includegraphics[width=0.40\textwidth]{Neu_strain.eps}](img591.png) (b) (b) ![\includegraphics[width=0.50\textwidth]{Neu_anisotropic.eps}](img592.png)
|
The transformation strains need not be isotropic if there is a bias in the crystallographic variants of martensite or bainite that form [761, 839, 838, 789, 837]. This is because the formation of each plate causes both a shear ( ![]() 0.26) and dilatational strain (
0.26) and dilatational strain ( ![]() 0.03) [100]. Each austenite grain can transform into 24 variants and if all of these form then the shear strain is effectively cancelled on a macroscopic scale in a polycrystalline sample. It is only if an applied stress or other external field favours the formation of particular plates which comply better with the field, that the microstructure becomes biased and the shear strains manifest themselves, leading to anisotropic transformation strains (Fig. 108). Transformation strains which vary with the orientation relative to the stress axis have been reported for a carburised bearing steel initially containing a large quantity of retained austenite [35]. The austenite partly decomposed into martensite during fatigue testing with elongation along the tensile axis and contraction along the other orthogonal axes.
0.03) [100]. Each austenite grain can transform into 24 variants and if all of these form then the shear strain is effectively cancelled on a macroscopic scale in a polycrystalline sample. It is only if an applied stress or other external field favours the formation of particular plates which comply better with the field, that the microstructure becomes biased and the shear strains manifest themselves, leading to anisotropic transformation strains (Fig. 108). Transformation strains which vary with the orientation relative to the stress axis have been reported for a carburised bearing steel initially containing a large quantity of retained austenite [35]. The austenite partly decomposed into martensite during fatigue testing with elongation along the tensile axis and contraction along the other orthogonal axes.
Given the anisotropy in plasticity when phase change occurs under the influence of an external stress, it is not appropriate, as is sometimes done, to represent the transformation plasticity in terms of a single parameter as is sometimes done [840]. The stress particularly favours the development of a non-random structure when the transformation mechanism is displacive (Widmanstätten ferrite, bainite, martensite) and hence the anisotropy. With individual plates of martensite and bainite, both the volume change and shear strain are not isotropic. Thus, a longitudinal strain of about 0.02 was observed when 52100 steel was transformed into martensite whilst exposed to a tensile stress of about 250 MPa [840]. This is large and inconsistent with volume strain on its own; it is a reflection of the fact that the martensite that develops will not be randomly oriented.
Fig. 107b shows illustrates the anisotropic transformation strains when a carburised steel initially containing 35% retained austenite is loaded in tension; the corresponding data when the sample is fatigue loaded are shown as points. It is why the anisotropy is much smaller during fatigue loading, and why ![]() and
and ![]() become almost equal after eight cycles of fatigue loading.
become almost equal after eight cycles of fatigue loading.
The general influence of retained austenite when subjected to fatigue loading at a variety of temperatures is summarised in Fig. 109. The athermal part is simply the transformation strain when the steel is quenched from the austenitisation temperature to ambient. The stress affected transformation is the next stage, with the strain decreasing as thermodynamic stability of the retained austenite increases with test temperature. However, at sufficiently high temperatures, the retained austenite becomes thermally unstable and transforms into bainite, introducing the time-dependent component of strain. It is known that all of the austenite retained in 52100 steel quenched from temperatures in the range 800-850 ![]() C is decomposed by tempering at 260
C is decomposed by tempering at 260 ![]() C or above [182].
C or above [182].
![\includegraphics[width=0.98\linewidth]{shape.eps}](img595.png) |
![\includegraphics[width=0.98\linewidth]{Neu_schematic.eps}](img596.png) |
| < /td> |
Plastic deformation can lead to a decrease in density when accompanied by the creation of defects such as dislocations. However, in a comparison of martensitic and bainitic bearing-steel 100CrMnMo8 (Table: 1), these changes have been shown to be small when compared with those associated with the decomposition of retained austenite [216].
The deviation of the dimensions and shape of a bearing component during the course of manufacture adds considerably to the expense of manufacture, so it is not surprising that the subject is well rehearsed and there exist long lists of factors which influence the distortion [841]. The focus here is on the distortion due to the variation of temperature with position within the component, which may or may not be influenced by phase transformations.
The uneven distribution of mass during heat treatment leads to variations in cooling rate across the component. This can in principle be minimised by adjusting the quenching conditions such that the product of the dimensionless quantities the Fourier number and the Biot number is kept constant over the geometry of the component [842]. A small Fourier number corresponds to a larger amount of heat stored in the work piece, i.e.,a greater mean temperature. The Biot number indicates the relative roles of heat transfer by thermal conduction and across interfaces; it can therefore be altered by varying, for example, the quench medium.
The temperature distribution can also become heterogeneous when dealing with large components of uniform shape when they must be cooled rapidly. Different parts of the sample do not transform at the same instance of time so that the transformation strains are not synchronised as a function of location within the specimen. It follows that anything which reduces the temperature gradients within the sample helps minimise distortion. This is illustrated in Fig. 110which shows experiments in which a cut asymmetric ring is heat treated in different circumstances. The difference in the gap before and after heat-treatment is taken as a measure of distortion [23]. Water quenching leads not only to the highest distortion but also the most erratic behaviour, because of the formation of a vapour blanket and the collapse of the vapour envelope before conduction and convection take over. This is not the case with oil as the quenching medium. The distortion also decreases when the temperature of the quenching medium is reduced.
Martempering involves quenching the component, usually into a salt bath, to a temperature which is just above that at which martensite forms [843]. It is then held at that temperature, for a time period during which the austenite remains untransformed, in order to allow the thermal gradients to homogenise, followed by air cooling through the martensite transformation temperature range. Martempering is associated with the smallest distortion of all the methods illustrated in Fig. 110.
|
(a)
![\includegraphics[width=0.25\textwidth]{Distortion_ring.eps}](img597.png) (b) (b) ![\includegraphics[width=0.55\textwidth]{distortion_Adachi.eps}](img598.png)
|
Stresses which exist over long distances cannot readily be relieved without heat treatment that promotes long-range atomic diffusion. It is surprising therefore, that experiments conducted on split rings made from 52100 steel, which are elastically stressed by inserting wedges into the split [844], indicate that there are substantial changes during tempering even at low temperatures, Fig. 111. Dislocation rearrangements and carbon migration are feasible even at room temperature, and lead to an increase in the yield strength by making the material more mechanically homogeneous [845]. However, these are probably insufficient to cause substantial changes in imposed stress, which is said to be related to structural changes within the material, although direct evidence is lacking. The extent of relief increases with the carbon concentration of the martensite; it is postulated that the volume changes associated with carbide precipitation cause plasticity and hence stress relief [846] 19 . There may be a role of other transformation strains - for example, a significant shear strain component which acts to relieve applied stresses by favouring precipitation of those crystallographic variants of carbide which accommodate the stress [847].
![\includegraphics[width=0.98\linewidth]{Brown_1962.eps}](img599.png) |
When bearings are subjected to heavy loads, plasticity occurs at the contact surfaces causing the formation of shallow grooves which can develop into significant damage [848]. This phenomenon is often studied by assessing the ability of the steel to withstand static contact loads. The presence of austenite can exasperate the effect if it leads to a reduction in the yield strength. This is illustrated for steel 52100 steel in Fig. 112, where it is seen that the softening caused by the presence of austenite leads to deeper grooves. The 0% ![]() Curve shows that the main factor controlling the depth of grooves is the macroscopic hardness, rather than the detailed microstructure. One aspect which is not clear is whether it helps when the austenite undergoes a stress or strain assisted transformation into hard martensite.
Curve shows that the main factor controlling the depth of grooves is the macroscopic hardness, rather than the detailed microstructure. One aspect which is not clear is whether it helps when the austenite undergoes a stress or strain assisted transformation into hard martensite.
![\includegraphics[width=0.98\linewidth]{Drutowski.eps}](img600.png) |
In the majority of applications, the wear of bearing races is not a life-limiting factor given good lubrication and adequate surface finishing [850]. It is when the lubrication fails or when particles are introduced by contamination or detachment from the bearing that wear becomes an issue. The wear process is exaggerated at first while the components `run-in' but then reaches a steady state in which the roughness of the surface remains constant when measured using fractal dimensions [851].There are four main categories of wear debris [852]. Sliding between the contact surfaces can lead to the detachment of flakes typically 15m in length and 1m in thickness. There is an effect known as `peeling' which leads to such flakes and initiates at minor surface defects [7], stimulated by partial metal-to-metal contact for ![]() lubricant conditions. Small spheres (
lubricant conditions. Small spheres ( ![]() m diameter) which are iron-rich but could be compounds of iron form but their origin is not clear [853]. There may be debris from the non-ferrous components of the bearing, such as the retaining cages. Finally, large ferrous particles (
m diameter) which are iron-rich but could be compounds of iron form but their origin is not clear [853]. There may be debris from the non-ferrous components of the bearing, such as the retaining cages. Finally, large ferrous particles ( ![]() m) resulting from spall or even debris contamination from ancillary equipment.
m) resulting from spall or even debris contamination from ancillary equipment.
Wear debris creates the indentations that exacerbate fatigue damage; its detrimental influence can be mitigated by enhancing the fatigue resistance of the bearing steel, but also by allowing some plasticity at the surfaces of the rolling elements in order to accommodate the debris without causing sharp stress concentrations. A greater toughness mitigates the influence of debris-induced damage [854]. Retained austenite is found to be beneficial in this respect [855]. The austenite is more amenable to initial deformation and work done by the debris can cause it to undergo stress or strain-induced transformation into hard martensite, thus enhancing the resistance of the material to further damage [118, 391]. For this reason, the presence of retained austenite gives better rolling contact performance when tested using debris contaminated lubrication [857, 856]. Fig. 113illustrates artificial indents into hardened 52100 steel, as a function of the retained austenite content. The one with the smaller amount of retained austenite results in sharper and somewhat larger upheavals (`lips') surrounding the indent. This may cause the local penetration of the lubricant film and enhanced contact with the rolling elements, whose passage would lead to large stress pulses below the upheavals and hence enhanced spalling. The lip profile is smoother when the steel has a larger quantity of retained austenite, and height of the lip has been shown to decrease systematically as the austenite content is reduced [160].
Early controlled-experiments on the indentation resistance of 52100 steel [816] are consistent with these observations. Large localised strains capable of inducing the austenite to transform into hard martensite led to an improvement in indentation resistance. On the other hand, the material became more sensitive to retained austenite content at small indentation strains because the austenite is a softer constituent when compared with the surrounding tempered martensite. An interesting observation which follows from this, is that the indentation resistance improved when the austenite was stronger because the heat-treatment induced an increase its carbon concentration [816].
One difficulty in exploiting retained austenite to make the steel more resistant to indentation is that its transformation causes dimensional changes which may not be tolerable if they are large enough to reduce the efficacy of an interference fit of the bearing to a shaft. Although an effort has been made to discuss the quantity and stability of retained austenite which would lead to better indentation resistance whilst at the same time avoiding compromising fit [858], there is no quantitative understanding in this area. The suggestion that ![]() should be greater than 0.05 to enhance indentation resistance, and that the stability of the austenite in 52100 steel is too low to be exploited in this respect, must at this stage be regarded as unproven. After all, there have been many studies described above which do demonstrate an enhancement of 52100 by retained austenite in the presence of debris damage.
should be greater than 0.05 to enhance indentation resistance, and that the stability of the austenite in 52100 steel is too low to be exploited in this respect, must at this stage be regarded as unproven. After all, there have been many studies described above which do demonstrate an enhancement of 52100 by retained austenite in the presence of debris damage.
Steels in the 52100 category are partially austenitised and after quenching achieve a microstructure which is a mixture of undissolved cementite, untempered martensite and a small amount of retained austenite. The martensite is then tempered in the range 160 -250 ![]() C. The martensite plates are fine, approximately 0.2m in thickness and although they contain dislocations, electron diffraction patterns from the plates are reasonably sharp and distinct, Fig. 114. This initial microstructure changes when subjected to contact fatigue, with dramatic alterations detectable in the zone subjected to the largest shear stresses. The changes have conventionally been observed using optical microscopy and hence a terminology has evolved, based on the contrast that develops relative to the unaffected steel when the sample is etched with nital; picric acid based etchants are not effective in revealing this form of damage [859]. The so-called dark-etching regions evolve first and www.phase-trans.msm.cam.ac.uk-etching bands develop within these darker areas.
C. The martensite plates are fine, approximately 0.2m in thickness and although they contain dislocations, electron diffraction patterns from the plates are reasonably sharp and distinct, Fig. 114. This initial microstructure changes when subjected to contact fatigue, with dramatic alterations detectable in the zone subjected to the largest shear stresses. The changes have conventionally been observed using optical microscopy and hence a terminology has evolved, based on the contrast that develops relative to the unaffected steel when the sample is etched with nital; picric acid based etchants are not effective in revealing this form of damage [859]. The so-called dark-etching regions evolve first and www.phase-trans.msm.cam.ac.uk-etching bands develop within these darker areas.
|
(a)
![\includegraphics[width=0.7\textwidth]{Mitamura_before.eps}](img604.png) (b) ![\includegraphics[width=0.7\textwidth]{Mitamura_before_dark.eps}](img605.png)
|
In high quality 52100 type steels, rolling contact loading causes a subsurface region approximately 0.3mm in depth to appear relatively dark when an etched sample is observed in an optical microscope; i.e.,relative to the unaffected steel [860, 705]. The effect is observed typically after a few million cycles of contact. The region is dark relative to the virgin microstructure which remains at greater depths; its upper boundary is well-defined whereas the lower regions are diffuse, Fig. 115a,b. The contrast arises because the structure is heterogeneous on a fine scale, consisting of severely deformed bands separated by largely unaffected tempered martensite [741, 705, 859]. The nital etchant preferentially attacks the deformation bands leaving deep grooves which on the scale of optical microscopy result in the dark contrast.
The depth at which the dark-etching area is created varies according to the loading conditions [861] but is generally centred around the position of maximum shear stress [741, 8]. Electron diffraction patterns from this zone reveal a greater spread in orientations, and transmission electron micrographs show that the original plates of martensite are deformed, and that each plate now contains significant misorientations almost in the form of cell structures [862, 863]. This is consistent with the observed change in the electron diffraction pattern. The large cementite particles present due to incomplete austenitisation are not significantly affected at this stage in damage evolution, but the fine carbide particles introduced during low-temperature tempering apparently dissolve in the process of cyclic deformation [862] but the carbon must re-precipitate elsewhere since the region is observed to soften relative to the virgin material. This reprecipitation is thought from electron microscopy observations to be that of ![]() -carbide [864]. The tendency to etch dark is a consequence of the deep groves produced from `carbide discs' sandwiched between the ferrite-like phase [741], together with the heterogeneous deformation of the initial structure Fig. 116.
-carbide [864]. The tendency to etch dark is a consequence of the deep groves produced from `carbide discs' sandwiched between the ferrite-like phase [741], together with the heterogeneous deformation of the initial structure Fig. 116.
|
(a)
![\includegraphics[width=0.55\textwidth]{Lund_dark.eps}](img606.png) (b) (b) ![\includegraphics[width=0.35\textwidth]{dark_groove.eps}](img607.png) (c) ![\includegraphics[width=0.45\textwidth]{Osterlund_2a.eps}](img608.png) (d) (d) ![\includegraphics[width=0.45\textwidth]{Osterlund_8e.eps}](img609.png)
|
The dark-etching region is sometimes said to be an over-tempered form of the virgin microstructure and is somewhat softer at 53 HRC compared with the 61 HRC before rolling contact [865, 705, 862]. There may or may not be adiabatic heating associated with localised plastic deformation. The meaning or mechanism of tempering is not clear in the literature on bearing steels, given that the damage arises during rolling contact. There is talk of dynamic creep induced by fatigue loading, accompanied by carbon migration and microscopic stress relief [866]. However, it is in general possible to rearrange dislocations into cell structures under the influence of cyclic deformation. Cyclic softeningin quenched and tempered martensitic steels occurs when these rearrangements of the dislocation substructure lead to a reduction in dislocation density [867]. There is in effect a mechanical removal of excess dislocations. The fact that dislocations may become unpinned, for example from atmospheres of carbon, also leads to softening [868]; this kind of softening is akin to the Bauschinger effect since some of the plastic strain then becomes reversible [100]. It would be worth verifying these interpretations by generating cyclic stress-strain curves.
The interpretation that the dark-etching region is an effectively an over-tempered region of martensite, is consistent with the observation that this region is not observed if the steel is first tempered to a hardness of 57 HRC; only the www.phase-trans.msm.cam.ac.uk bands described in section 21.2appear during fatigue [869].
|
(a)
![\includegraphics[width=0.7\textwidth]{Mitamura_after1.eps}](img610.png) (b) ![\includegraphics[width=0.7\textwidth]{Mitamura_after2.eps}](img611.png)
|
These areas develop within the dark-etching region when the latter is subjected to prolonged rolling contact. They are in the form of short, irregular layers in three dimensions [870]. They have two striking characteristics: (a) they reveal no internal contrast using optical microscopy and hence etch www.phase-trans.msm.cam.ac.uk or light grey, (b) they have characteristic directionality, Fig. 117. The lack of contrast in this case is because the scale of the structure is much finer than the resolution of an optical microscope. There are actually two kinds of bands, the high-angle bands (HABs) which are steeply inclined to the contact surface, and less striking low-angle bands (LABs). The bands develop deep within the steel and propagate towards the surface. The HAB's generally appear after the bearing has experienced very long service, or following rolling tests in which the contact stress is greatly exaggerated.
![\includegraphics[width=0.65\textwidth]{Lund_light.eps}](img612.png) |
The propagation of the bands occurs across features such as prior austenite grain boundaries (in Fig. 115d), the bands are longer than the typically 50 ![]() m sized austenite grains), and their development does not necessarily parallel the strengthening of specific crystallographic textures that form due to rolling contact deformation [871].
m sized austenite grains), and their development does not necessarily parallel the strengthening of specific crystallographic textures that form due to rolling contact deformation [871].
Higher resolution observations have suggested that these layers are subjected to traumatic levels of localised deformation, which is so intense that dynamic recrystallisation occurs and leaves a fine equiaxed structure of grains which have a size of the order of 20nm [30, 863], Fig. 118. The electron diffraction pattern shows rings corresponding to myriads of orientations of fine grains. There can be further structure within the layers; there may be amorphous regions, again indicative of severe deformation, and extremely small voids. The interface between the amorphous and crystalline regions is not strong and has been shown to crack [30].
The notion that a steel recrystallises locally during rolling contact at near ambient-temperatures (55-90 ![]() C) is at first sight implausible; localised plasticity can produce adiabatic heating and temperatures in excess of 700
C) is at first sight implausible; localised plasticity can produce adiabatic heating and temperatures in excess of 700 ![]() C have been speculated but are not yet supported by evidence [872]. The driving force for recrystallisation should be large if the www.phase-trans.msm.cam.ac.uk bands are generated by intense localised deformation, and the resulting defects may also assist the processes of diffusion. Crystallographic determinations suggest that a
C have been speculated but are not yet supported by evidence [872]. The driving force for recrystallisation should be large if the www.phase-trans.msm.cam.ac.uk bands are generated by intense localised deformation, and the resulting defects may also assist the processes of diffusion. Crystallographic determinations suggest that a ![]() sub-surface texture develops in the damaged material with large rolling contact stresses (3.8GPa) and at temperatures in excess of 55
sub-surface texture develops in the damaged material with large rolling contact stresses (3.8GPa) and at temperatures in excess of 55 ![]() C, consistent with the recrystallisation texture observed when cold-rolled ferritic steels are annealed [871] 20 . In contrast, a
C, consistent with the recrystallisation texture observed when cold-rolled ferritic steels are annealed [871] 20 . In contrast, a ![]() texture is found at relatively low contact stresses and temperatures, which is consistent with the deformation texture of cold-rolled ferritic steels. X-ray line broadening measurements for the two cases are consistent with the recrystallised and deformed states respectively.
texture is found at relatively low contact stresses and temperatures, which is consistent with the deformation texture of cold-rolled ferritic steels. X-ray line broadening measurements for the two cases are consistent with the recrystallised and deformed states respectively.
The evidence suggests that these bands are softer than either the unaffected steel or the dark-etching regions. This might be explained by the observation that they are depleted in carbon; Beswick has measured the concentration in the high-angle bands of damaged 52100 steel to be as low as 0.06 wt%, with an enrichment of the surrounding region to some 1.3 wt% [873]; there is some indirect confirmatory evidence based on autoradiography [874]. Recrystallisation involves diffusion so it is in principle feasible that carbon would partition into the adjacent dark-etching areas to become trapped at dislocations, or to precipitate as layers of cementite [875]. An alternative mechanism is that in the locally plasticised www.phase-trans.msm.cam.ac.uk-region, dislocations break away from their carbon atmospheres, leaving a supersaturation of carbon in the ferrite, which then partitions into the surrounding region to precipitate as cementite [8, 876]. Early suggestions indicated that the cementite would be in the form of layers between the www.phase-trans.msm.cam.ac.uk-etching band and darker matrix [870, 875] but transmission electron microscopy has indicated that in some cases the cementite may precipitate as fine particles [876]. Fig. 119shows that the hardness goes through a minimum in the regions where the www.phase-trans.msm.cam.ac.uk bands develop [877] and the reduction in hardness can be as large as 9 HRC [314]. Softening of this kind, nor the development of bands, occurs when the secondary hardening M50 or M50 NiL are subjected to similar loading. The sources and sinks for the carbon in 52100 steel are cementite particles, which are far less stable than the alloy carbides of the secondary hardening steels [314].
Recent work based on electron probe microanalysis and atomic emission spectroscopy has confirmed the redistribution of carbon from the www.phase-trans.msm.cam.ac.uk bands to the adjacent region (where it precipitates) [879, 878]. Microhardness tests proved the bands to be softer than the material unaffected by rolling contact, but the overall hardness was still high at 600HV, possibly because of the unusually large contact stresses used of 6GPa, in which case the softened regions could be subsequently deformed.
There has been a suggestion that the www.phase-trans.msm.cam.ac.uk bands are a consequence of adiabatic shear [880]; such effects arise when a material has an especial tendency to weaken with increasing temperature during high strain-rate deformation; typical strain rates associated with shear localisation in steels are said to be in excess of ![]() []. Any deformation that is initiated locally then causes the temperature there to increase relative to the surroundings, leading to further weakening and localisation of deformation. The strain rate during such phenomena must be large enough to avoid the dissipation of this heat. Such a mechanism would of course be consistent with the softening that is observed. In HY100 martensitic structural steel used in the manufacture of naval ships, the temperature increase associated with the shear bands has been estimated to be of the order of 600
[]. Any deformation that is initiated locally then causes the temperature there to increase relative to the surroundings, leading to further weakening and localisation of deformation. The strain rate during such phenomena must be large enough to avoid the dissipation of this heat. Such a mechanism would of course be consistent with the softening that is observed. In HY100 martensitic structural steel used in the manufacture of naval ships, the temperature increase associated with the shear bands has been estimated to be of the order of 600 ![]() C [881, 882]. In other work on the same steel, the hardness distribution within the adiabatic shear bands has been found not be uniform, depending on the level of recovery [883]. It is notable that adiabatic shear bands have long been known to etch www.phase-trans.msm.cam.ac.uk [209].
C [881, 882]. In other work on the same steel, the hardness distribution within the adiabatic shear bands has been found not be uniform, depending on the level of recovery [883]. It is notable that adiabatic shear bands have long been known to etch www.phase-trans.msm.cam.ac.uk [209].
One puzzle is that the relative softness of the www.phase-trans.msm.cam.ac.uk bands is in contrast to other White matter, viz. the butterflies and continuous www.phase-trans.msm.cam.ac.uk layers that form on surfaces subjected to both fatigue and sliding, where the White matter is found to be harder than the original steel at about 75 HRC [865, 127]. And furthermore, there is clear evidence that the passage of a band across a cementite particle causes the latter to dissolve [19] (Fig. 120); the argument is that in the case of the bands, the carbon migrates out of the band and precipitates as cementite. One piece of evidence which may resolve the puzzle is that the bands are not associated with cracks; butterflies on the other hand, inevitably nucleate from features which are disconnections, i.e.,cracks in the form of disbonded interfaces, free surfaces at voids and microcracks. It is then the repeated impact of the cracked faces against each other that leads to the severe deformation and associated processes that causes intense hardening and observed structural refinement. Indeed, it has long been postulated that microcracks of one form or another precede White matter [884]. In a rather elegant recent experiment in which powder metallurgy was used to produce a sample of 52100 steel containing voids, rolling contact fatigue cracks initiated at the pores were shown conclusively to precede the formation of White matter, and the severe deformation associated with this matter was verified using crystallographic imaging [885]. This would also explain the different roles of carbon, with this interstitial being rejected from the bands, but dissolved due to severe deformation in the butterfly. The mechanism of dissolution in the latter case is simple, that the chemical potential of carbon at defects is lower than when it is present in cementite [78, 886, 834].
|
(a)
![\includegraphics[width=0.7\textwidth]{Mitamura_after3.eps}](img616.png) (b) ![\includegraphics[width=0.7\textwidth]{Mitamura_after4.eps}](img617.png)
|
![\includegraphics[width=0.98\linewidth]{Steindorf_1987.eps}](img618.png) |
|
(a)
![\includegraphics[width=0.45\textwidth]{Swahn_1.eps}](img619.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Swahn_2.eps}](img620.png)
|
Observations in a 1C-1.5Cr-0.5Mo steel (Table 1) subjected to lubricated rolling contact at 4.2GPa with a slip ratio of 14% have demonstrated sub-surface www.phase-trans.msm.cam.ac.uk layer formation without the influence of hydrogen. Rolling contact in association with sliding gives more intense shear stresses within the material as compared with rolling contact alone. The layers in two-dimensional sections were found to be inclined at angles averaging 30 ![]() (LAB) and 160
(LAB) and 160 ![]() (HAB) to the direction in which the roller moves, Fig. 122. The orientation of banding can be changed by reversing the direction of the rolling contact [871]; the orientation therefore is a function of the deformation history.
(HAB) to the direction in which the roller moves, Fig. 122. The orientation of banding can be changed by reversing the direction of the rolling contact [871]; the orientation therefore is a function of the deformation history.
Finite element simulations have revealed a strong correlation between the angular orientation of concentrated plastic activity and that of experimentally observed www.phase-trans.msm.cam.ac.uk bands in rolling contact fatigue, Fig. 121. The physical mechanism for the development of the two orientations is related to the fact that the principal axes of the stress and strain rotate as the rolling element translates over the substrate; the equivalent strain increments are maximum at the particular orientations associated with the www.phase-trans.msm.cam.ac.uk bands. The same models, however, indicate equal plastic activity in conjugate orientations ( i.e. ![]() and
and ![]() ) [887]. This is inconsistent with observations in which only one set of orientations is seen, but the discrepancy may be accounted by the failure to consider the deformation history.
) [887]. This is inconsistent with observations in which only one set of orientations is seen, but the discrepancy may be accounted by the failure to consider the deformation history.
![\includegraphics[width=0.98\linewidth]{shear_strain.eps}](img623.png) |
Whereas the structure of the www.phase-trans.msm.cam.ac.uk bands is fairly well understood, it is not clear why deformation localises, and often results in patterns of layers. Whereas nucleation on defects or foreign particles can explain their distribution, the fact that the plasticity is confined to layers implies processes which lead to local softening, and frankly, there seems to be little understanding of the processes leading to softening.
![\includegraphics[width=0.98\linewidth]{angle_Harada.eps}](img624.png) |
In general, the formation of www.phase-trans.msm.cam.ac.uk regions is suppressed in the dark-etching areas, possibly because the formation of the latter acts to homogenise stresses. However, the two types of structures can overlap if the www.phase-trans.msm.cam.ac.uk areas are induced first, to be engulfed later by the gradually developing dark-etching regions [862].
www.phase-trans.msm.cam.ac.uk-etching surface layers are common on railway tracks where rolling-contact and sliding damage occurs, on machined surfaces and in general where steel surfaces rub together [888]. The discussion on this has focussed on whether the interaction between the wheel and rail leads to temperatures sufficiently high to austenitise the steel, in which case the www.phase-trans.msm.cam.ac.uk layer might consist of severely deformed martensite; the alternative is that the initial microstructure is mechanically alloyed to produce carbon supersaturated ferrite. 21 The www.phase-trans.msm.cam.ac.uk character comes from the fine scale of the structure which is homogeneous relative to the virgin material.
Early transmission electron microscopy and transient temperature estimates suggested that the www.phase-trans.msm.cam.ac.uk layer is simply severely deformed ferrite in which cementite is dissolved by mechanical alloying [889]. More recent finite element modelling disputes the temperature calculations, and in combination with atom-probe analytical information, suggests that the layers consist of fine martensite [890].
The so-called hard turningprocess involves the machining of hardened bearing steel as an alternative to grinding operations. Machining operations like these, with cutting tools which are worn, also lead to high cutting temperatures and hence to www.phase-trans.msm.cam.ac.uk layers which have been proven to be the result of austenitisation followed by partial transformation into martensite (the residue being retained austenite) [891, 892]. It has long been recognised that the retained austenite content of the surface can be increased by heavy grinding operations [893] or indeed, turning [894]. It is estimated that local temperatures in the range 1190-1250 ![]() C are reached although the details must depend on the specific process. These high temperatures are to be compared against admittedly crude estimates of 550-650
C are reached although the details must depend on the specific process. These high temperatures are to be compared against admittedly crude estimates of 550-650 ![]() C of the temperature at which austenite formation can begin in 52100 steel subjected to equivalent stresses of 1300 MPa and large plastic strains during machining [895, 896]. Under equilibrium conditions and at ambient pressure, the lowest temperature at which austenite appears in this alloy is 720
C of the temperature at which austenite formation can begin in 52100 steel subjected to equivalent stresses of 1300 MPa and large plastic strains during machining [895, 896]. Under equilibrium conditions and at ambient pressure, the lowest temperature at which austenite appears in this alloy is 720 ![]() C (Fig. 4). Reducing the cutting speed helps keep the temperatures low and hence avoids www.phase-trans.msm.cam.ac.uk-layer formation [897], but obviously compromises productivity. A processing map illustrating the domains of different combinations of thermal and severe plasticity contribute to www.phase-trans.msm.cam.ac.uk layer formation is illustrated in Fig. 123.
C (Fig. 4). Reducing the cutting speed helps keep the temperatures low and hence avoids www.phase-trans.msm.cam.ac.uk-layer formation [897], but obviously compromises productivity. A processing map illustrating the domains of different combinations of thermal and severe plasticity contribute to www.phase-trans.msm.cam.ac.uk layer formation is illustrated in Fig. 123.
![\includegraphics[width=0.98\linewidth]{Umbrello_2010.eps}](img625.png) |
Steels like 52100 steel are more susceptible to www.phase-trans.msm.cam.ac.uk layer formation when compared with say M50, because of its greater austenitisation temperature (1100 ![]() C) compared with 840
C) compared with 840 ![]() C for the 52100 steel [714, 168]. Fig. 124shows the www.phase-trans.msm.cam.ac.uk layer thickness as a function of tool flank-wear, for 52100 steel (57 HRC) machined using a polycrystalline cubic boron-nitride tool 22 , for a variety of cutting speeds and feed rates [899]. The results show that the www.phase-trans.msm.cam.ac.uk layer thickness varies dramatically with the material removal rate but is insensitive to the degree of tool wear. This contradicts work which concludes that flank wear is a key feature determining www.phase-trans.msm.cam.ac.uk layer generation [900].
C for the 52100 steel [714, 168]. Fig. 124shows the www.phase-trans.msm.cam.ac.uk layer thickness as a function of tool flank-wear, for 52100 steel (57 HRC) machined using a polycrystalline cubic boron-nitride tool 22 , for a variety of cutting speeds and feed rates [899]. The results show that the www.phase-trans.msm.cam.ac.uk layer thickness varies dramatically with the material removal rate but is insensitive to the degree of tool wear. This contradicts work which concludes that flank wear is a key feature determining www.phase-trans.msm.cam.ac.uk layer generation [900].
www.phase-trans.msm.cam.ac.uk layers produced during the machining of 52100 steel are harder than the substrate tempered martensite, and hence increase the resistance to sliding wear; however, there is a need for further work on the influence of hard turning on fatigue life [897].
![\includegraphics[width=0.98\linewidth]{Cappellini.eps}](img626.png) |
The grinding of hardened bearing steels of the 52100 steel class leaves a www.phase-trans.msm.cam.ac.uk layer at the surface with a hardness in excess of 900HV and in a state of tension ( ![]() MPa) with penetrating microscopic cracks in regions where the layers are relatively thick [902]. Fig. 125shows a more comprehensive study of stress distributions in which hard turned or ground surfaces of 52100 steel (815
MPa) with penetrating microscopic cracks in regions where the layers are relatively thick [902]. Fig. 125shows a more comprehensive study of stress distributions in which hard turned or ground surfaces of 52100 steel (815 ![]() C for 2h, quenched into oil at 65
C for 2h, quenched into oil at 65 ![]() C for 15min, tempered 176
C for 15min, tempered 176 ![]() C for 2h, 61-62 HRC [903]). www.phase-trans.msm.cam.ac.uk layer formation was induced during turning by using a worn tool, and in the case of grinding by removing the lubricant. The undulations in the curves are likely to be a reflection of the accuracy of the stress measurements rather than real fluctuations, but it can reasonably be concluded that the turning and grinding operations leave the surfaces in a state of compression, whereas the same processes, when they lead to www.phase-trans.msm.cam.ac.uk layer formation, leave tensile residual stresses. As a result, the rolling contact fatigue life, measured at the large Hertzian stress of 4629 MPa, decreases dramatically in the presence of the www.phase-trans.msm.cam.ac.uk layers. The claimed influence on rolling contact fatigue is surprising given that the detrimental layers and stresses have limited depth when compared with the sub-surface region with the largest shear stresses. This contradiction may have its origin in the way in which the fatigue life was defined [892], with failure corresponding to the observation of shallow damage, penetrating some 20 µm.
C for 2h, 61-62 HRC [903]). www.phase-trans.msm.cam.ac.uk layer formation was induced during turning by using a worn tool, and in the case of grinding by removing the lubricant. The undulations in the curves are likely to be a reflection of the accuracy of the stress measurements rather than real fluctuations, but it can reasonably be concluded that the turning and grinding operations leave the surfaces in a state of compression, whereas the same processes, when they lead to www.phase-trans.msm.cam.ac.uk layer formation, leave tensile residual stresses. As a result, the rolling contact fatigue life, measured at the large Hertzian stress of 4629 MPa, decreases dramatically in the presence of the www.phase-trans.msm.cam.ac.uk layers. The claimed influence on rolling contact fatigue is surprising given that the detrimental layers and stresses have limited depth when compared with the sub-surface region with the largest shear stresses. This contradiction may have its origin in the way in which the fatigue life was defined [892], with failure corresponding to the observation of shallow damage, penetrating some 20 µm.
![\includegraphics[width=0.98\linewidth]{Guo_2010.eps}](img628.png) |
| < /td> |
It should be noted that amorphous layers and localised melting have been induced on the surface of 52100 steel [904] but by processes involving the severe rubbing of tungsten carbide against the bearing steel; such experiments do not represent the conditions encountered in service.
There have been several finite element models for estimating www.phase-trans.msm.cam.ac.uk layer formation on the basis of austenitisation through deformation induced heat, followed by rapid quenching. These have been reviewed by Umbrello et al.[217], who incorporated empirical principles in order to model both the www.phase-trans.msm.cam.ac.uk and underlying heat-affected dark regions. An interesting conclusion from this work was that www.phase-trans.msm.cam.ac.uk layer thickness in general increases with the cutting speed but that of the tempered dark layer decreases. The former is because a higher peak temperature is reached, but the mechanism for the reduction in the heat-affected zone which causes the dark region is not clear.
The so-called butterfly wings (Fig. 126) initiate at voids, non-metallic inclusions, carbides or microcracks in steel subjected to rolling contact fatigue [374]. Voids are more susceptible to butterfly formation, followed by debonded or cracked inclusions. Tightly fitting particles have the least susceptibility because the deformation in the steel at the interface between the inclusion and the matrix becomes constrained. For the same reason, voids offer the least constraint to the development of fatigue damage. Fig. 127illustrates that manganese sulphide particles encapsulated in oxides are the most common butterfly initiation sites in modern steels. It is odd that Ti(C,N) particles do not seem to participate in damage initiation during rolling contact experiments but are found to nucleate failure in fatigue tests where the loading is axial (Fig. 79). This may reflect a stronger interface that the titanium carbonitrides have with the steel. The number density of such particles is small and hence a push-pull test, which exposes a large volume to uniform stress, is more likely to discover the Ti(C,N) particles. The microcracks which initiate butterflies are present either in the form of localised fracture at local prior austenite grain boundaries, or within high-carbon martensite plates that form in carburised surfaces of bearings [90].
It has been argued that the formation of the White matter associated with butterflies can occur independently of cracks if the strain amplitude due to cyclic loading is below a certain value; cracking precedes White matter if this value is exceeded [212]. However, this model does not explain localisation, i.e.,why hard White matter should form in a specific region of the steel without some form of decohesion.
|
(a)
![\includegraphics[width=0.85\textwidth]{serial_Becker_1981.eps}](img629.png) (b) ![\includegraphics[width=0.45\textwidth]{serial_2_Becker_1981.eps}](img630.png)
|
![\includegraphics[width=0.98\linewidth]{Lund_2010_inclusions.eps}](img631.png) |
With the contact stresses are low and at levels consistent with service, the damage is perceptible at about 5-10% of the expected ![]() lifetime, with minute cracks at inclusion/matrix interfaces [905]; some have suggested that butterflies can be observed at
lifetime, with minute cracks at inclusion/matrix interfaces [905]; some have suggested that butterflies can be observed at ![]() when the contact stress exceeds 3GPa [118], Fig. 128. It is worth emphasising therefore, that the presence of butterflies does not in itself reflect the onset of traumatic failure, or even of spalling, and this has been recognised for a long time [612, 864]; the limited and loose correlation reported between the number density of butterflies and fatigue life is based on unrealistically high contact stress experiments [143]. Localised plastic deformation of this kind, rarely is associated with fatigue cracks proceeding beyond the close proximity of the altered region. It has been concluded therefore that the reversed plastic deformation that leads to White matter is not an essential step in the creation of inclusion-initiated fatigue cracks [906, 613]. It could be surmised, however, that crack initiation in the process that leads to final failure occurs early during rolling contact fatigue, but the life is determined by how such cracks grow to a point where they make their presence felt in the operation of the bearing. Similar comments apply to the www.phase-trans.msm.cam.ac.uk bands described previously (section 21.2.1); unfailed bearings can contain a high density of the bands within their stressed volumes [612].
when the contact stress exceeds 3GPa [118], Fig. 128. It is worth emphasising therefore, that the presence of butterflies does not in itself reflect the onset of traumatic failure, or even of spalling, and this has been recognised for a long time [612, 864]; the limited and loose correlation reported between the number density of butterflies and fatigue life is based on unrealistically high contact stress experiments [143]. Localised plastic deformation of this kind, rarely is associated with fatigue cracks proceeding beyond the close proximity of the altered region. It has been concluded therefore that the reversed plastic deformation that leads to White matter is not an essential step in the creation of inclusion-initiated fatigue cracks [906, 613]. It could be surmised, however, that crack initiation in the process that leads to final failure occurs early during rolling contact fatigue, but the life is determined by how such cracks grow to a point where they make their presence felt in the operation of the bearing. Similar comments apply to the www.phase-trans.msm.cam.ac.uk bands described previously (section 21.2.1); unfailed bearings can contain a high density of the bands within their stressed volumes [612].
![\includegraphics[width=0.98\linewidth]{butterflies_timing.eps}](img633.png) |
In exhaustive experiments, Lund [127] found that the occurrence of butterflies is dependent on the shear stress generated by rolling contact, to exceed 400 MPa in 52100 type steel, Fig. 129. As a result, the depth at which butterflies are observed diminishes as the rolling contact pressure decreases. Furthermore, the trend did not depend on whether the structure of the steel is martensitic or bainitic.
![\includegraphics[width=0.98\linewidth]{Lund_2010_depth.eps}](img634.png) |
The butterfly wings develop into their recognisable form at the late stages of fatigue life, perhaps after tens of millions of contact cycles under service conditions; they therefore can determine the long-term life of a bearing. They may of course develop more rapidly in laboratory tests where the contact stresses or hydrogen contents are often exaggerated.
Although early work associated the phenomenon with phase transformation [50] or even localised melting [908, 907], it is now accepted that the wings represent regions of intense deformation. It is important to realise that the whole process begins with the initiation of a microcrack [658], which then develops into the White matter in a process which involves the rubbing together and intense mechanical deformation at the fractured surfaces. The conclusion follows that butterfly formation can be reduced by any mechanism which enhances the resistance to cracking [658].
The hardness within the wing can exceed 1000-1300 HV, which compares against the 800 HV of a typical bearing steel [90, 50, 910, 909]. 23 . The intensity of deformation leads to the development of a structure whose scale ranges from minute grains tens of nanometers in size, to cracks covering the length of the butterfly wings, as illustrated schematically in Fig. 131. Several high-resolution observations [90, 910] confirm early work using electron diffraction and transmission microscopy, where it was reported that the region within the wings is divided into minute grains (5-50nm in size), in random orientations [50]. The fine grains are puzzling in that they have replaced tempered martensite; most investigators assume from their general morphology that the grains are a result of recrystallisation, whether dynamic or static. Such a change must occur at temperatures not far from ambient, so it is expected that the kinetics of recrystallisation must be slow, unless the defect density created in the www.phase-trans.msm.cam.ac.uk-etching areas is sufficient to provide adequate diffusion to permit recrystallisation. Some authors dismiss dynamic recrystallisation because the time period during which deformation occurs is extremely small in each cycle of rolling contact fatigue. The fact that the grains are finer at the tips of the butterflies than at the origin, might imply some kind of grain growth, although this observation [910] has not yet been discussed in the literature.
The shear stresses inherent in rolling contact act at 45 ![]() to the over-rolling direction in a circumferential section, and can break the interface between the inclusion and steel, assuming the inclusion is not already debonded. It is strange that the wings form along only one of the 45
to the over-rolling direction in a circumferential section, and can break the interface between the inclusion and steel, assuming the inclusion is not already debonded. It is strange that the wings form along only one of the 45 ![]() orientations (inset, Fig. 131); on the basis of the shear stresses, two pairs of differently oriented wings are expected. The clue lies in the fact that the wings are always orientated in the direction of ball motion. It is only when a rolling contact fatigue test is interrupted and the direction of rotation reversed, that four-winged butterflies appear as shown in Fig. 130[913]. This suggests a role of deformation history, i.e., the direction of rolling contact; supporting evidence for this conclusion is that the orientation of the www.phase-trans.msm.cam.ac.uk-etching bands (HABs) can appropriately be altered by reversing the sense of deformation [871]. A careful examination of published micrographs of butterflies sometimes reveals the four wings even when the rolling direction is maintained constant, but with two of the cracks being much smaller than the other pair; see for example, Fig. 6a of [914].
orientations (inset, Fig. 131); on the basis of the shear stresses, two pairs of differently oriented wings are expected. The clue lies in the fact that the wings are always orientated in the direction of ball motion. It is only when a rolling contact fatigue test is interrupted and the direction of rotation reversed, that four-winged butterflies appear as shown in Fig. 130[913]. This suggests a role of deformation history, i.e., the direction of rolling contact; supporting evidence for this conclusion is that the orientation of the www.phase-trans.msm.cam.ac.uk-etching bands (HABs) can appropriately be altered by reversing the sense of deformation [871]. A careful examination of published micrographs of butterflies sometimes reveals the four wings even when the rolling direction is maintained constant, but with two of the cracks being much smaller than the other pair; see for example, Fig. 6a of [914].
|
(a)
![\includegraphics[width=0.45\textwidth]{Tricot_1972_a.eps}](img637.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Tricot_1972_b.eps}](img638.png)
|
Each wing has two different kinds of interfaces with the steel; the first is rather straight and has parallel cracks in its vicinity. The second interface, on the opposite side of the wing, has a diffuse and wavy interface. There is a variation in grain size across the wing; the size is 10-50nm in the vicinity of the major crack, increasing to about 100nm towards the wavy interface [911] perhaps indicating a gradient of plastic strain. Contained within the wing are a number of defects other than the microcracks, including tiny voids, ultrafine grains and fragmented cementite particles. The cementite may be completely absent, having dissolved within the matrix as dislocations and interfaces generated by the deformation are better sinks for carbon [915, 834]. The finer cementite resulting from martensite tempering, as opposed to the proeutectoid cementite, dissolves readily [916]. The phenomenon of cementite dissolution during heavy deformation has been widely studied [917] and several other mechanisms may act simultaneously, for example, the creation of slip steps on the cementite which reduce its thermodynamic stability [918, 912]. That the White matter associated with cracks and butterflies is supersaturated with carbon was shown by Loy and McCallum [909] who discovered fine precipitation in the www.phase-trans.msm.cam.ac.uk layers following a tempering heat treatment; the intensity of precipitation was so large that the hardness increased slightly, and the tempered www.phase-trans.msm.cam.ac.uk layers then appeared darker than the surrounding overtempered martensitic matrix. 24
![\includegraphics[width=0.8\linewidth]{wings.eps}](img639.png)
|
Hard White matter contains cracks, and when two such cracks are parallel, the shearing action of rolling contact causes fragmentation of the intervening matrix. Since this occurs beneath the surface of the steel, the fragments can become rolled into spheres of White matter as illustrated in Fig. 132.
![\includegraphics[width=0.98\linewidth]{spheres_Loy.eps}](img640.png) |
The 1C-1.5Cr (52100) bearing steel has been observed to show very large www.phase-trans.msm.cam.ac.uk-etching bands on the scale of the billets in their continuously cast state [919]. The bands are caused by a redistribution of heterogeneous liquid due to electromagnetic stirring during continuous casting, the mechanism for which is not understood, but which leads to the formation of a carbon-depleted zone some distance from the centre of the casting, Fig. 133.
![\includegraphics[width=0.98\linewidth]{Zhou.eps}](img641.png) |
The term `creep' is used here in a general sense where thermally activated deformation occurs as a function of time at stresses below the yield strength as measured in a tensile test. The observed strain is not necessarily associated with the diffusion of large atoms or dislocation climb. The process might be described better as relaxation.
Creep at low homologous temperatures is thermally activated and attributed to two possible mechanisms: (i) dislocation glide; (ii) time-dependent phase transformation or twinning plasticity. In the former case, the strain increases logarithmically with time and the involves either the work-hardening of barriers to dislocation glide, or the gradual exhaustion of weaker barriers [920].
The second mechanism is a consequence of transformation strains [921], due for example to the volume change accompanying the change in crystal structure, or shear strains due to displacive transformations. The strain still varies with the logarithm of time and is thermally activated, but the time-dependence of phase transformation can be less clear at the low homologous temperatures involved. It has been suggested, although there is little direct evidence, that in 52100 steel which is quenched and tempered 25 , the coarsening of transition carbides of iron leads to plasticity involving the diffusion of carbon atoms from dissolving to growing particles [922]. The leads to a logarithmic variation in strain with time although the details are not established. It is feasible, however, that coarsening occurring under the influence of an external stress may lead to a Greenwood-Johnson type [923] transformation plasticity effect which manifests as time-dependent creep. The strain recorded is very small indeed, Fig. 134.
![\includegraphics[width=0.98\linewidth]{Morra.eps}](img643.png) |
The term `through hardening' implies that the entire component is produced in the martensitic state. This may not be necessary in large components where the heavily loaded regions form a small fraction of the body of the material. Untempered high-carbon martensitic steels can achieve a maximum hardness of about 800 HV [223] but the dissolved carbon tends to make the martensite brittle. One solution is to use a low-carbon steel but to diffuse a larger concentration into the surface which is then transformed into hard martensite, in a process known as case-hardening. This typically gives a strong, wear-resistant layer with a hardness of about 750 HV [925, 924], but the surface itself still lacks ductility. The limiting factor is in fact the static load carrying capacity. Nevertheless, having a tough, unhardened core supporting the working volume of the bearing raceway has advantages, and in some cases hybrid bearings with ceramic rollers running on case-hardened raceways outperform through-hardened steel versions [601].
It is worth emphasising that the case and its mechanical property profile must be designed so that a hardness of about 60 HRC is maintained to beyond the depth where the stresses which do the greatest damage occur [284]. Fig. 135illustrates that a Hertzian pressure of 4000 MPa could not be tolerated given the strength profile produced in a case-hardened bearing steel.
![\includegraphics[width=0.98\linewidth]{Bohmer_carburise.eps}](img644.png) |
Case-hardening has an advantage in the context of bearings because it results in the development of compressive stresses which extend at least to the depth of the case. This is because the martensite-start temperature of the carbon-rich case is lower than that of the core steel. The latter therefore transforms first on cooling, and the associated transformation strain (expansion) causes the case which is still austenitic, to relax by plastic deformation. On subsequent transformation into martensite, the expansion of the case is constrained by the bulk of the core, leading to the compressive stresses, Fig. 136. It is said that the magnitude of the compressive stress is a function of the difference in the martensite-start temperatures of the case and core [161].
The stress profiles can be modified dramatically if large fractions of retained austenite persist in the case, since as already noted, it is the martensitic transformation strain that is the cause of the compressive stresses. It is not then surprising that steps taken to transform the retained austenite in carburised or carbonitrided cases lead to enhanced fatigue properties [926].
Averbach and co-workers [343, 561] undertook experiments in which both M50 NiL and CBS 1000M were carburised to a depth of 2.5mm, which is larger than the work reported in [324]. Fig. 137shows the distribution of residual stress as a function of depth for these two steels after carburising, austenitisation, and repeated refrigeration and tempering. It is noticeable when comparing against Fig. 136that the depth of carburising has significantly altered the retained austenite content and hence the stress distribution, with smaller compressive stresses in both alloys, and worrying tensile stresses in the close proximity of the surface of the M50 NiL. These comparisons might indicate that deep decarburisation of these aeroengine bearing steels is not optimum for the development of favourable stresses in the case.
Averbach's results are extraordinary in another respect. They imply that the retained austenite within the case carburised regions of M50 NiL and CBS 1000M is incredibly resistant to some quite severe and multiple tempering and refrigeration heat treatments. It can be shown using phase stability calculations [41] that at the tempering temperature of 510 ![]() C, M50 NiL containing 1.15 wt% of carbon representative of the carburised surface, will contain austenite as an equilibriumphase in addition to ferrite,
C, M50 NiL containing 1.15 wt% of carbon representative of the carburised surface, will contain austenite as an equilibriumphase in addition to ferrite, ![]() ,
, ![]() ,
, ![]() and
and ![]() . However, the amount of equilibrium austenite is only about 3% and cementite is not predicted exist (a similar calculation done in 1990 showed the absence of equilibrium austenite [326]). It is evident therefore that the large quantities of austenite observed cannot ultimately be stable, but that the heat treatment required to achieve equilibrium must be impractically long. Any equilibrium austenite would contain some 50 wt% of nickel and that would necessitate considerable diffusion to achieve.
. However, the amount of equilibrium austenite is only about 3% and cementite is not predicted exist (a similar calculation done in 1990 showed the absence of equilibrium austenite [326]). It is evident therefore that the large quantities of austenite observed cannot ultimately be stable, but that the heat treatment required to achieve equilibrium must be impractically long. Any equilibrium austenite would contain some 50 wt% of nickel and that would necessitate considerable diffusion to achieve.
![\includegraphics[width=0.98\linewidth]{Wensing2.eps}](img646.png) |
|
(a)
![\includegraphics[width=0.45\textwidth]{Averbach_stress.eps}](img647.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Averbach_austenite.eps}](img648.png)
|
Although not in the context of bearing steels, case-carburised steel isothermally transformed at 200 ![]() C has been shown to lead to extremely fine and hard bainite (620 HV) in the surface layer, with the transformation inducing a compressive stress of about 200 MPa into the surface [927]. The rolling contact fatigue resistance of bearing rings with this treatment has also been shown to be superior to that of tempered martensite [928]. Similar results have been claimed for bainitic cases produced at higher temperatures; it seems that the distortion associated with the production of the bainitic case is smaller than with the martensitic variety because of the less dramatic quench to the isothermal transformation temperature [929].
C has been shown to lead to extremely fine and hard bainite (620 HV) in the surface layer, with the transformation inducing a compressive stress of about 200 MPa into the surface [927]. The rolling contact fatigue resistance of bearing rings with this treatment has also been shown to be superior to that of tempered martensite [928]. Similar results have been claimed for bainitic cases produced at higher temperatures; it seems that the distortion associated with the production of the bainitic case is smaller than with the martensitic variety because of the less dramatic quench to the isothermal transformation temperature [929].
The dry sliding-friction wear resistance of nanostructured bainite has been reported in [930] who found that the austenite in the vicinity of the friction surface decomposes under the influence of shear strain, resulting in the formation of an even finer structure with grains of ferrite only a few nanometers in size. It was suggested that these events play a role in determining the wear resistance, which is comparable to that of quenched and tempered martensitic structures. This augers well for the development of case-hardening technology based on the nanostructured bainite [932, 931].
One of the criteria necessary to ensure an adequate case depth has already been described in the context of carburisation, that it must include the zone which is most susceptible to damage by Hertzian stresses [284]. An inadequate case-depth obviously will lead to plasticity within the softer substrate which as a consequence is less able to support the case which is bent by the load and may therefore crack due to tensile stresses developed in the case in the radial direction (normal to the raceway surface).
Lai and coworkers [933] have developed a method for assessing the adequacy of the hardened layer with respect to indentation and sub-surface fatigue damage arising from the repeated application of load at the same location on the raceway, a process known as standing contact fatigue. First, the depth to which a material becomes indented is given by:
 |
(42) |
For a case-hardened surface,
The second stage is the calculation of the critical alternating stress ![]() during static fatigue, which allows a pre-existing penny-shaped crack of size
during static fatigue, which allows a pre-existing penny-shaped crack of size ![]() , located at the case-core interface, to grow by fatigue, taking account of short-crack fracture mechanics theory 26 :
, located at the case-core interface, to grow by fatigue, taking account of short-crack fracture mechanics theory 26 :
 |
(44) |
![\includegraphics[width=0.98\linewidth]{case_depth.eps}](img661.png) |
| < /td> |
The radius of wind turbine blades has increased from 5 to 70 metres over the past 25years resulting in an increase in power output to about 10MW [934]. The rotation rate of the blades is such as to keep the tip velocity below that of sound in air, so mills with large blades must rotate slowly. The slow turning motion of the blades is transmitted to a gearbox via a main shaft that is supported on large bearings, Fig. 139. The purpose of the gearbox is to increase the rotation rate of the shaft (25-35 r.p.m.) connecting to the electricity generator to some 1500-1800 r.p.m. in order to comply with electrical grid requirements. The assembly is contained in a pod often referred to as a nacelle. The pod in turn is connected to the windmill tower by a yaw bearing which allows it to turn about the vertical axis. The blades themselves are connected via bearings to the main shaft in order to provide additional degrees of freedom to set the pitch of blades, for example to minimise blade loads during storms or to take maximum advantage of wind conditions. Since the torque on the shaft scales with the cube of the radius (blade size), it is obvious that demands on gear boxes and bearings increase dramatically and these technologies do not seem to have kept pace with the perceived windmill life of 20years.
![\includegraphics[width=0.98\linewidth]{windmill.eps}](img662.png) |
In excess of 60% of gearbox failures are attributed to bearings; although such failures are much less frequent than those associated with electrical components, they are much more expensive to repair [935]. There is no clear consensus on the cause of these bearing failures, other than the usual phenomena being mooted as possible culprits: subsurface www.phase-trans.msm.cam.ac.uk-etching cracks and hydrogen. Additional phenomena include rapid and sometimes stochastic loading together with turbulent wind flow patterns. Bearing steels in windmills are susceptible to microbial attack, erosion and corrosion; these issues are handled through sealing systems rather than by utilising expensive materials which resist these phenomena.
Yaw and pitch bearings are case-hardened to about 58 HRC or induction-hardened to some 56 HRC; the core hardness of the medium carbon steels used is about 50 HRC [935]. A change in raceway hardness from 58 to 56 HRC can reduce the ![]() life by 30% [935, 936]. The depth and strength of the surface-hardened region, and core properties, also feature in the integrity of the bearing when the windmill is not operating because the raceways are then subjected to static loads and vibrations, which can lead to deformation and metal-to-metal contact as lubricant is squeezed out. The grooves that form at the points of contact then are subjected to further damage during operation, leading to the so-called false brinelling as illustrated in Fig. 140.
life by 30% [935, 936]. The depth and strength of the surface-hardened region, and core properties, also feature in the integrity of the bearing when the windmill is not operating because the raceways are then subjected to static loads and vibrations, which can lead to deformation and metal-to-metal contact as lubricant is squeezed out. The grooves that form at the points of contact then are subjected to further damage during operation, leading to the so-called false brinelling as illustrated in Fig. 140.
![\includegraphics[width=0.98\linewidth]{Kotzalas_3.eps}](img663.png) |
The main shaft is usually supported by spherical roller bearings because of they can cope with both axial and radial loads and to accommodate shaft misalignment. Experience in the wind turbine industry suggests that these bearings in particular suffer from early failure, i.e.much earlier than say the ![]() life. Some of the failures are attributed to damage from wear which leads to micropitting [935]. Work on carburised gear steels indicates that the key factors other than material type, influencing the development of micropits contact experiments, are surface finish, lubricant, load, temperature, speed and slide-to-roll ratio; the last two have the greatest effect on pit propagation whereas the load is most responsible for initiation [937].
life. Some of the failures are attributed to damage from wear which leads to micropitting [935]. Work on carburised gear steels indicates that the key factors other than material type, influencing the development of micropits contact experiments, are surface finish, lubricant, load, temperature, speed and slide-to-roll ratio; the last two have the greatest effect on pit propagation whereas the load is most responsible for initiation [937].
Fig. 141a shows the initial stages of such damage with two distinct wear tracks forming on the raceway. The stress concentrations resulting from the microscopic pits in this region then lead to fatigue spalling as illustrated in Fig. 141b. There is evidence that this kind of damage begins with sliding shear as opposed to rolling contact, between the rollers and raceway [935]. If this is the cause for most early failures then the solution lies in engineering design rather than material improvements. Early work on the theory of micropitting suggests that there are three parameters which significantly influence the development of these pits [938]. The first is the contact area between the raceway and rolling element, the distance between asperities and the Stribeck parameter ![]() which is the ratio of the lubrication film thickness to composite surface roughness (section 27). Pitting is diminished when the asperities are deformed elastically during the operation of the bearing.
which is the ratio of the lubrication film thickness to composite surface roughness (section 27). Pitting is diminished when the asperities are deformed elastically during the operation of the bearing.
|
(a)
![\includegraphics[width=0.45\textwidth]{Kotzalas_1.eps}](img664.png) (b) (b) ![\includegraphics[width=0.45\textwidth]{Kotzalas_2.eps}](img665.png)
|
One problem with large bearing rings, such as those associated with wind turbines, is that the amount of deformation the steel experiences between the casting and the final assembly is necessarily limited. The deformation, in addition to producing the required shape, is useful in refining the structure, enhancing chemical homogeneity and breaking up inclusions. The role of deformation processing on inclusions is well-known, but recent work confirms this in the context of modern 52100 type steel, where the oxysulphide inclusions were characterised using the statistics of extreme values, and the ![]() life was shown to vary by approximately an order of magnitude as a function of the reduction ratio [939]. One solution proposed a long time ago, is to use deformed strip which is profile rolled into circular form and butt-welded [940]. However, there are no details available and the process does not seem to have been adopted.
life was shown to vary by approximately an order of magnitude as a function of the reduction ratio [939]. One solution proposed a long time ago, is to use deformed strip which is profile rolled into circular form and butt-welded [940]. However, there are no details available and the process does not seem to have been adopted.
The purpose here is not to reflect conclusions or derived concepts which have been stated in context, but rather, to highlight a few of the interpretations which may be helpful in defining progress or in encouraging discussion:
I am grateful to Professor Lindsay Greer for the provision of laboratory facilities at the University of Cambridge, and to support from the World Class University Programme of the National Research Foundation of Korea, Ministry of Education, Science and Technology, project number R32-10147.
I am especially grateful to John Beswick for giving me access to his enormous library of literature on bearings, for addressing my occasional queries, and for thorough, constructive comments on a draft of this manuscript. Many colleagues, and sometimes those with whom I had no prior contact, have been generous in providing me with publications and micrographs, which I have acknowledged in the body of the text. I had interesting discussions with Professors Dong Woo Suh and Nagraj Arakere.
For the vast majority of engineering applications, bearing steels are designed on the assumption that the component in service will be reasonably well-lubricated. It is only then that rolling contact fatigue, inclusions and internal defects determine life. If surface damage due to sliding or gross plasticity resulting from inadequate strength become prominent then defects such as those defined by inclusions become less important in initiating failure [947].
The Stribeck curve [38] defines three regimes of friction during lubricated rolling contact. The curve relates the friction coefficient defined as the ratio of the normal force ![]() Normal force
Normal force ![]() to the force of kinetic friction
to the force of kinetic friction ![]() Force of kinetic friction
Force of kinetic friction ![]() , to the ratio
, to the ratio ![]() Ratio of lubricant film thickness to metal roughness
Ratio of lubricant film thickness to metal roughness ![]() of the lubricant film thickness to metal roughness, as illustrated in Fig. 142;
of the lubricant film thickness to metal roughness, as illustrated in Fig. 142; ![]() is sometimes called the specific film thickness ratio, and gives an indication of the efficacy of the lubricating film:
is sometimes called the specific film thickness ratio, and gives an indication of the efficacy of the lubricating film:
The viscosity is not a fixed parameter because the lubricant comes under intense pressure between the elastically-deformed rolling body and substrate, which increases its viscosity and retains it in position rather than the fluid being squeezed out by the pressure. This phenomenon, known as elastohydrodynamic lubrication, is more effective at high rolling speeds. This is why the rolling contact fatigue life of 52100 steel improves as the revolutions per minute increase from 10,000 to 50,000 in the presence of appropriate lubricants [952].
The solids come into partial contact in regime I where the roughness of the metal surface exceeds the thickness of the lubricant film ( ![]() ). As a result, the friction coefficient is large leading to significant microscopic deformation at the points of metal to metal contact.
). As a result, the friction coefficient is large leading to significant microscopic deformation at the points of metal to metal contact.
In regime II, ![]() describes the case where metal to metal contact still occurs but to a much smaller extent than in regime I.
describes the case where metal to metal contact still occurs but to a much smaller extent than in regime I.
Regime III corresponds to the case where metal to metal contact is avoided and the friction coefficient is determined by the properties of the lubricant (for example, its viscosity) and the relative speed of the metallic components.
As an example, at a maximum Hertzian stress of 4800 MPa, when the rolling speed is changed from 12.5 to 25.0ms ![]() ,
, ![]() Changes from 1.48 to 2.48 and the
Changes from 1.48 to 2.48 and the ![]() fatigue life increases from 7.4 to 26.9 million cycles for an M50 steel bearing [951].
fatigue life increases from 7.4 to 26.9 million cycles for an M50 steel bearing [951].
 |
| PT Group Home | Materials Algorithms |